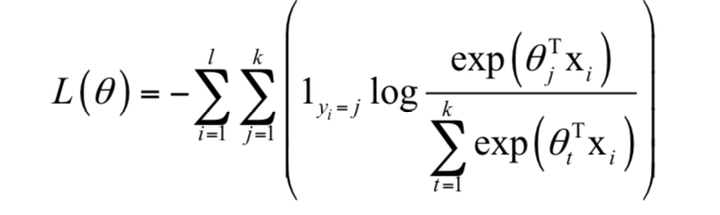凸优化是优化中比较容易的一种

优化optimization，即数学规划。     优化=规划

优化：（包含三个要素）可行解的集合、定义最优、找出

任何一个优化问题，总可以写成这样的形式：

minimize  函数  ，最优的准则

约束：使得 ，    i=1,2,...,M    总共有M个约束。叫做：不等式的约束

    优化变量

 ，    目标函数 、是从n维空间到1维空间的映射

找到最优解   ，

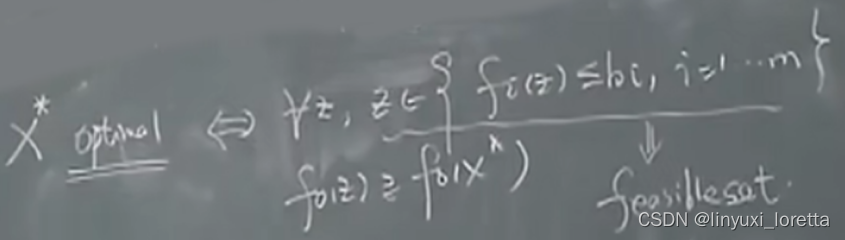
 feasible set可行解集合

目标：minimize objective function——fo（x），

约束为：｜x｜<=a，

可行域feasible set——fi（x）在约束范围内，

最优解x*使得f（x*）<=f（x）

应用：

例子1：数据拟合问题：使得 测量误差最小

min 

      i=1,...,n

例子2：线性二次调节器 LQR。 

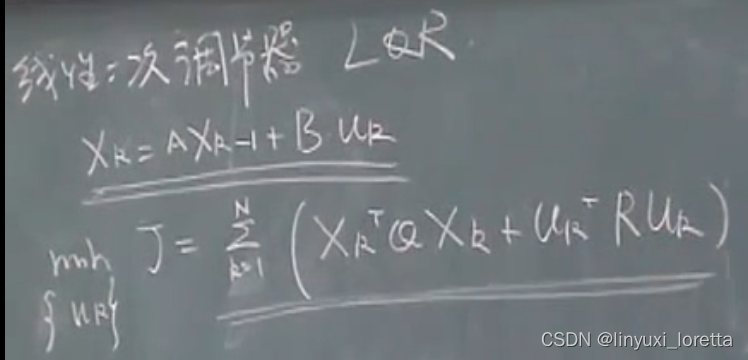
 自动化系。 现代控制理论。

表示系统在k时刻的状态，由k-1时刻的状态，经过状态转移A矩阵、再加上k时刻的输入 、乘以 输入的矩阵B构成。用来描述 离散的动态系统、

卡尔曼滤波只是用了这个线性的模型，从这个式子推出来的，这是马尔科夫状态转移矩阵

RNN

优化控制序列 、通过序列 来调节输出的状态

在 N长的时间段内，min（状态的方差、输入的方程（输入的能量））

动态求解 黎卡提方程，

例子3：多用户的能量控制问题

通信工程系，控制理论，

一组 发送者Tx   ---> 接收者Rx，叫一个用户Ui

用户 Ui 以单位能量Pi来发送信号，对第j个用户产生的干扰   αij

每个通信链路  存在一定噪声 高斯白噪声 每个噪声方差 δi^2   

信干燥比  SINR 

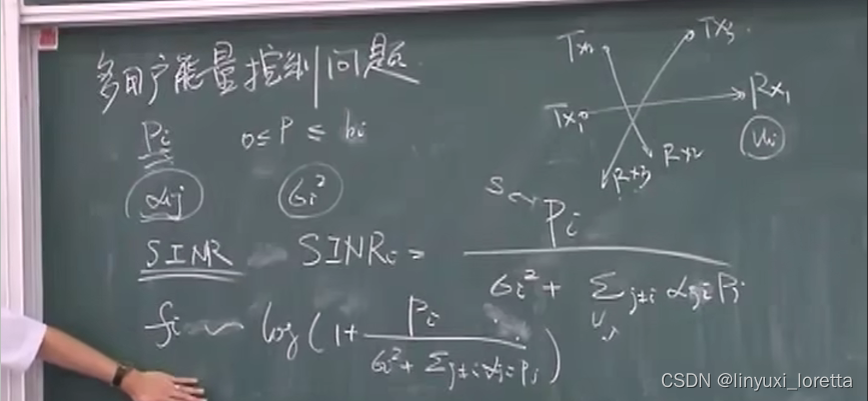
 链路码率和信噪比相关      用户Ui的码率fi（信道容量）

香农定理

电信运用商，希望用户发送的码流尽可能大，信道所通路的信息量尽可能大，赚的多

max 网络的流量   

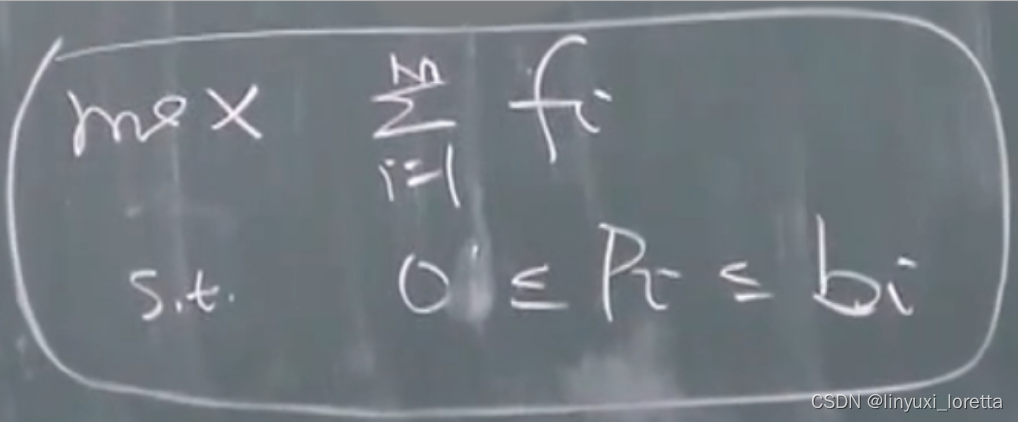
例子4：图像处理：TV-L2模型

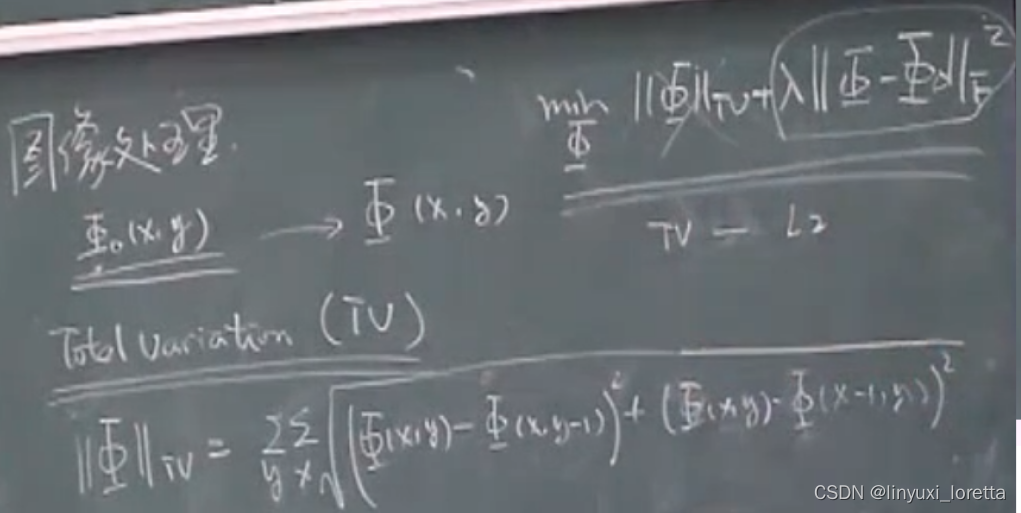
 二维图像 带噪声，恢复出不带噪声的图像

所有自然图像都有一定规律，如 e.分片光滑

照片中会有一些很大的色块，（线性知识、要使得图像 在TV范数意义下 尽可能小，即分片光滑、

 TV范数（总变差）：对图像做两个方向上的差分，平方和 再开根

min 后项为  规范化项  λ可任选、因为还需要Φ 接近Φ0，即 使得两个矩阵之差的F范数尽可能小

F范数   即 矩阵所有元素的平方和 再开根号

例子5：超大规模集成电路设计

23系 电子科学与技术系，

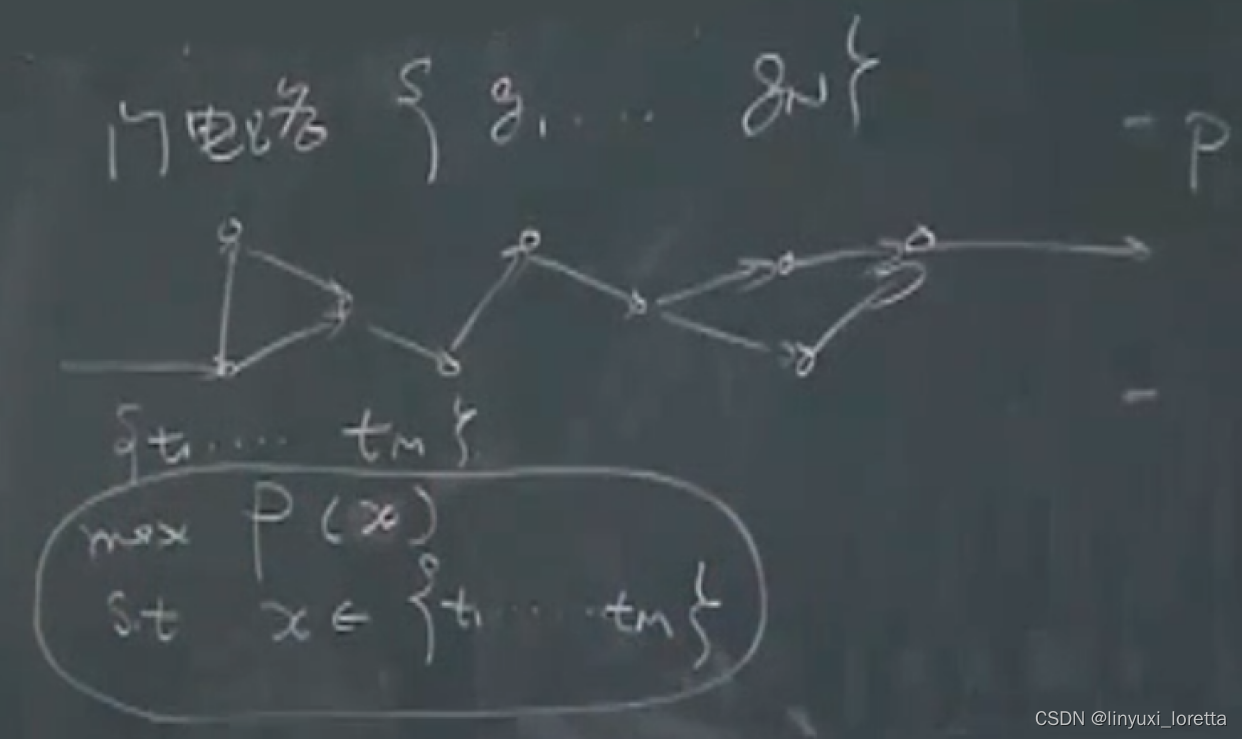
 门电路集合，连成有向图集合，完成一定的功能，有可能的连接t1,...tm

且系统达到一些性能指标（如能耗、资金）P，

这类问题很难，一般都是非凸优问题

例子6：计算机系，最短路径问题

 网络, 如何访问网站花费的代价最小

无向图，顶点、边、边的权重 表示 从第1个点到第2个点所花的代价，

迪杰斯特拉算法、贝尔曼福德算法可解

选择的问题一般都是很难的，

可以把xij =0 or 1，改写 简化成xij>=0， 线性规划（容易）

首先改成大于等于0的目的是为了将选择的问题改成线性规划的问题

放松条件之后你可能得到比如0.9这样的解，说明这个问题整数不能达到目标函数的最优， 然后去看0.9附近哪个整数更优，从而得到整数规划的答案。

优化问题的分类

1. 线性规划；非线性规划

 单纯形法 是 解决线性规划问题的标准方法，

图表示：从f1,...fm的约束，所构成的空间、即 可行解集

因为约束空间的每个函数都是线性函数，可行解集 一定是这样有很多条直线所圈出来的形状

目标函数 也是线性函数，在空间里描述出来，等高线，每条线都是f0的取值

想象 黑板就是x的空间，框出来的是 可行解集    线上的x  对应的f0是相等的，

因为是线性目标函数，所以梯度方向是垂直于等值线的，然后两个方向随意指了一个（？）

2.凸规划/ 非凸规划

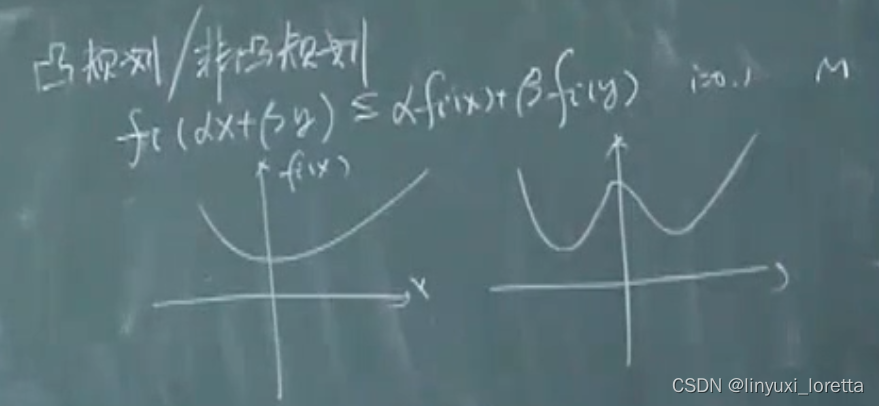
 目标函数是凸函数、可行解集是凸集

凸函数：没法找到一些不相邻的最低的点

任何线性规划问题都是凸规划，易解

3. 光滑/ 非光滑         

一般是针对目标函数f0(x)而言

光滑函数：函数在每个点都是可微的

非光滑 e.g. 折线。     问题稍难，但不是本质差别

4.连续/ 离散

针对可行域而言

e.g. 大规模集成电路   离散点，因为一般来说 都是非凸问题

5. 单目标/ 多目标

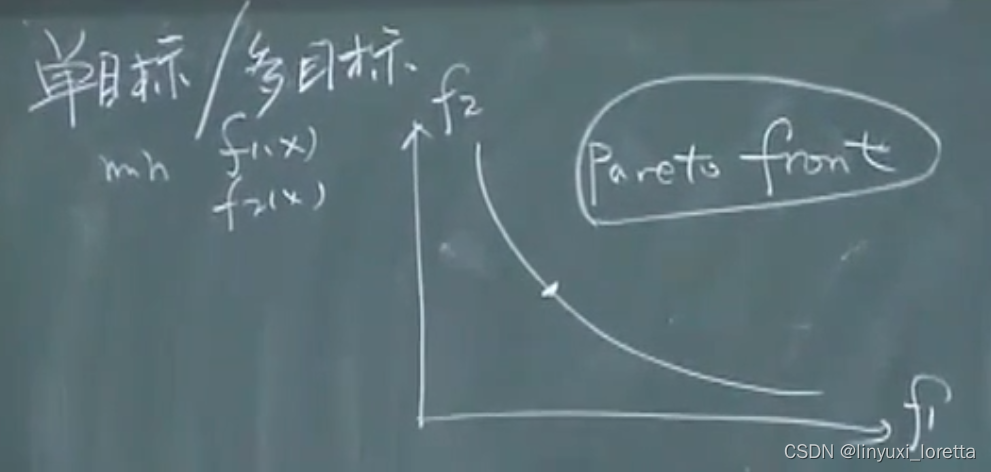
 e.g. 房价调控，政府和人民目标不一样

帕累托曲面，面上所有点 没法找到任意x 使得f1和f2都小，没有“最好的”指标

折中pareto  

多目标优化问题  很多时候可以通过加权成，单目标优化问题

但并不总是管用，因为很多问题，加权不一定能得到帕累托曲面

任何优化问题，如果能变成凸优化问题，相当于完成90%了，

本门课 所指的难： 问题 求解难，而不是指目标函数难以计算

发展历程：

拉格朗日乘子，把约束变成目标。    这节课的重点：找出目标和约束间的关系

1940 贝尔曼动态优化   

有一个 时间序列、需要优化每个点的值、来达到总体目标，可以从后往前来优化，

1944 冯诺依曼 博弈论，每个人都要优化自己的目标函数，区别于多目标优化

纳什均衡

1939  苏联 集体农庄 生产资料调配，线性规划 Kantorovich

1947 单纯形法  

线性规划问题，一定能保证在多项式时间内求解出来、

单纯形法 不能保证，存在问题

改进   1979   内敛法、理论上可行，实际不够好用

1984   内点法IPM、解决大规模线性规划问题 最有效的方法

1990   内点法 拓展到非线性

仿射集affine sets   

 凸集的 特例

仿射包(affine hull)

从c里任意选k点，做仿射组合，从x1,x2集合构造出仿射包，从非仿射集合构建出仿射集合

凸集、

凸包（Convex Hull）   

 计算几何（图形学）中的概念

从非凸集合构造最小凸包

锥 cone 

凸锥 convex cone

锥组合就是“凸+锥“组合。

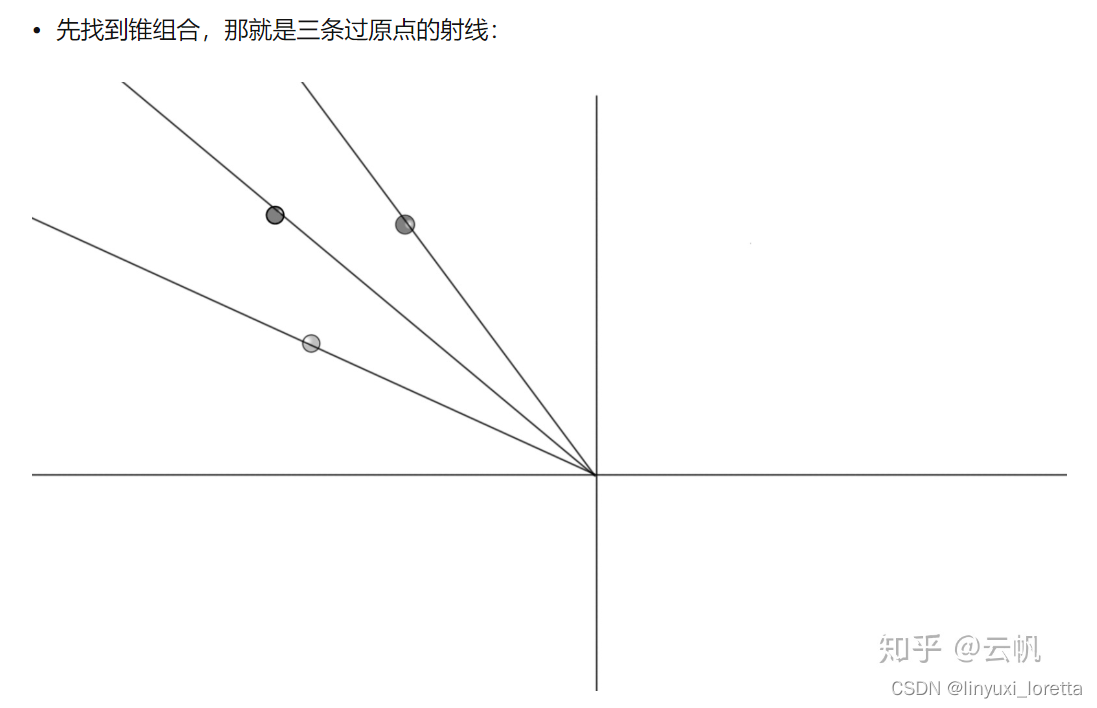
 任意仿射集   一定是凸的；凸锥也一定是凸的

c={x}   也是仿射集       θ1x+θ2x=x     是凸集；除非是原点，否则不是凸锥

空集    是 仿射集、凸集、也是凸锥(集)

R^n空间、R^n空间的子空间     是 仿射集、凸集、也是凸锥

超平面与半空间

超平面是个集合，

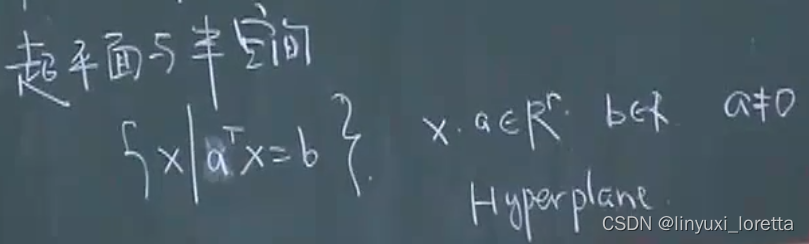
线性方程  a^T x=b  、的解集 

典型的凸集

球和椭球

Euclidean欧几里得空间，指的是 我们能使用  2 norm     

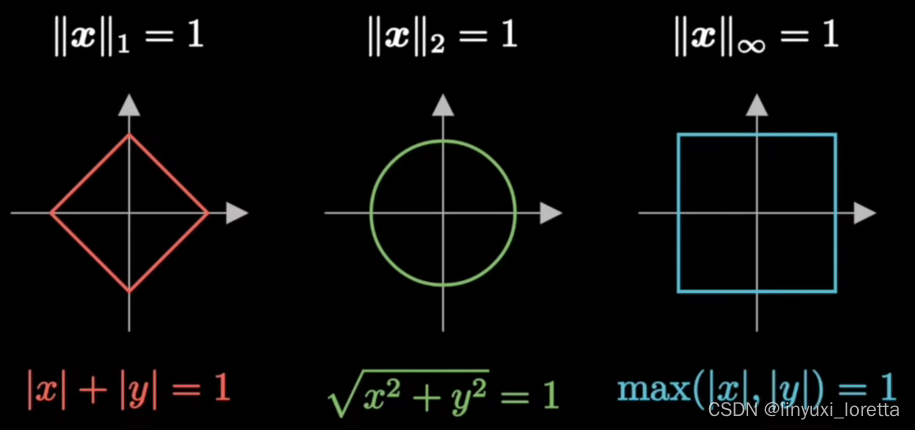
补充知识：范数

向量的【范数】：模长的推广，柯西不等式_哔哩哔哩_bilibili

 【范数】：模长的推广

范数可以定义在任何线性空间上

 p范数

||x||2   也就是平时用的模长、也叫欧几里得范数、欧式范数、是现实世界中的长度

||x||1   出租车/ 曼哈顿范数。长度定义成 沿着道路走过的距离

2范数的性质： 酉变换下保持不变

酉矩阵  实数域中是正交阵

说白了就是正交变换，扩展到复数域了

 正交变换是保持长度的，也被称作刚体变换

三角不等式定理：||a+b||<= ||a||+||b||      对于任意范数

任意两边之和 ≥ 第三边

(x-xc)^T P^-1 (x-xc)     加权的二范数。      通过 P^-1 来加权

补充知识：奇异值

A^T A   一定是方阵、对称。他的特征值一定都是>=0，

     即矩阵A的奇异值

方阵的奇异值和特征值也是可能不一样的。   

但是对于 特殊的一些方阵，如   奇异值和特征值一样

多面体、有界多面体

 一系列的半空间和超平面的交集、

多面体不一定都有界，如：只有一个半空间的约束

多面体是凸集

单纯形 simplex 

单纯形是代数拓扑中最基本的概念。单纯形是三角形和四面体的一种泛化,一个k维单纯形是指包含 k+1个节点的凸多面体。

单纯形  一定是个多面体

对称矩阵、半正定矩阵、正定矩阵、

  是凸锥、  对称的矩阵集合是 凸锥、对称正定  不是凸锥

矩阵空间和实数空间对应来考虑

仿射函数

 仿射，即 线性的映射 

f是从n维空间到m维空间的映射

x是n维空间里的点

凸集经过仿射函数的变换，仍在凸集

拉伸、旋转，线性变化不改变凸性

逆的仿射映射

n维空间里的集合 s、   s中的元素都是通过f(x)得到的，其中x属于k维空间

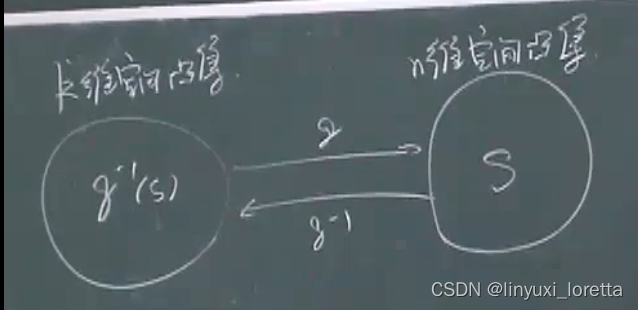
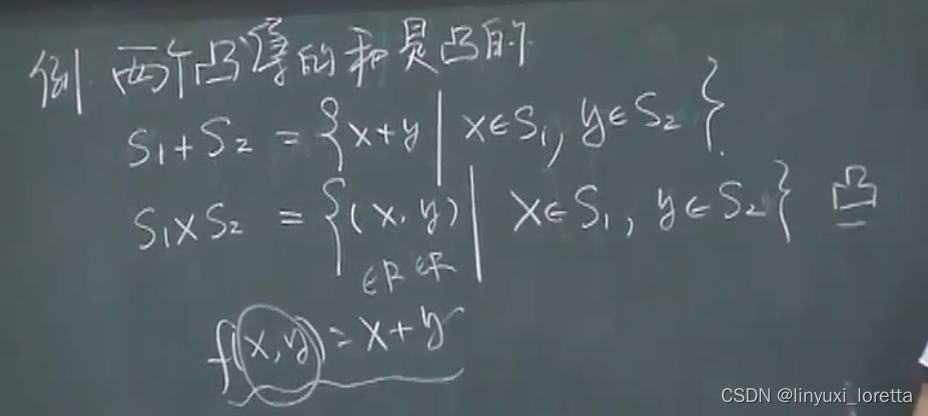
控制里的重要概念，

Ai、Xi对称矩阵

线性矩阵不等式的解集是凸集

-------Lec.07   34:10   --------

Lec11     凸函数定义：

1.  e.g. 锅上的棍子

高维用起来不方便

2. e.g.切西瓜

3.

4.

中科大-凸优化_哔哩哔哩_bilibili

2011年，中科大，凌青的凸优化

全程在板书、在证明定理、在搞定义，传统数学课，听不下去了，  

[凸优化-中文字幕]Boyd斯坦福公开课_哔哩哔哩_bilibili

国内似乎很多学校都用的这老师的书做教材，算是鼻祖把，但是这课上的，非常不国外风格，第二课直接扑面而来一大堆概念，机翻都不知道说的啥概念，记了一脑袋英文专业名词。