总结自:机器学习(李宏毅,台湾大学)
上一篇文章中,我们选用的model是 y = b + w ∙ x c p y=b+w \bullet x_{cp} y=b+w∙xcp,可以选用其它的model吗?我们选用的loss function是 L ( f ) = ∑ ( ( y ^ ) n − y n ) 2 L(f)=\sum((\hat{y})^n - y^n)^2 L(f)=∑((y^)n−yn)2,可以选用其它的loss function来计算函数的优度吗。如果我们选用其它的model,选用其它的loss function,预测结果是会更好还是更坏呢?
1. Model Selection
1. 越复杂的model越好?
前文提到,我们选择的model是 y = b + w ∙ x c p y=b+w \bullet x_{cp} y=b+w∙xcp ,最后挑选出来的函数 f ∗ f^* f∗ 计算得出的Training Error 是31.9,而Testing Error是35.0。接下来我们思考,如果选用的model是 y = b + w 1 ∙ x c p + w 2 ∙ ( x c p ) 2 y=b+w_1 \bullet x_{cp}+w_2 \bullet (x_{cp})^2 y=b+w1∙xcp+w2∙(xcp)2 或者更复杂的model呢?
我们选择以下5个model:
- y = b + w ∙ x c p y=b+w \bullet x_{cp} y=b+w∙xcp
- y = b + w 1 ∙ x c p + w 2 ∙ ( x c p ) 2 y=b+w_1 \bullet x_{cp}+w_2 \bullet (x_{cp})^2 y=b+w1∙xcp+w2∙(xcp)2
- y = b + w 1 ∙ x c p + w 2 ∙ ( x c p ) 2 + w 3 ∙ ( x c p ) 3 y=b+w_1 \bullet x_{cp}+w_2 \bullet (x_{cp})^2+w_3 \bullet (x_{cp})^3 y=b+w1∙xcp+w2∙(xcp)2+w3∙(xcp)3
- y = b + w 1 ∙ x c p + w 2 ∙ ( x c p ) 2 + w 3 ∙ ( x c p ) 3 + w 4 ∙ ( x c p ) 4 y=b+w_1 \bullet x_{cp}+w_2 \bullet (x_{cp})^2+w_3 \bullet (x_{cp})^3 + w_4 \bullet (x_{cp})^4 y=b+w1∙xcp+w2∙(xcp)2+w3∙(xcp)3+w4∙(xcp)4
- y = b + w 1 ∙ x c p + w 2 ∙ ( x c p ) 2 + w 3 ∙ ( x c p ) 3 + w 4 ∙ ( x c p ) 4 + w 5 ∙ ( x c p ) 5 y=b+w_1 \bullet x_{cp}+w_2 \bullet (x_{cp})^2+w_3 \bullet (x_{cp})^3 + w_4 \bullet (x_{cp})^4 + w_5 \bullet (x_{cp})^5 y=b+w1∙xcp+w2∙(xcp)2+w3∙(xcp)3+w4∙(xcp)4+w5∙(xcp)5
这5个Model在Training Data上的表现如下:

我们可以看到越复杂的model在Training Data上的表现越好1,因为上述复杂的model其中就包含简单的model2。
然而,我们关心的并不是函数在Training Data上的表现,我们更关心函数在新的数据Testing Data上面的表现。

上图是不同model找到的 f ∗ f^* f∗ 在Training Data和Testing Data上的表现。越复杂的model在Training Data上的表现越好,而在Testing Data上则不一定。甚至在model 5中,找到的 f ∗ f^* f∗ 在Testing Data上的Average Error不降反升,达到了100。我们称之为overfitting(过拟合)。
所以在选择model的时候,并非越复杂越好,我们应该选择最适合的model。
2. 其它属性对预测值有无影响?
再回顾之前我们一开始用的model, y = b + w ∙ x c p y=b+w \bullet x_{cp} y=b+w∙xcp,我们只考虑了宝可梦进化前的CP值 x c p x_{cp} xcp去预测进化后的CP值,而宝可梦还有一些其它的属性,例如: x s x_s xs, x h p x_{hp} xhp, x w x_w xw, x h x_h xh(种类,血量,重量,高度),这些属性会影响我们对CP值的预测吗?
我们先收集更多的数据看看:

2.1. 种类对预测值的影响
接下来,我们考虑一下不同种类的宝可梦。
- 如果这只宝可梦的种类是Pidgey,即 x s = P i d g e y x_s=Pidgey xs=Pidgey ,我们选用的预测函数 f ∗ : y = b 1 + w 1 ∙ x c p f^*:y=b_1+w_1 \bullet x_{cp} f∗:y=b1+w1∙xcp 。
- 如果宝可梦的种类是Weedle,即 x s = W e e d l e x_s=Weedle xs=Weedle ,我们选用的预测函数 f ∗ : y = b 2 + w 2 ∙ x c p f^*:y=b_2+w_2 \bullet x_{cp} f∗:y=b2+w2∙xcp 。
- ……
上述操作仍可用Linear Function表示出来:
y = b 1 ∙ δ ( x s = P i d g e y ) + w 1 ∙ δ ( x s = P i d g e y ) ∙ x c p + b 2 ∙ δ ( x s = W e e d l e ) + w 2 ∙ δ ( x s = W e e d l e ) ∙ x c p + … … y=b_1 \bullet \delta (x_s=Pidgey) + w_1 \bullet \delta (x_s=Pidgey) \bullet x_{cp} +b_2 \bullet \delta (x_s=Weedle) + w_2 \bullet \delta (x_s=Weedle) \bullet x_{cp}+…… y=b1∙δ(xs=Pidgey)+w1∙δ(xs=Pidgey)∙xcp+b2∙δ(xs=Weedle)+w2∙δ(xs=Weedle)∙xcp+……3
不同种类的宝可梦进化后CP值预测的函数图像如下:

计算得出在Training Data上的Average Error是3.8,在Training Data上的Average Error是14.3。这显然是优于我们一开始只考虑进化前CP值的model的。
2.2. 其它属性对预测值的影响
我们接着考虑宝可梦的血量,高度,重量对预测值的影响。
我们重新回到Step 1选择model,这次我们构建了以下model:
y = y ′ + w 9 ∙ x h p + w 10 ∙ ( x h p ) 2 + w 11 ∙ x h + w 12 ∙ ( x h ) 2 + w 13 ∙ x w + w 14 ∙ ( x w ) 2 y=y'+ w_9 \bullet x_{hp}+w_{10} \bullet (x_{hp})^2+w_{11} \bullet x_h +w_{12} \bullet (x_h)^2 + w_{13} \bullet x_w + w_{14} \bullet (x_w)^2 y=y′+w9∙xhp+w10∙(xhp)2+w11∙xh+w12∙(xh)2+w13∙xw+w14∙(xw)2。
其中 y ′ = { b 1 + w 1 ∙ x c p + w 5 ∙ ( x c p ) 2 , I f x s = P i d g e y b 2 + w 2 ∙ x c p + w 6 ∙ ( x c p ) 2 , I f x s = W e d d l e b 3 + w 3 ∙ x c p + w 7 ∙ ( x c p ) 2 , I f x s = C a t e r p i e b 4 + w 4 ∙ x c p + w 8 ∙ ( x c p ) 2 , I f x s = E e v e e y'=\left \{ \begin{aligned} b_1+w_1 \bullet x_{cp}+w_5 \bullet (x_{cp})^2,& If \ x_s=Pidgey \\ b_2+w_2 \bullet x_{cp}+w_6 \bullet (x_{cp})^2,& If \ x_s=Weddle\\ b_3+w_3 \bullet x_{cp}+w_7 \bullet (x_{cp})^2,& If \ x_s=Caterpie\\ b_4+w_4 \bullet x_{cp}+w_8 \bullet (x_{cp})^2,& If \ x_s=Eevee \end{aligned} \right. y′=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧b1+w1∙xcp+w5∙(xcp)2,b2+w2∙xcp+w6∙(xcp)2,b3+w3∙xcp+w7∙(xcp)2,b4+w4∙xcp+w8∙(xcp)2,If xs=PidgeyIf xs=WeddleIf xs=CaterpieIf xs=Eevee
接着计算Training Error和Testing Error,得到Training Error=1.9,Testing Error=102.3。可以看到,这个Testing Error是比较大的,这里又overfitting了。因此,并非考虑的属性越多,得到的预测函数越好。
2. Regularization(正则化)
先看原来我们用的Loss function, L ( f ) = F ( w , b ) = ∑ ( ( y ^ ) n − y n ) 2 = ∑ ( ( y ^ ) n − ( b + ∑ w i ∙ x i ) ) 2 L(f)=F(w,b)=\sum ((\hat{y})^n-y^n)^2=\sum ((\hat{y})^n-(b+\sum w_i \bullet x_i))^2 L(f)=F(w,b)=∑((y^)n−yn)2=∑((y^)n−(b+∑wi∙xi))2 。这个Loss function只考虑了预测结果 y y y产生的Error。
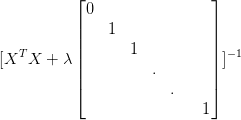
接下来redesign我们的Loss function,即Regularization(正则化),使 L ( f ) = ∑ ( ( y ^ ) n − ( b + ∑ w i ∙ x i ) ) 2 + λ ∙ ∑ ( w i ) 2 L(f)=\sum ((\hat{y})^n-(b+\sum w_i \bullet x_i))^2+ \lambda \bullet \sum(w_i)^2 L(f)=∑((y^)n−(b+∑wi∙xi))2+λ∙∑(wi)2。 λ \lambda λ 是一个常数,需要我们接下来去手调。 λ ∙ ∑ ( w i ) 2 \lambda \bullet \sum(w_i)^2 λ∙∑(wi)2这一项表明我们期待函数 f ∗ f^* f∗拥有更小的 w i w_i wi。 w i w_i wi越小,函数 f ∗ f^* f∗越平滑4。5
我们来看一下Regularization后找到的函数 f ∗ f^* f∗的表现:

当前我们的Loss函数考虑了两项,一项是Error,一项是smooth。 λ \lambda λ越大,考虑Training Error 这一项越少,考虑smooth这一项越多,表示找到的函数 f ∗ f^* f∗越平滑。
我们可以看到 λ \lambda λ越大,在Training Data上得到的Average Error越大6,而在Testing Data上得到的Average Error是先慢慢减小,随后又增大。这表明,虽然我们倾向于找到平滑的 f ∗ f^* f∗,但是也不能太平滑。我们可以通过调整 λ \lambda λ来决定function的平滑程度,从而得到一个最好的model。
表现越好在这里指Average Error更小。这里用来计算Average Error的函数是不同model经过gradient descent找到的best function f ∗ f^* f∗ 。 ↩︎
举例:对于model 5, y = b + w 1 ∙ x c p + w 2 ∙ ( x c p ) 2 + w 3 ∙ ( x c p ) 3 + w 4 ∙ ( x c p ) 4 + w 5 ∙ ( x c p ) 5 y=b+w_1 \bullet x_{cp}+w_2 \bullet (x_{cp})^2+w_3 \bullet (x_{cp})^3 + w_4 \bullet (x_{cp})^4 + w_5 \bullet (x_{cp})^5 y=b+w1∙xcp+w2∙(xcp)2+w3∙(xcp)3+w4∙(xcp)4+w5∙(xcp)5,来说,令变量 w 5 = 0 w_5=0 w5=0,可以得到model 4, y = b + w 1 ∙ x c p + w 2 ∙ ( x c p ) 2 + w 3 ∙ ( x c p ) 3 + w 4 ∙ ( x c p ) 4 y=b+w_1 \bullet x_{cp}+w_2 \bullet (x_{cp})^2+w_3 \bullet (x_{cp})^3 + w_4 \bullet (x_{cp})^4 y=b+w1∙xcp+w2∙(xcp)2+w3∙(xcp)3+w4∙(xcp)4。其它同理可得。 ↩︎
δ ( x s = P i d g e y ) = { 1 , I f ( x s = P i d g e y ) 0 , o t h e r w i s e \delta (x_s=Pidgey) = \left \{ \begin{aligned} 1,& If(x_s=Pidgey) \\ 0,&otherwise \end{aligned} \right. δ(xs=Pidgey)={1,0,If(xs=Pidgey)otherwise ↩︎
假设我们的model是 y = b + ∑ w i ∙ x i y=b+\sum w_i \bullet x_i y=b+∑wi∙xi,若输入的其中一项 x t x_t xt变化到了 x t + Δ x x_t + \Delta x xt+Δx,原先的输出将从 y y y变成 y + w t ∙ Δ x y+ w_t\bullet \Delta x y+wt∙Δx。若 w t w_t wt越小,则这个输出的变化就越小,即函数 f ∗ f^* f∗越平滑。
为什么不考虑参数 b b b?Regularization是去调整一个function的平滑程度,而参数 b b b是不影响函数的平滑程度的。 ↩︎为什么要使 f ∗ f^* f∗更平滑?在测试时,如果有一些输入被干扰了,一个比较平滑的函数会受到比较小的影响。 ↩︎
这是非常正常的,因为上文提到, λ \lambda λ 越大,考虑Training Error这一项越少。这也是不必担心的,相比于在Training Data上的Average Error,我们更关心函数在Testing Data上的Average Data。 ↩︎














![[JAVA实现]微信公众号网页授权登录,java开发面试笔试题](https://images.cnblogs.com/OutliningIndicators/ExpandedBlockStart.gif)