Regularization(正则化)

前言

这一章还是紧接着上一章的，在上一章我们讨论了logistic regrsssion(逻辑回归)，在更早我们还讨论了linear regression(线性回归)，对于这两种问题，我们在进行用函数去预测结果时，我们根据已知的数据集去推测一个函数关系，然后去模拟输入和输出的关系。那么问题就来了，什么样的函数关系更能准确表示两者之间的关系呢？对于linear regression问题，是不是找到一个函数关系能表示训练集的所有数据之间输入和输出之间的关系就是最好了？而对于logistic regression问题，是不是找到一个边界决策可以完全把所有数据进行完全地无误分离出来就最好了？答案先卖个关子，在这一章我们将和大家讨论这个问题。

最后，如果在内容见解上有什么不对地地方，希望大家不吝赐教，谢谢！

【机器学习系列】【第四章：逻辑回归】【第六章：神经网络】

第五章 Regularization(正则化)

5.1 The problem of overfitting(过度拟合问题)

5.1.1 linear regression

对于linear regression问题，我们还是用前面的房子的price和size来说明这个问题，对于我们给定的一些price和size的数据集，我们可以用如图1的一些函数关系去模拟两者之间的关系。

图1 用不同的函数关系去描述price和size的关系

在图1中，我们可以看到，对于第一个，我们用一次函数 $\theta _{0}+\theta _{1}x$ 去描述两者之间的关系，对于有很多数据不能更好地落在这条线上，而且我们清楚在实际中，随着后面size越大，price是趋于稳定的，而对于这个关系来说是无限上升的，明显不符合两者之间的关系，对于这个问题我们称为underfit(不充分拟合)，再看第二个，我们用一个二次函数 $\theta _{0}+\theta _{1}x+\theta _{2}x^2$ 来描述两者之间的关系，对于训练中的数据少数落在这个函数以外，对于函数的趋势走向也比较符合二者之间的关系，所以对于这个函数来说，就是比较符合训练集的，我们称为just right，最后来看看第三个，我们用了一个四次函数 $\theta _{0}+\theta _{1}x+\theta _{2}x^2+\theta _{3}x^3+\theta _{4}x^4$ 来描述两者之间的关系，虽然使训练集中的数据都落在在了函数上，但由于曲线太过于扭曲，不符合整体的走向，所以这也不是很合理的函数关系，我们把这个问题就称为overfit。

在上述这个问题中，我们很直观地了解了什么是overfit，而对于overfit来讲，如果我们有更多的特征，则h(x)更接近y，这个时候我们的误差函数 $J(\theta )=\frac{1}{2m}\sum_{i=1}^{m}(h(x^{(i)})-y^{(i)})^2\approx 0$ ，对于J( $\theta$ )来看似乎是很好的关系，但对于预测新的数据来看，是不能很好地预测出比较合理的结果的。

5.1.2 Logistic regression

现在给大家介绍下logistic regression关于overfit的问题，下面还是用一个具体的例子来向大家说明这个问题，如图2所示。

图2 用不同的边界决策去分离两类

如图2所示，对于具体的分析，我就不跟大家一一道来了，和linear regression问题一样，对于第一个仍然是underfit，第二个是just right，第三个就是overfit。

5.2 解决过度拟合的问题

根据以上的分析，我们该如何来解决过度拟合了？当特征变量很多时，我们用来分析出的h(x)会更接近y，出现过度拟合的可能性更大，所以第一个解决办法就是减少特征变量，先通过手动选择减少特征变量，再进行模型选择。但很多时候，有很多变量是不能之间去掉的，比如房子price的问题中，不管是size，age of house，no. of bedrooms等等都是不可少的特征，那么我们就有了第二中解决办法，即我们要给大家详细介绍的regularization(正则化)，保持所有的特征，来减少 $\theta _{j}$ ，在后面会跟大家详细介绍。

5.3 Cost Function(代价函数)

在这里，我们又来讨论这个cost function，在这里还是用前面的linear regression中的房子price和size的问题来向大家说明这个问题。如图3所示。

图3 Just right和overfit

在图3中，我们对两者进行比较，会发现对于overfit这个表达式来看，如果没有了 $\theta _{3}x^3+\theta _{4}x^4$ 后面这两项，或者让他们的影响不是很大，则可以变成前面的关系，前面我们也说了，我们可以让 $\theta _{3},\theta _{4}$ 的值很小，则后面两项就没什么影响了。在这里我们可以对cost function重新定义为： $\frac{1}{2m}\sum_{i=1}^{m}(h(x^{(i)})-y^{(i)})^2+1000\theta _{3}+1000\theta _{4}$ ，关于 $\theta _{3},\theta _{4}$ 前面的系数1000，只是我们随便设置的一个数，足够大就行，对于这个新的表达式，在前面的章节中，我们也说了代价函数是用来评判我们所选的模型是否符合数据集的关系，所以我们需要代价函数的值尽量小，为0最好，而对于这个新的式子，对于后面新添的两项，如果我们希望整个式子的值比较小，则 $\theta _{3},\theta _{4}$ 的值必须很小才行，这样即达到了我们前面的要求。

对于这个regularization(正则化)问题，就是我们使我们的参数 $\theta _{1},\theta _{2},...,\theta _{n}$ 减小，这样就可以减小过度拟合。对于特征还是 $x_{1},x_{2},...,x_{n}$ ，参数还是： $\theta _{0},\theta _{1},\theta _{2},...,\theta _{n}$ ，而 $J(\theta )=\frac{1}{2m}[\sum_{i=1}^{m}(h(x^{(i)})-y^{(i)})^2+\lambda \sum_{j=1}^{n}\theta _{j}^{2}]$ ，注意后面新添的一项，我们对于 $\theta _{0}$ 是不做惩罚的。对于后面新添的一项，我们则称为正则化变量。

对于 $\lambda$ 我们只知道要选取一个比较大的数，那么 $\lambda$ 选取太大会怎么样了？对于这个问题，我们还是用一个房子的例子来向大家说明这个问题。如图4所示，对于我们这个新的代价函数 $J(\theta )=\frac{1}{2m}[\sum_{i=1}^{m}(h(x^{(i)})-y^{(i)})^2+\lambda \sum_{j=1}^{n}\theta _{j}^{2}]$ ，如果我们所选 $\lambda$ 太大，即意味着 $\theta _{1},\theta _{2},\theta _{3},\theta _{4}$ 会很小，接近于0，在这里我们就几乎可以不考虑后面的四项了，那么这个模型函数就成了h(x)= $\theta _{0}$ ，是一条水平的直线，很明显这个没有很好地描述这个关系，即失败的预测。

图4 price and size

5.4 Regularized linear regression(线性回归的正则化)

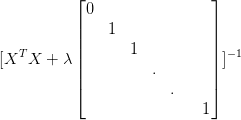
对于 $J(\theta )=\frac{1}{2m}[\sum_{i=1}^{m}(h(x^{(i)})-y^{(i)})^2+\lambda \sum_{j=1}^{n}\theta _{j}^{2}]$ ，我们在前面也进行了分析，而我们还需要讨论的一个问题就是 $\theta _{j}$ 的问题，我们做的那么多工作，就是为了选择出最好的 $\theta _{j}$ ，那么对于这个新的代价函数，我们的 $\theta _{j}$ 会是怎样了？关于 $\theta _{j}$ ，这个式子是永远不会变的，就是 $\theta _{j}:=\theta _{j}-\frac{\partial }{\partial \theta _{j}}J(\theta )$ ，所以 $\theta _{0}:=\theta _{0}-\alpha \frac{1}{m}\sum_{i=1}^{m}(h(x^{(i)})-y^{(i)})x_{0}^{(i)}$ ， $\theta _{j}:=\theta _{j}-\alpha [\frac{1}{m}\sum_{i=1}^{m}(h(x^{(i)})-y^{(i)})x_{j}^{(i)}+\frac{\lambda }{m}\theta _{j}]$ ，对这个式子进行整理下，得到 $\theta _{j}:=\theta _{j}(1-\alpha \frac{\lambda }{m})-\alpha \frac{1}{m}\sum_{i=1}^{m}(h(x^{(i)})-y^{(i)})x_{j}^{(i)}$ ，关于 $1-\alpha \frac{\lambda }{m}$ 是小于1的，所以有了 $\lambda$ 使 $\theta _{j}$ 变小了。

5.5 Regularized logistic regression(逻辑回归的正则化)

对于logistic regression问题，在前面我们也给出了如图5所示的overfit问题。同样的，我们对cost function做出了一些改变， $J(\theta )=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}logh(x^{(i)})+(1-y^{(i)})log(1-h(x^{(i)}))]+\frac{\lambda }{2m}\sum_{j=1}^{n}\theta _{j}^{2}$ ，而对于 $\theta _{j}$ 的求法也做出对应的改变， $\theta _{0}:=\theta _{0}-\alpha \frac{1}{m}\sum_{i=1}^{m}(h(x^{(i)})-y^{(i)})x_{0}^{(i)}$ ， $\theta _{j}:=\theta _{j}-\alpha [\frac{1}{m}\sum_{i=1}^{m}(h(x^{(i)})-y^{(i)})x_{j}^{(i)}+\frac{\lambda }{m}\theta _{j}]$ ，注意这里的h(x)= $\frac{1}{1+e^{-\theta ^{\top }x}}$ 。