CSDN话题挑战赛第2期
参赛话题：学习笔记

学习之路，长路漫漫，写学习笔记的过程就是把知识讲给自己听的过程。这个过程中，我们去记录思考的过程，便于日后复习，梳理自己的思路。学习之乐，独乐乐，不如众乐乐，把知识讲给更多的人听，何乐而不为呢?

• 项目中解决的问题

安装Node环境，这是目前前端技术的基础环境，大部分技术栈都依赖它，所以必须要安装。
➢ 包管理工具NPM是伴随Node安装的，Node安装之后，NPM也自动安装完成了。建议使用淘宝镜像CNPM，在后面会讲到如何切换到淘宝镜像使用。
➢ Vue-cli的安装以及初始化vue项目。
➢ 与Vue框架搭配使用的UI框架选择iView框架，UI框架可以大大节约开发时间和成本，如何安装配置后面会讲到。
➢ 页面路由选择使用vue-router插件来完成。
➢ Vue项目里面的数据共享，选择使用VueX来管理。
➢ 选择使用ECMAScript 6语法编写JavaScript。
➢ 选择Vue官方推荐的 axios插件发送异步请求。

• 工具准备

Node.js 是一个基于Chrome V8引擎的JavaScript运行环境。Node.js使用了一个事件驱动、非阻塞式I/O的模型，既轻量又高效。另外，Node.js可以理解为JavaScript运行时环境（runtime），runtime 类似于国际会议中的同声翻译。接下来看一下如何安装Node.js。
从官网下载Node.js，官方提供适用不同系统、不同系统位数的安装包，读者可以根据自己的计算机配置进行选择性下载。
在Windows系统中，按Win+R组合键调出“运行”窗口，输入“cmd”打开命令提示符窗口。输入“node -v”可得到对应的Node.js版本，说明Node.js已经安装成功。
Node.js的包管理器NPM是全球最大的开源库生态系统，它集成在Node.js中，在安装Node.js的时候就已经自带了NPM包管理工具。验证NPM是否安装成功的方法同验证Node.js的方法。
在命令行窗口中输入“npm -v”可得到NPM的版本，说明NPM已经安装成功。
NPM安装成功之后，接下来要使用NPM安装依赖包了。那么如何安装依赖包呢？首先打开命令提示符窗口，了解一下NPM常用命令。
npm install-g　　　//安装模块　加不加“-g”代表是不是全局安装
npm list　　　　　//查看某个模块的版本号
npm uninstall　　　//卸载模块
npm update　　　　//更新模块
安装cnpm
来自淘宝NPM镜像官网：
这是一个完整的 npmjs.org 镜像，可以用此代替官方版本（只读），同步频率目前为10分钟一次，以保证尽量与官方服务同步。
既然淘宝NPM镜像这样方便，那么该如何使用呢？
使用方法比较简单，只需要在命令行中输入以下内容，按回车键等待安装成功即可。
npm install -g cnpm --registry=https://registry.npm.taobao.org
安装CNPM成功之后，输入“cnpm -v”，如图1.11所示，可以查看到当前CNPM版本，所有用到NPM的地方便可以全部替换为CNPM，这样就成功切换到淘宝NPM镜像上了。

• Vue-cli脚手架

Vue-cli是一个官方命令行工具，可用于快速搭建大型单页面应用。该工具提供开箱即用的构建工具配置，带来现代化的前端开发流程，只需几分钟即可创建并启动一个带热重载、保存时静态检查，以及可用于生产环境构建配置的项目。
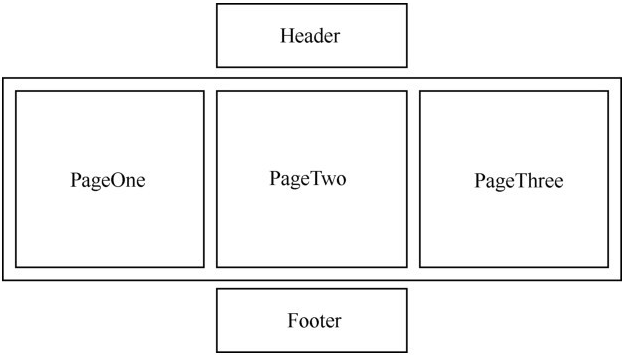
单页面应用（Single Page Web Application，SPA）
只有一个Web页面的应用，如图1.12所示，是一种从Web服务器加载的富客户端，单页面跳转仅刷新局部资源，公共资源（js、css等）仅需加载一次。
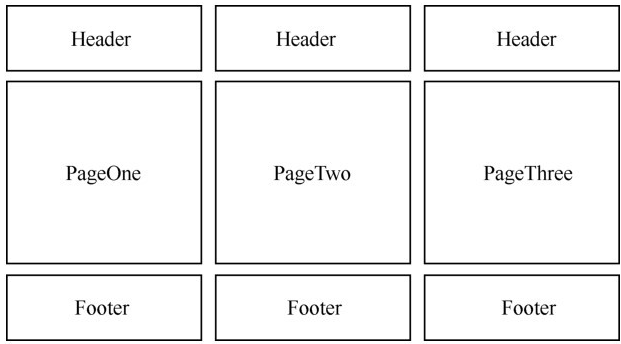
多页面应用（Multi-Page Application，MPA）
多页面跳转刷新所有资源，每个公共资源（js、css 等）需选择性重新加载

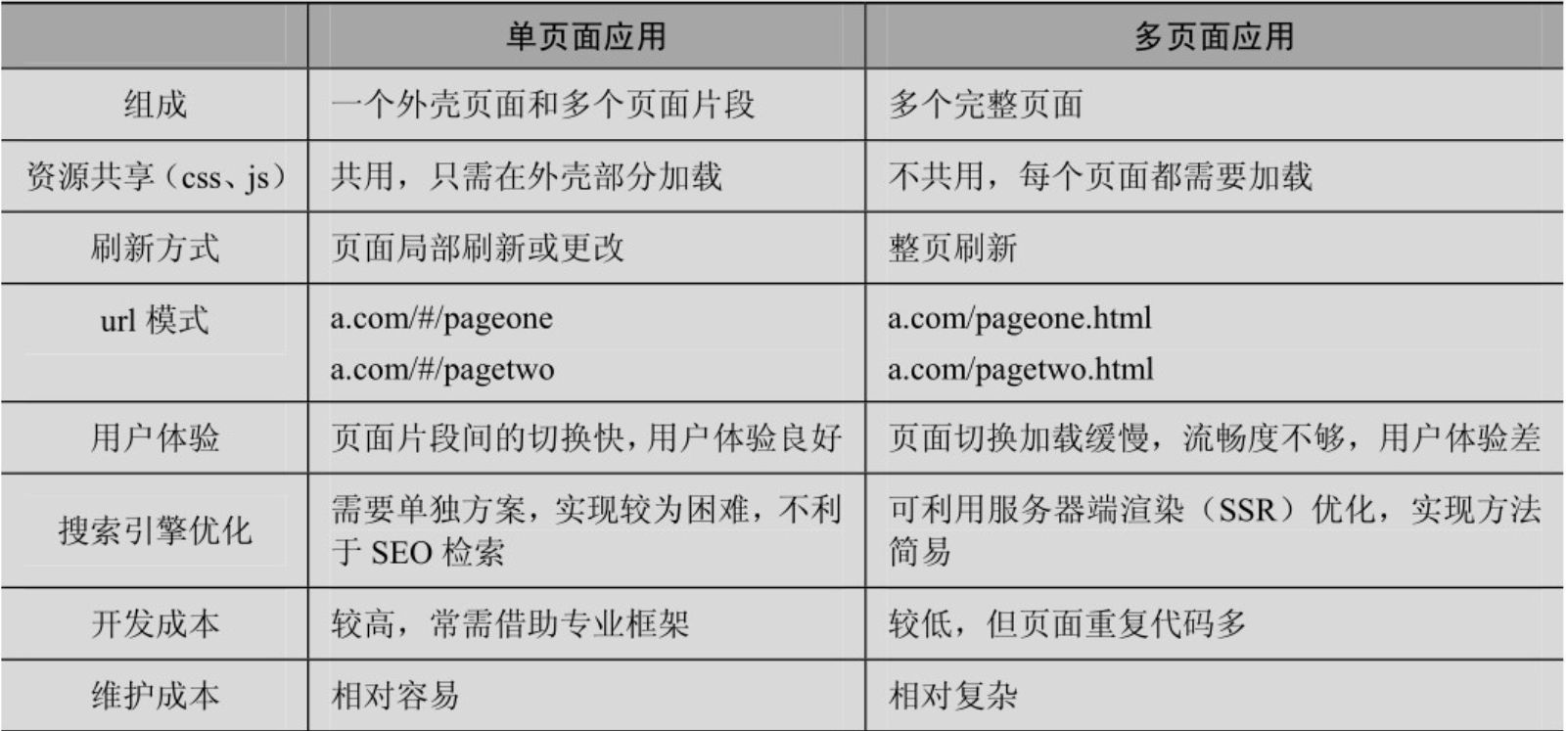
单页面和多页面应用详细对比分析

Vue-cli是用Node编写的命令行工具，需要进行全局安装。首先打开命令提示符窗口，输入如下命令进行安装：
cnpm install vue-cli -g
安装Vue-cli脚手架之后，执行“vue -v”如果能显示Vue-cli的版本号，表示安装成功。在以后安装依赖包之后，可以通过 --version或者简写 -v来查看对应的版本号，如果能显示对应版本号，则说明安装成功。
另外还需要全局安装Webpack，关于Webpack的内容后面会介绍到，这里只需先安装：
cnpm install webpack -g
到这里，准备工作已经结束了，可以使用Vue-cli脚手架快速搭建单页面应用，只需在命令行窗口输入以下命令：
vue init webpack <项目名称>
例如：vue init webpack dm。
执行创建项目命令之后，会有一些命令行交互，在这里可以初始化一些项目信息

• 效果

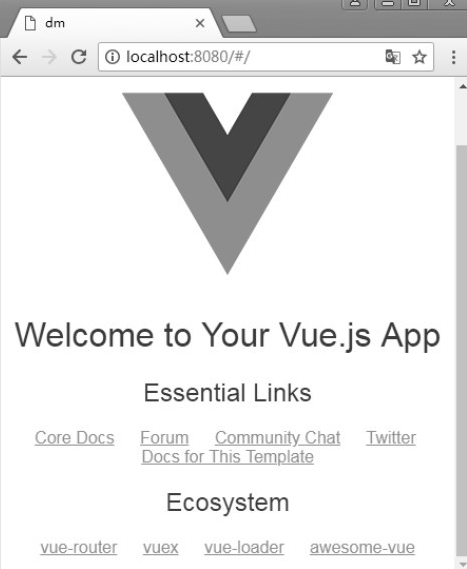
最后启动项目，运行命令：npm run dev。
启动项目之后需要打开浏览器，输入http://localhost:8080，确认项目是否运行成功，项目启动成功之后，

项目启动成功之后，看一下项目目录结构，主要的目录结构如下：
➢ src文件夹放置组件和入口文件。
➢ static文件夹放置静态资源文件。
➢ index.html为文件入口。

…

提醒：在发布作品前请把不用的内容删掉