在学习STM32的时候,我发现了一个很值得研究学习的问题,下面,用我的理解来阐述一遍,这其中的原理。
首先请看电路图
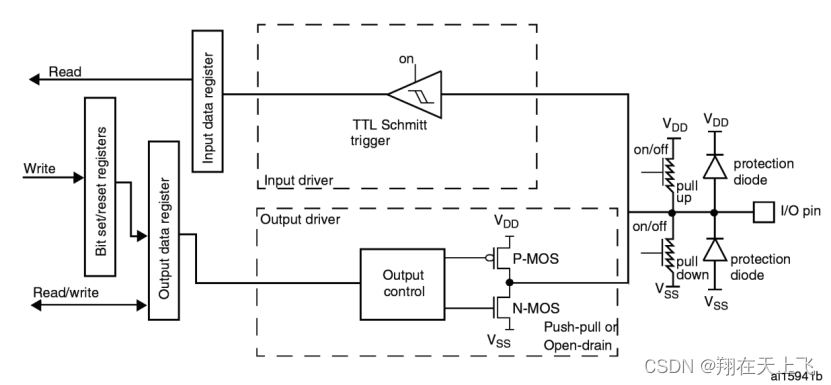
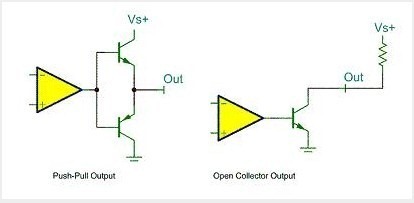
在给GPIO配置输出的时候,其有两种工作模式可选,分别是推挽输出和开漏输出。
在此之前先得了解mos管的工作原理,为了方便大家理解,我用通俗的语言来阐述

这是一个PMOS,他可以理解成一个低电平(逻辑0)开启的开关,图中的小圆点是非门的意思,也就给我们提示需要用一个低电平来导通这个pmos管
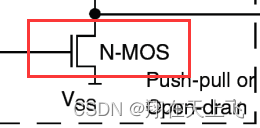
这是一个NMOS,他可以理解成一个高电平(逻辑1)开启的开关
在有了上面的认知,我们再来理解下面的问题
1、推挽输出
推挽输出的时候,是不需要上拉电阻的,其本身就有足够的驱动能力,但是其缺点是无法进行“线与”,一但进行了高低电平的“线与”, 就会发生短路的现象。
1.1分析其输出(用逻辑0和1来分析)
| 输入 | PMOS | NMOS | 输出 |
| 0 | 导通 | 不导通 | 1 |
| 1 | 不导通 | 导通 | 0 |
推挽输出时,不管是输入0,还是1,都会有一个mos管是工作在导通状态。
当输入0时,PMOS导通,那就把上面想成一个导线,NMOS不导通,那就想成电阻无穷大,根据节点电压,或者说分压原理,输出的那一段电压值,其实就是分在下面NMOS两端的电压,由于其阻止很大,因此分的也大,几乎是全部,也就是逻辑1了,
输入1时的情况也可以用我上面说的那种方法来理解,此处就不过多赘述了
1.2分析其不可“线与”

这就是所谓的“线与”,就是把前一个的输出,直接接到后一个作为后一个的输入。而我上面画出的这种情况,也就是在最开始的时候输入一个0,其线与后就会反生如上图所示的短路(图中的叉叉表示不导通),所以我们说推挽输出,不可以“线与”。
2、开漏输出
所谓的开漏就是,没有VDD,也就是如下图所示的状态

由于上面不接VDD了,上面的PMOS也就不工作了,真正工作的只有下面的NMOS,原来的电路也就可以等效成下面这样,其与单个NMOS工作没什么差别。

| 输入 | NMOS状态 | 输出 |
| 0 | 不导通 | 高阻态 |
| 1 | 导通 | 0 |
在其不导通的时候,nmos管相当于一个很大的电阻,也就是我们所说的高阻态;而在其导通的时候,就相当于直接接地了,所以就是逻辑0。
由于其不导通和导通的时候是高阻和0,所以其可以进行“线与”,就相当于多个电阻进行连接,并没有什么电源,也就不存在什么短路。
因此,为了提高其驱动能力,STM32的线路设计上在后面又给它加了个上拉电阻,也就是下面这个图,这也是为什么开漏输出需要上拉电阻的原因。
另外,使用开漏输出,还可以根据上拉电阻的阻值大小不同,控制输出电平的大小,其中原理就是一个很简单的分压原理, 也就是说其可以进行电压转换。
总结
推挽输出:不需要上拉电阻,不可“线与”,不可电平转换
开漏输出:需要上拉电阻,可以进行“线与”,可以电平转换