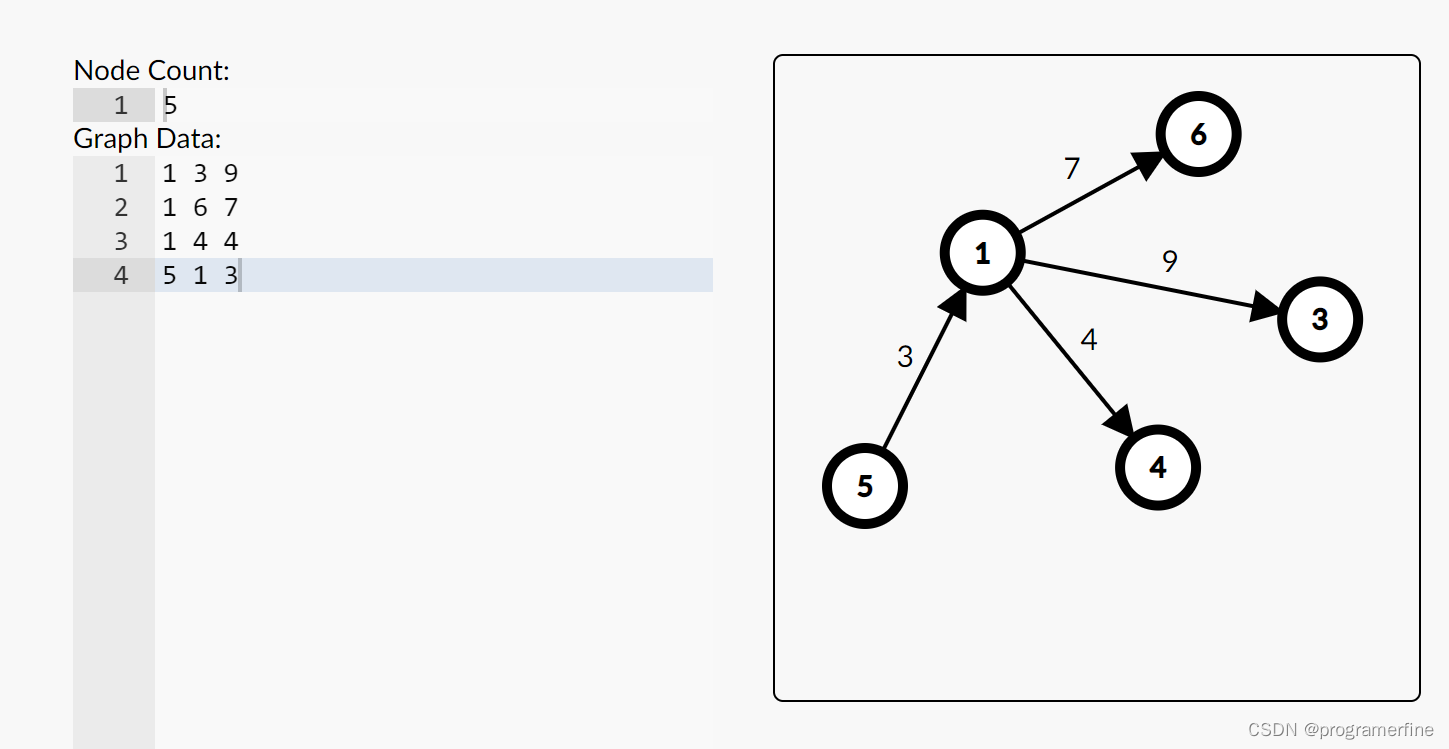
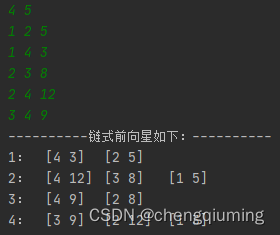
存储一个图通常有两种方式:邻接矩阵和邻接表。如果一个图中的边非常少,那么邻接矩阵就比较稀疏,浪费空间,如果点非常多,则矩阵的内存有可能会爆掉。用向量实现的邻接表在点非常多的时候同样比较慢,在一些题目中会超时。链式前向星是在邻接表基础上的一种优化,其优秀的时空复杂度可以帮助我们在一些边和点都比较多情况下加快对图的遍历。例如DFS、BFS等。我们可以结合DFS的过程来理解链式前向星。
DFS:
DFS算法的实现过程可以这样理解:
- 以当前点作为起点,在所有与该起点连接着的边中随便找一条,然后跳到这条边的终点上。
- 再将当前跳到的点当做起点,重复1。
- 若跳到某一点后,没有以这个点为起点的边了,就原路返回到之前的起点上,找一条与这条不同的边,再跳到它的终点上。
也就是说,DFS对两件事感兴趣:一是边的终点是什么,二是一个点连接了多少条不同的边。
链式前向星:
链式前向星的结构中正好包括了这两点,链式前向星的结构定义如下:
struct node
{int to;int next;
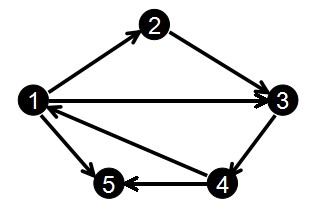
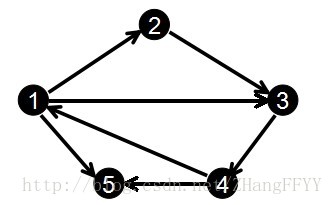
}edge[maxn];链式前向星以边为单位进行储存。其中,成员to表示这条边的终点,而next就比较重要了,表示跟本条边的起点相同的前一条边,在edge数组中的下标,如果这条边的起点是第一次出现的,则置为0。也就是说,链式前向星的next属性,像链表一样,将图中起点相同的边连在了一起。例如下面这个图:
我们输入边的顺序为:
1 2
2 3
3 4
4 5
1 3
1 5
4 1
那么我们得到的edge数组为:
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 起点 | 1 | 2 | 3 | 4 | 1 | 1 | 4 |
| to | 2 | 3 | 4 | 5 | 3 | 5 | 1 |
| next | 0 | 0 | 0 | 0 | 1 | 5 | 4 |
当我们想要得到一条边的终点时,就调用edge[i].to,当我们想得到这个起点连接的其他边时,就可以调用edge[i].next。那么现在的问题就是如何快速求next属性。
解决方法就是再定义一个数组head,head[i]表示最近一次输入的以i为起点的边在edge数组中的下标。
用链式前向星建图的整个过程并不复杂,下面来看建图的函数:
struct node
{int to;int next;
}edge[maxn];
int head[maxn];
int cnt=1;//表示edge数组的下标,也可以表示已经存入的边数
void add(int from,int t)
{edge[cnt].to=t;edge[cnt].next=head[from];head[from]=cnt++;
}链式前向星遍历图的核心代码是:
for(int i=head[x];i!=0;i=edge[i].next)在对某一点所连接的所有边的遍历过程中,调用edge[i].next,就像链表一样,将所有起点相同的边都串在了一起。而且,最先输入的边会最晚遍历到,这是由next的属性所造成的。
链式前向星+DFS:
#include<iostream>
using namespace std;
const int maxn=1000;
struct node
{int to;int next;
}edge[maxn];
int head[maxn];
int cnt=1;
void add(int from,int t)
{edge[cnt].to=t;edge[cnt].next=head[from];head[from]=cnt++;
}
bool s[maxn];
void dfs(int x)
{s[x]=true;printf("%d ",x);for(int i=head[x];i!=0;i=edge[i].next){if(!s[edge[i].to])dfs(edge[i].to);}
}int main()
{int u,v,w;int n;cin>>n;while(n--){cin>>u>>v;add(u,v);}dfs(1);return 0;
}链式前向星+BFS:
用队列实现BFS,中间用链式前向星存储图结构。
#include<iostream>
#include<queue>
#include<cstdio>
using namespace std;
const int maxn=500005;
//保存图结构
struct node
{int to;int next;
}e[2*maxn];
int head[maxn];
int cnt;
void add(int a,int b)
{e[++cnt].to=b;e[cnt].next=head[a];head[a]=cnt;
}
bool vis[maxn];
int main()
{int n,u,v;cin>>n;while(n--){cin>>u>>v;add(u,v);}queue<int> q;q.push(1);while(!q.empty()){int temp=q.front();q.pop();vis[temp]=true;printf("%d ",temp);for(int i=head[temp];i;i=e[i].next){if(!vis[e[i].to])q.push(e[i].to);}}return 0;
}