图的存储 —— 链式前向星

article/2025/10/16 11:56:42

链式前向星采用了一种静态链表存储方式，将边集数组和邻接表相结合，可以快速访问一个节点的所有邻接点，在算法竞赛中被广泛应用。

链式前向星有如下两种存储结构。

struct node{int to , next , w;
}edge[maxe]; //边集数组，对边数一般要设置比maxn x maxn 大的数，题目有要求除外
int head[maxn]; //头节点数组

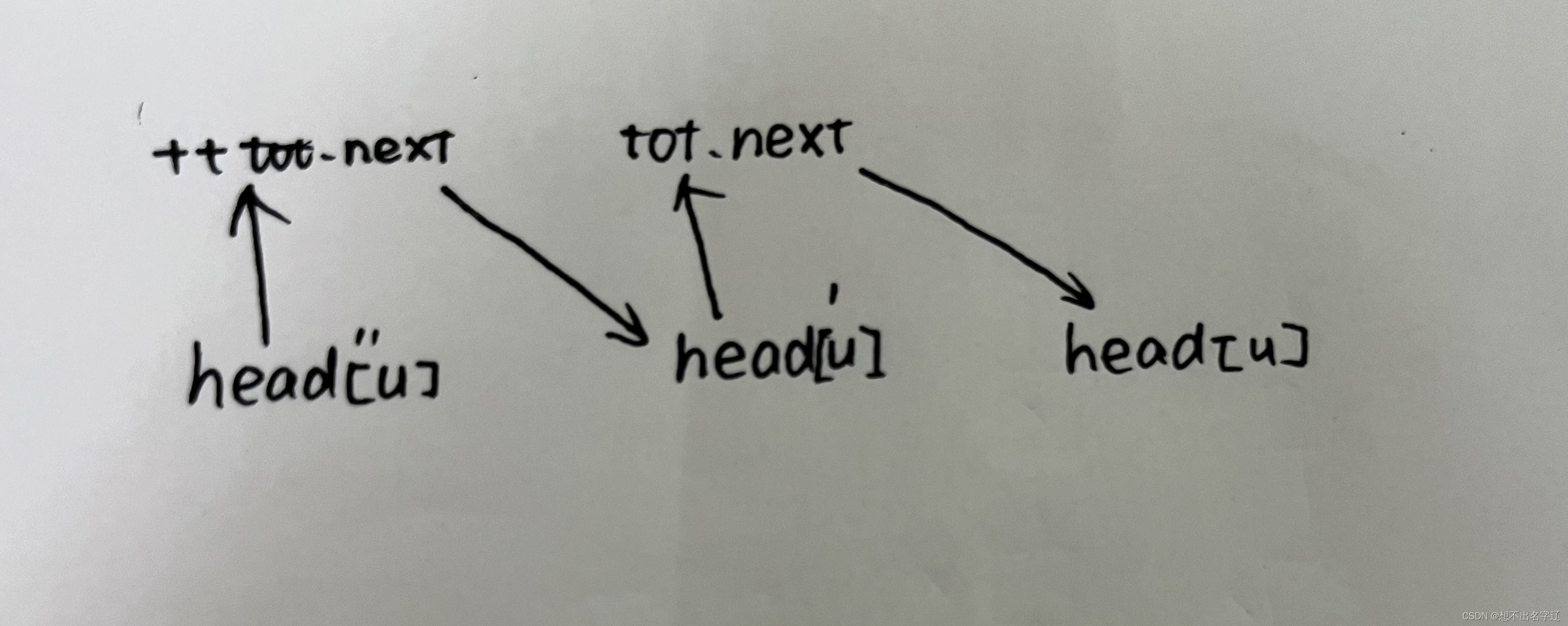
每一条边的结构都如下图所示。

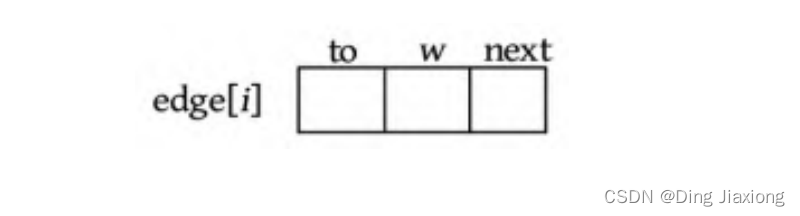
在这里插入图片描述

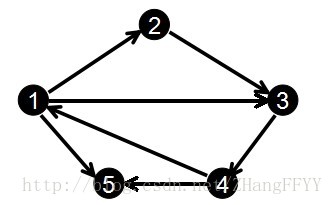
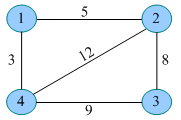
例如，一个无向图如下图所示：

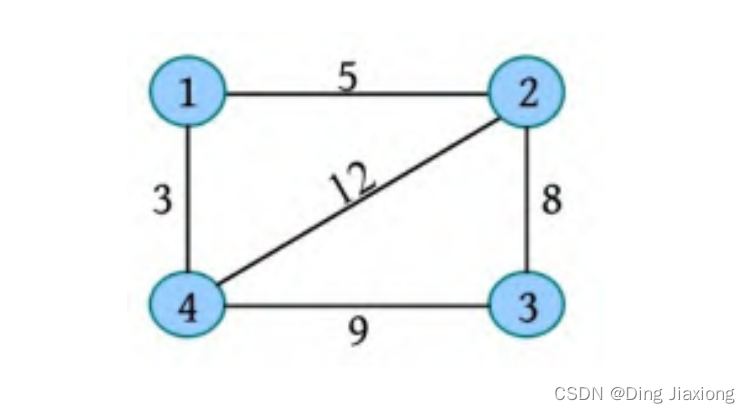
在这里插入图片描述

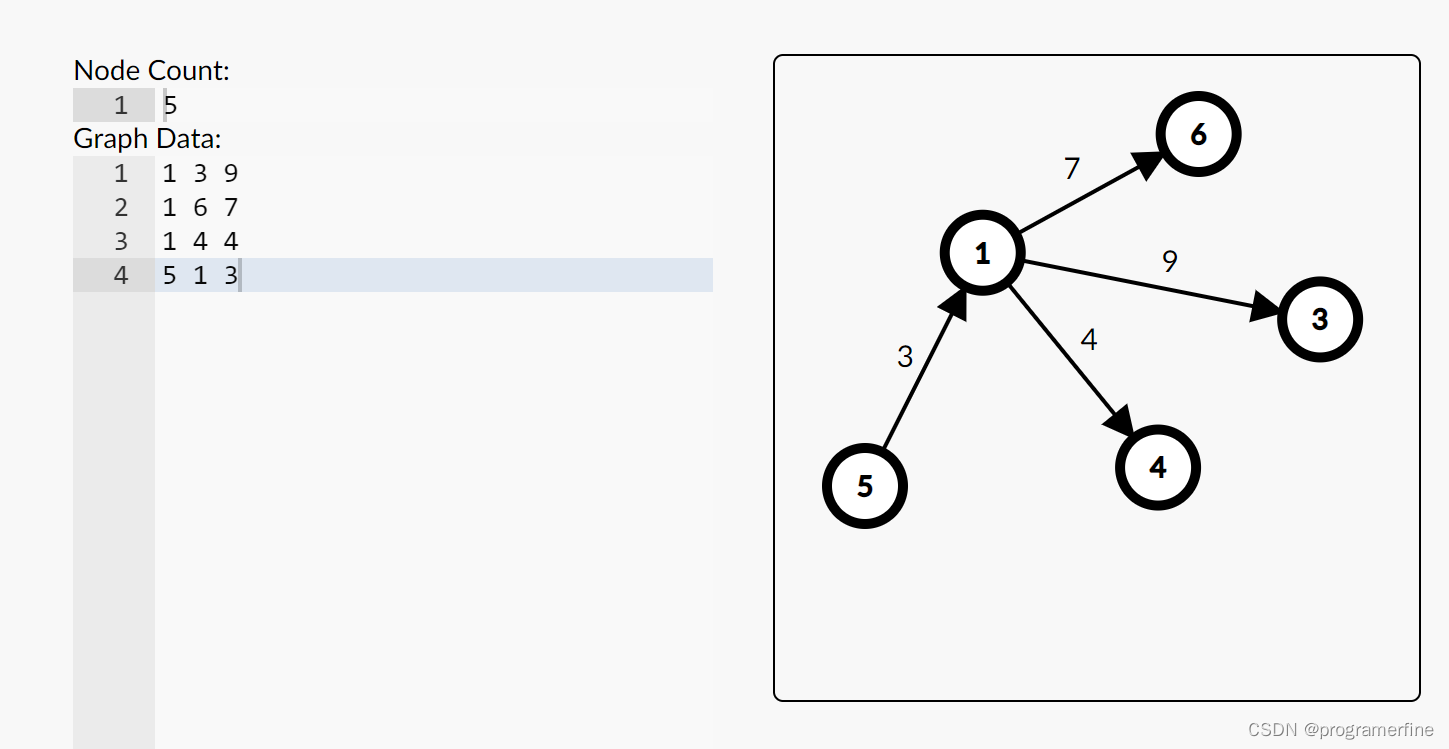
按以下顺序输入每条边的两个端点，建立链式前向星，过程如下。

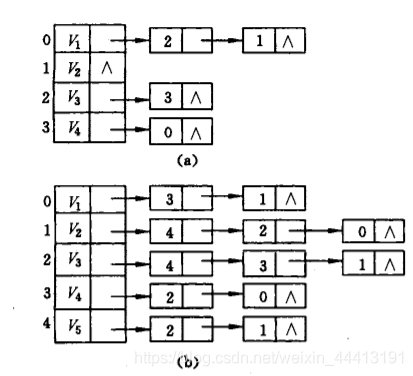
① 输入1 2 5。创建一条边1-2，权值为5，创建第1条边edge[0]，将该边链接到节点1的头节点中（初始时head[]数组全部被初始化为-1）。edge[0].next=head[1]; head[1]=0，表示节点1关联的第1条边为0号边，如下图所示。

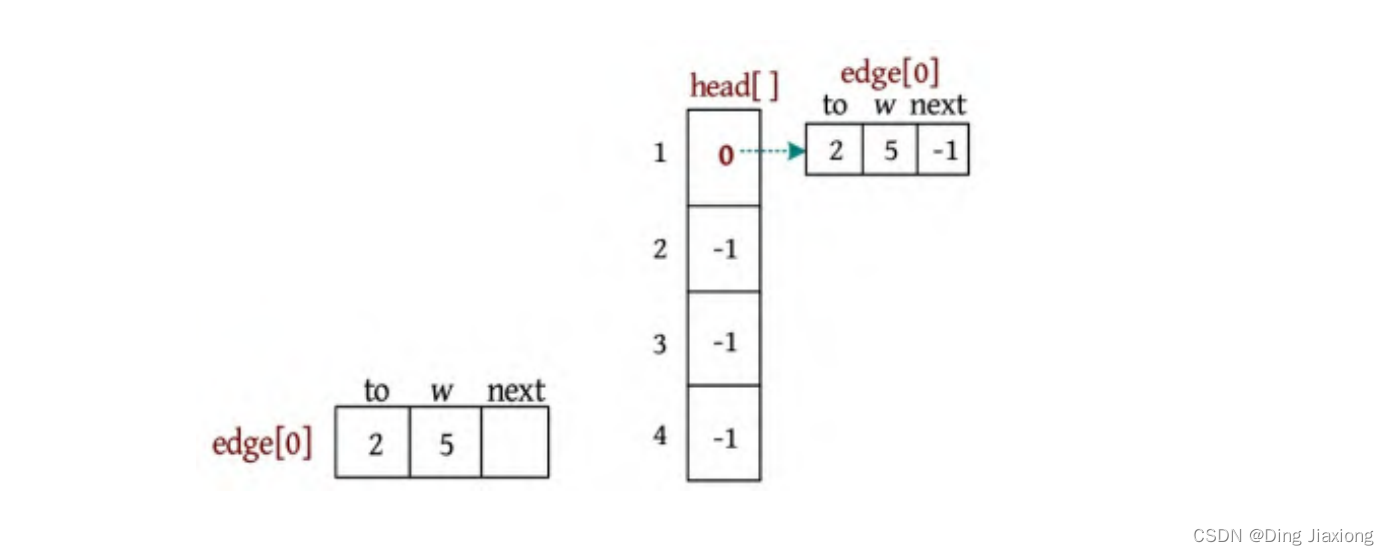
在这里插入图片描述

图中的虚线箭头仅表示它们之间的链接关系，不是指针。

因为是无向图，所以还需添加它的反向边2-1，权值为5。创建第2条边edge[1]，将该边链接到节点2的头节点中。即edge[1].next=head[2]; head[2]=1；表示节点2关联的第1条边为1号边，如下图所示。

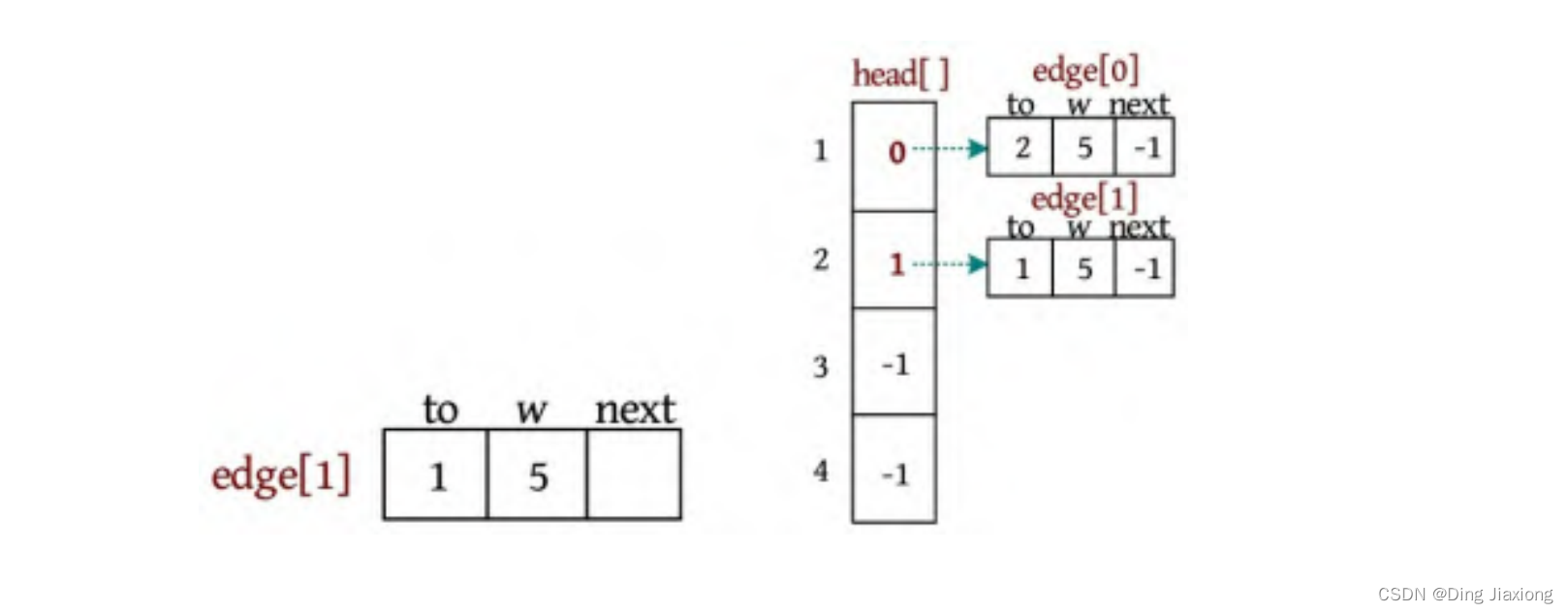
在这里插入图片描述

② 输入1 4 3。创建一条边1-4，权值为3。创建第3条边edge[2]，将该边链接到节点1的头节点中（头插法）。即edge[2].next=head[1]; head[1]=2，表示节点1关联的第1条边为2号边，如下图所示。

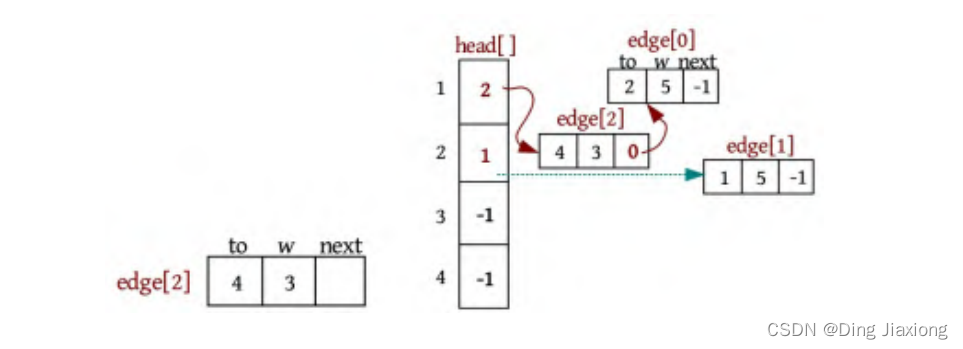
在这里插入图片描述

因为是无向图，所以还需要添加它的反向边4-1，权值为3。创建第4条边edge[3]，将该边链接到节点4的头节点中。即edge[3].next=head[4]; head[4]=3，表示节点4关联的第1条边为3号边，如下图所示。

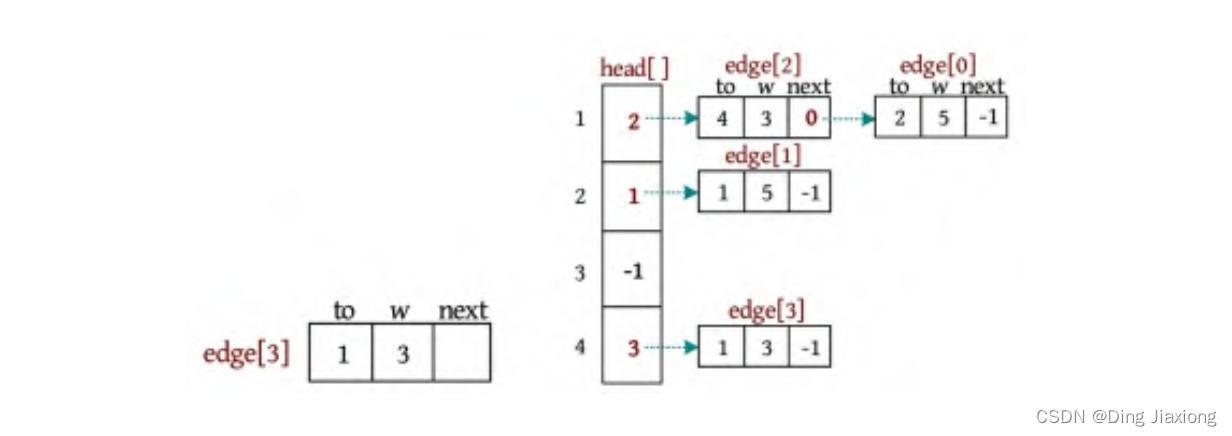
在这里插入图片描述

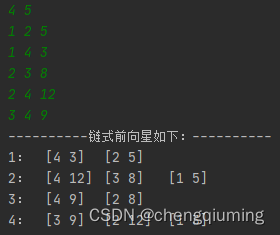
③ 依次输入三条边2 3 8、2 4 12、3 4 9，创建的链式前向星如下图所示。

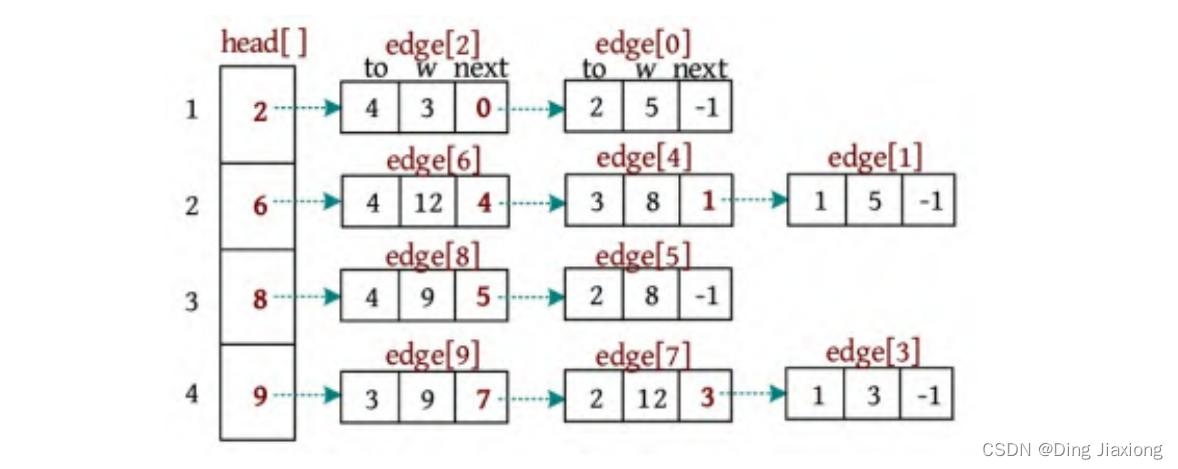
在这里插入图片描述

添加一条边u v w 的代码如下：

void add(int u, int v, int w){ //添加一条边edge[cnt].to = v;edge[cnt].w = w;edge[cnt].next = head[u];head[u] = cnt ++;
}

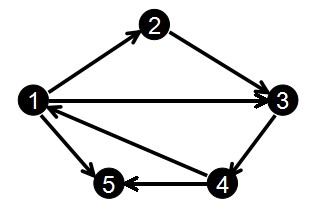
如果是有向图，则每输入一条边，都执行一次add(u ,v ,w )即可；如果是无向图，则需要添加两条边add(u ,v ,w ); add(v ,u ,w)

使用链式前向星访问一个节点u 的所有邻接点：

for(int i = head[u] ; i != -1 ; i = edge[i].next){ //i != -1 可以写为~iint v = edge[i].to;  //u的邻接点int w = edge[i].w; //u - v 的权值...
}

链式前向星的特性：

和邻接表一样，因为采用头插法进行链接，所以边的输入顺序不同，创建的链式前向星也不同。
对于无向图，每输入一条边，都需要添加两条边，互为反向边。例如，输入第1条边1 2 5，实际上添加了两条边，如下图所示。这两条边互为反向边，可以通过与1的异或运算得到其反向边，0^1=1，11=0。也就是说，如果一条边的下标为i ，则其反向边为i ^1。这个特性在网络流中应用起来非常方便。

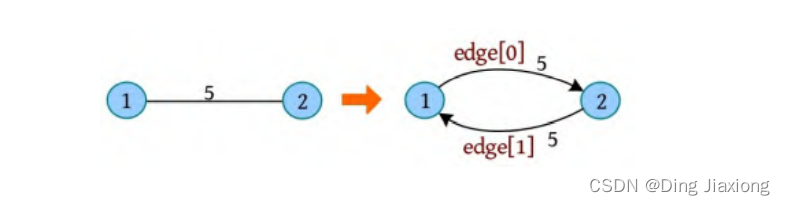
在这里插入图片描述