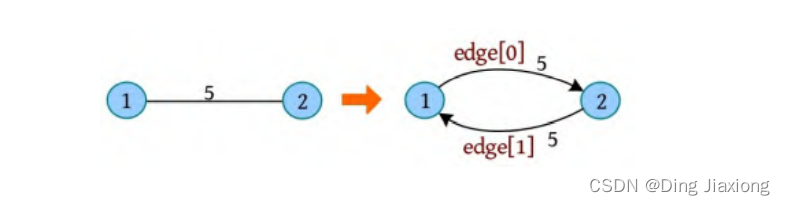
文章目录
- 链式前向星
- 完整代码
链式前向星
链式前向星是一种图的存储方式,相比于 邻接矩阵和邻接表 ,链式前向星是一种静态链表存储,用边集数组和邻接表相结合,可以快速访问一个顶点的所有邻接点。
在某些算法题中使用还很频繁,我就是因为看不懂别人发的题解,所以就学习了这种存储图的方式。
不多啰嗦,也许你看别人发的题解中都有这样一段代码:
void add_edge(int u, int v, int w)
{edge[cnt].to = v;edge[cnt].w = w;edge[cnt].next = head[u];head[u] = cnt++;
}
你是否在一开始有和我一样的疑惑,这是个什么东西???
这就是链式前向星的加边操作(add_edge),和邻接表,邻接矩阵一样,这就是增加一条由 u 指向 v 的边的操作,如果是带权边,则边权就是w
链式前向星的数据结构:
const int N=10005;
struct Edge
{int to,w,next;
}edge[N];
int head[N],cnt;
如上,我们使用一个结构体和两个变量便可以描绘出链式前向星
结构体:
- to 代表这条边的终点
- w 代表这个边的权值(如果是带权边)
- next 代表与这条边起点相同的上一条边的编号
- head 代表head[i],以i为起点的最后一条边的编号
- cnt 代表边的数量
这个next到底是什么意思???
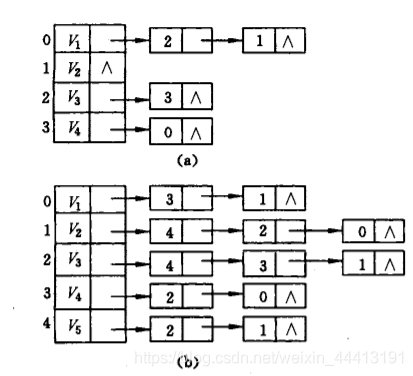
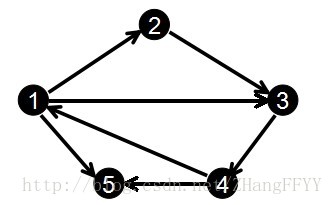
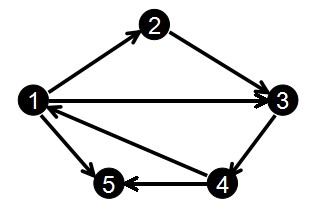
看这个图:3的next 就表示与3的起点1为起点,的上一条边的编号是 2
如果这是一个树结构,则就表示的是当前节点的兄弟节点,不过是最近的,所以是以这条边的起点相同的上一条边的编号

head的含义:
head数组始终记录以 1 为起点的最后一条边的编号,图中操作完成后 head[1]=3

表示 以 1 作为起点的最后一条边的编号,
- 2号节点连接时,head[1] 表示 2号节点;
- 3节点进入后,head[1]表示3号节点。
接下来我们就来解析 上面那段函数代码
void add_edge(int u, int v, int w)
{edge[cnt].to = v; //终点为vedge[cnt].w = w; //边权edge[cnt].next = head[u]; //以u为起点的上一条边的编号为head[u]head[u] = cnt++; //更新以u为起点的最后一条边的编号为cnt
}
- edge[cnt].to = v :添加一条从 u -> v的边
- edge[cnt].w = w:u->v这条边的边权是w
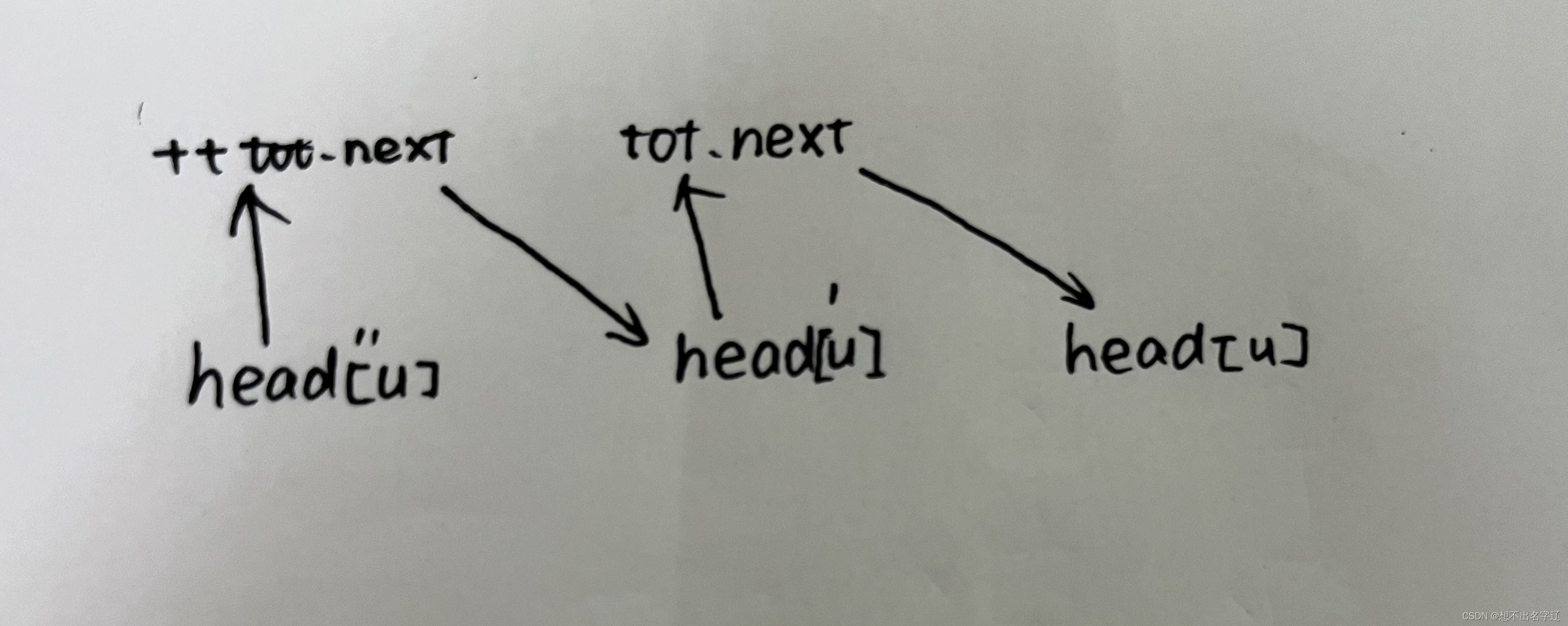
- edge[cnt].next = head[u]:
- edge[cnt].next:表示以 u 为起点的上一条边的编号。
- head[u]:以u为起点的最后一条边的编号。
- 连起来就表示:以u为起点的上一条边的编号为 head[u]
- head[u] = cnt++:更新以u为起点的最后一条边的编号
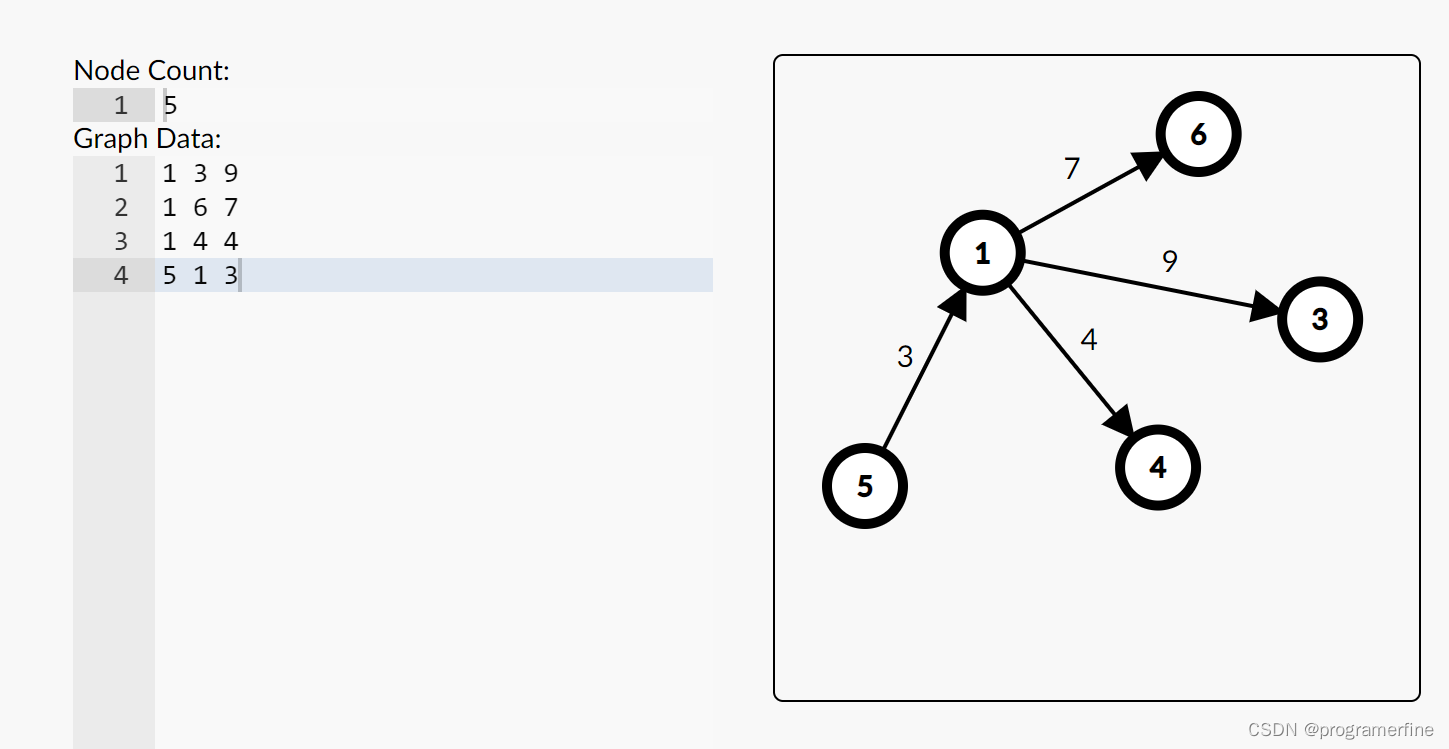
下面我借助例子来说明一下:
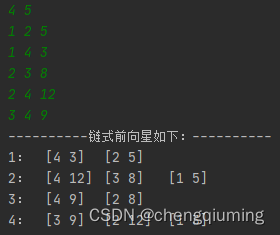
5 7
1 2 1
2 3 2
3 4 3
1 3 4
4 1 5
1 5 6
4 5 7
对于1 2 1这条边:edge[0].to = 2; edge[0].next = -1; head[1] = 0;
对于2 3 2这条边:edge[1].to = 3; edge[1].next = -1; head[2] = 1;
对于3 4 3这条边:edge[2].to = 4; edge[2],next = -1; head[3] = 2;
对于1 3 4这条边:edge[3].to = 3; edge[3].next = 0; head[1] = 3;
对于4 1 5这条边:edge[4].to = 1; edge[4].next = -1; head[4] = 4;
对于1 5 6这条边:edge[5].to = 5; edge[5].next = 3; head[1] = 5;
对于4 5 7这条边:edge[6].to = 5; edge[6].next = 4; head[4] = 6
那么经过我们的努力理解,我们终于明白了这个函数的作用,其实还有另外一种写法:
void add_edge(int u, int v, int w)
{edge[++cnt].to = v; //终点为vedge[cnt].w = w; //边权edge[cnt].next = head[u]; //以u为起点的上一条边的编号为head[u]head[u] = cnt; //更新以u为起点的最后一条边的编号为cnt
}
看出区别了吗,其实就是 第一行的edge的 cnt提前++,其实和上面是一致的,前一个从0开始,这个的话就是从1 开始。
对于初始化,我们直接把head memset 为 -1即可,这样就表示所有起点的最后一条边的编号为 -1,即表示没有边
对于遍历函数:
void show()
{for (int i = 1; i <= n; i++){for (int j = head[i]; j != -1; j = edge[j].next){//1: 6 4 2 cout << i << " -> " << edge[j].to << ": " << edge[j].w << endl;}cout << endl;}
}
由于head[i] 存储了 以i为起点的最后一条边的编号,则我们目前对于 i 所在的边集合进行操作,则 j 表示的就是与 i 相连的边的编号,便可以通过 edge来获得 j 的终点与权值;进而往前寻找以i为起点的上一条边的编号,进而往前遍历到所有连接的边。
main函数怎么写???
init();
scanf("%d%d", &n, &m);
for (int i = 1; i <= n - 1; i++)
{int ui, vi, wi;scanf("%d%d%d", &ui, &vi, &wi);add_edge(ui, vi, wi);add_edge(vi, ui, wi);//建双向无向边
}
注意我们这是 建双向无向边,我们可以只使用一个add_edge来建单向边
完整代码
#include <bits/stdc++.h>
using namespace std;const int N = 10005;
struct Edge
{int to, w, next;//起点,边权,以这条边为起点的上一条边的编号
}edge[N];//边集int n, m;//n个点,m条边
int head[N], cnt;//head[i]表示以i为起点的最后一条边的编号
void init()
{for (int i = 1; i <= N; i++){head[i] = -1;//以i为起点的最后上一条边的编号默认为-1}cnt = 0;
}
void add_edge(int u, int v, int w)
{edge[cnt].to = v; //终点为vedge[cnt].w = w; //边权edge[cnt].next = head[u]; //以u为起点的上一条边的编号为head[u]head[u] = cnt++; //更新以u为起点的最后一条边的编号为cnt
}
void show()
{for (int i = 1; i <= n; i++){for (int j = head[i]; j != -1; j = edge[j].next){//1: 6 4 2 cout << i << " -> " << edge[j].to << ": " << edge[j].w << endl;}cout << endl;}
}void test1()
{cin >> n >> m;init();for (int i = 1; i <= n-1; i++){int u, v, w;cin >> u >> v >> w;add_edge(u, v, w); //}show();
}int nxt[N], to[N], val[N];//这是一堆建边要用的东西qaq
void add_edge2(int u, int v, int w)//邻接链表建边..貌似没什么好说的
{nxt[++cnt] = head[u];head[u] = cnt;to[cnt] = v;val[cnt] = w;
}
void test2()
{init();scanf("%d%d", &n, &m);for (int i = 1; i <= n - 1; i++){int ui, vi, wi;scanf("%d%d%d", &ui, &vi, &wi);add_edge2(ui, vi, wi);add_edge2(vi, ui, wi);//建无向边 }
}
int main()
{/*5 21 3 11 4 102 3 203 5 20*/test2();return 0;
}................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................