在dalao的压迫下本蒟蒻发个博客，给大家讲一下链式前向星（新手，写错了轻喷）

首先说明一点链式前向星适合于稀疏图，而邻接矩阵则更适合稠密图，所以最好看好数据范围再决策使用哪个方法，当然有些题会刚好卡上美滋滋。

我用数组来写一下

int v[M],w[M],fst[N],nxt[M],idx

其中

idx是该边的编号

v数组表示这条边的终点(v[idx]：表示编号为idx的边的终点）

下标：边的编号，存值含义：点（的编号）

w数组表示这条边的权值(道理跟v数组一样)

下标：边的编号，存值含义：边（的权值）

fst数组表示以这个点为首的最第一条边的编号（不断更新，fst[i]表示以i点起点的第一条边）

下标：点的编号，存值含义：边（的编号）

nxt数组表示与这个边有共同起点的上一条边（一边对一边，nxt[idx]表示与idx有同起点的下一条边）

下标：边的编号，存值含义：（下一条）边（的编号）

注:最后一个输入的边反而是第一个，即fst[i]的数值就是最后一个输入的起点为i的边的编号。

---

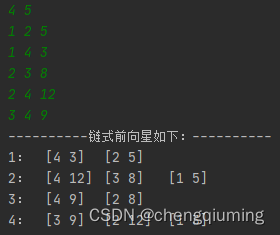
下面是样例：

先推荐一个网页：https://csacademy.com/app/graph_editor/

上代码！复制的！

int fst[N],nxt[M],v[M],w[M],idx=0;
memset(fst,-1,sizeof(fst));//初始化
//          起点   终点  权值
void add(int a,int b,int c){v[++idx]=b;     //终点w[idx]=c;       //权值nxt[idx]=fst[a] //该边(idx)的下一条边就是fst[a](目前的第一条边)fst[a]=idx;     //该点第一条边(不断刷新,该边成为了以这点为起点的第一条边)
}

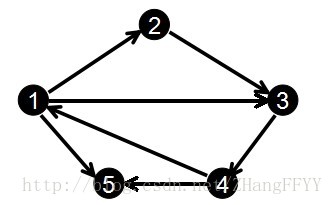
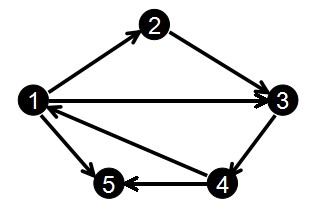
以这个图为例：

 

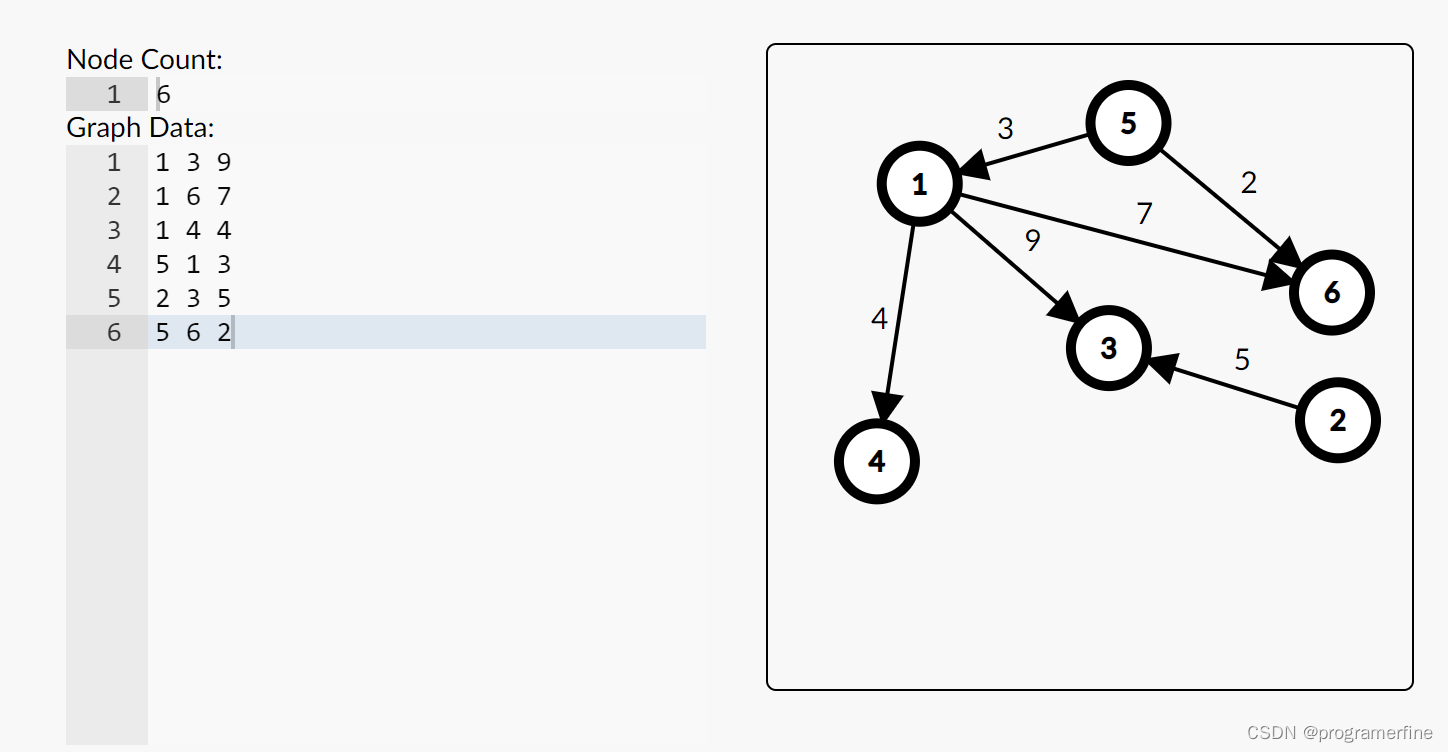
 首先输入1 3 9:

 

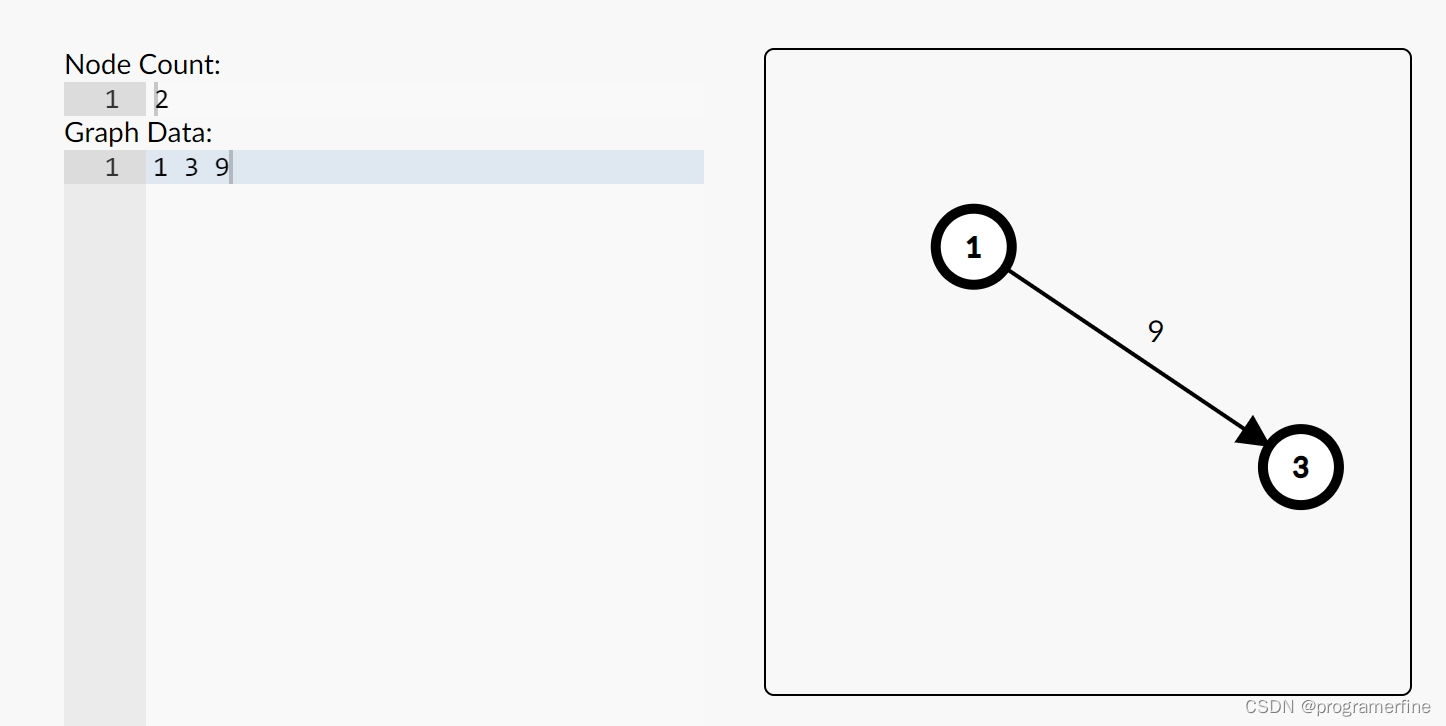
 1->9

v[1]=3

w[1]=9

nxt[1]=-1

fst[1]=1

1 6 7

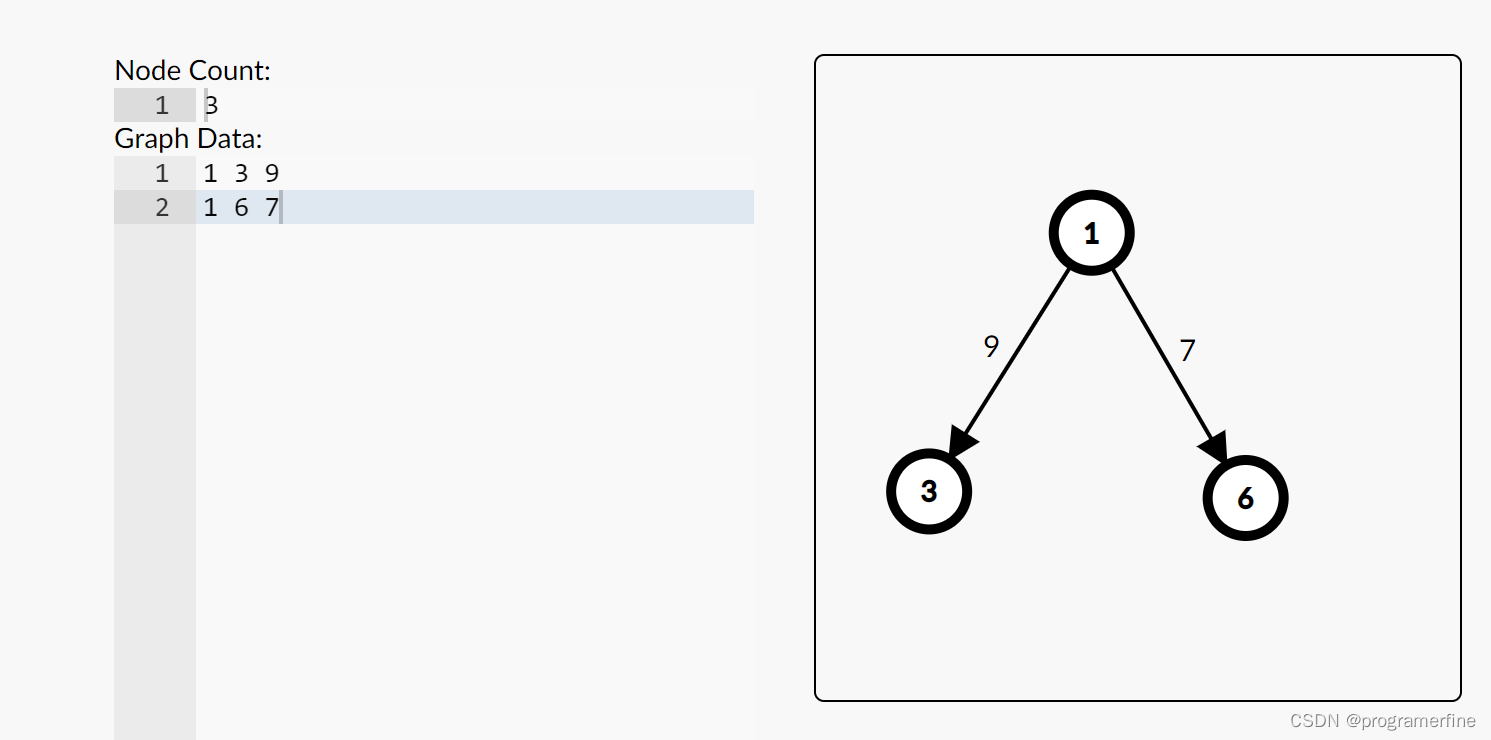
1->6

v[2]=6

w[2]=7

 nxt[2]=1

fst[1]=2

1 4 4

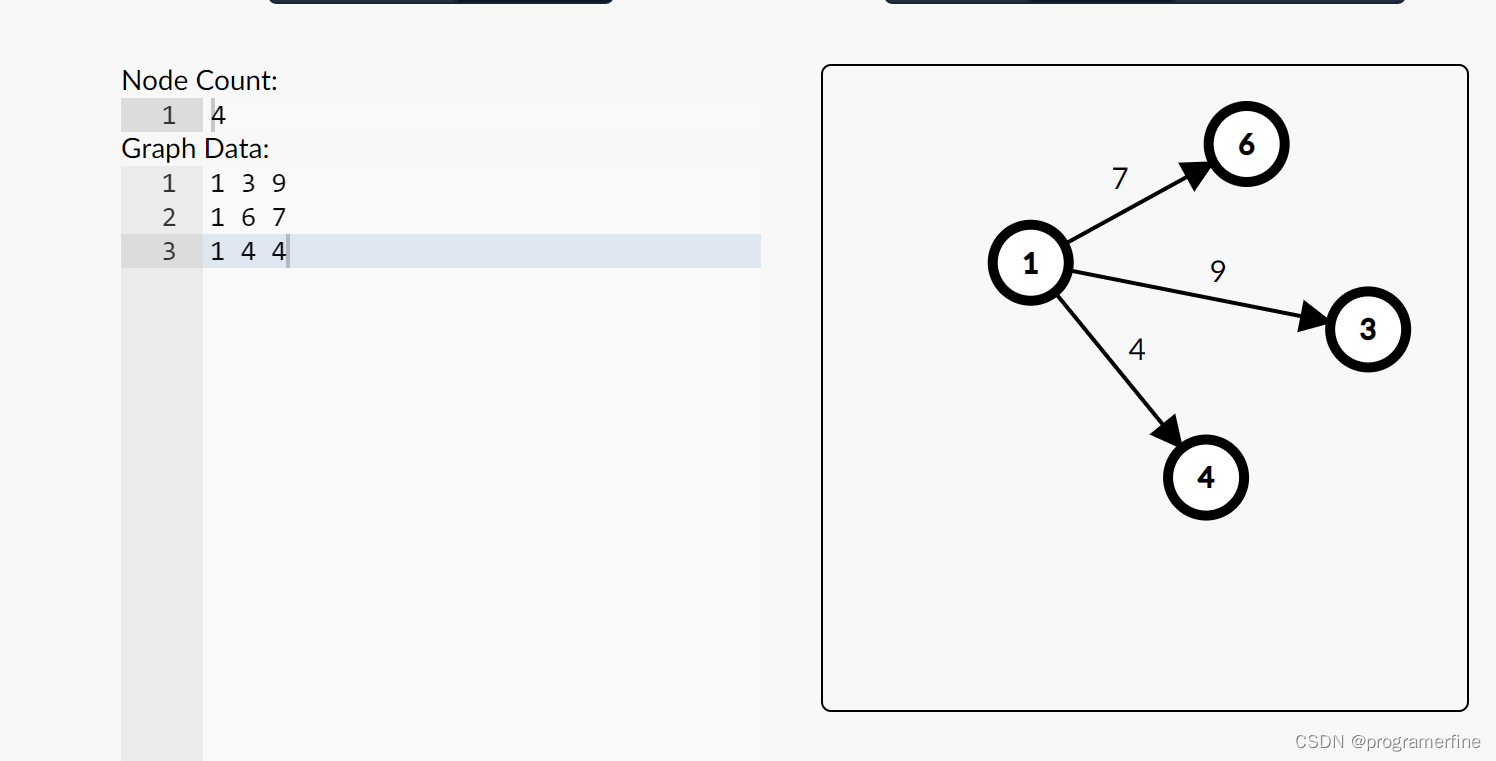
1->4

v[3]=4

w[3]=4

nxt[3]=2

fst[1]=3

 

5 1 3

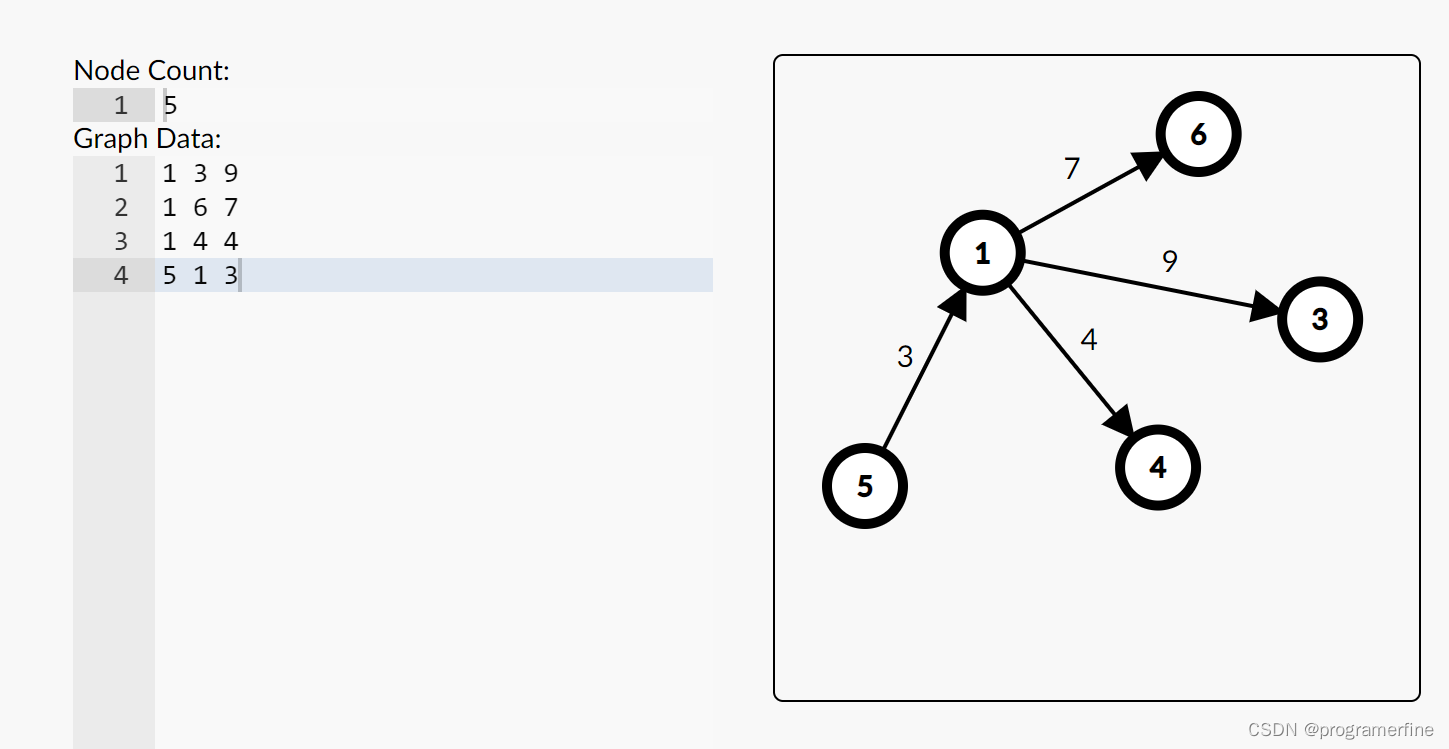
 v[4]=1

w[4]=3

nxt[4]=-1

fst[5]=4

以此类推......

---

链式前向星的遍历：

//进行一个历的遍(bushi
for(int i=1;i<=n;i++){
//从第一个以x为起点的边开始  判断j是否为-1  遍历下一条以x为起点的边for(int j=fst[x];~j;j=nxt[j]){//进行操作}
}

顺便略讲一下存边操作

//x:起始点（父亲）
//y:终点（孩子）
//z:边的权值
cin>>x>>y>>z;
add(x,y,z);
//如果是无向图,可以近似理解a和b之间的边由两个有向的边:a->b b->a构成
add(y,x,z);

真的太逊了xs（笑死）