图的遍历方法

article/2025/10/28 8:04:30

从图中某一顶点出发访遍图中其余顶点，且使每一个顶点仅被访问一次，这一过程就叫做图的遍历（Traversing Graph）

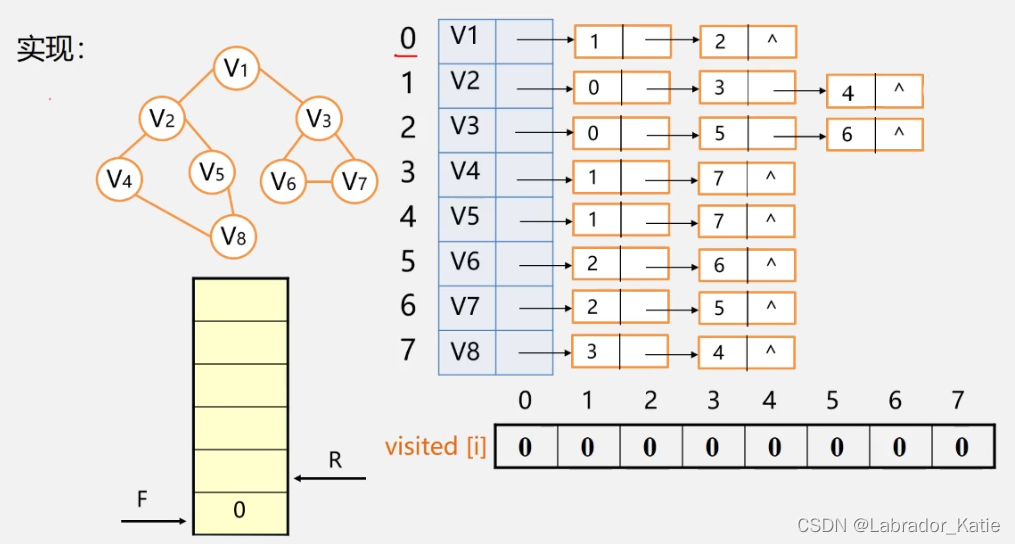
访问过的顶点打上标记，避免访问多次而不自知；可以通过设置一个访问数组visited[n]，n是图中顶点个数，初值为0，访问之后设置为1

图遍历要避免因回路陷入死循环，通常有两种遍历次序方案：

深度优先遍历
广度优先遍历

深度优先遍历

深度优先遍历（Depth_First_Search），也有称为深度优先搜索，简称DFS

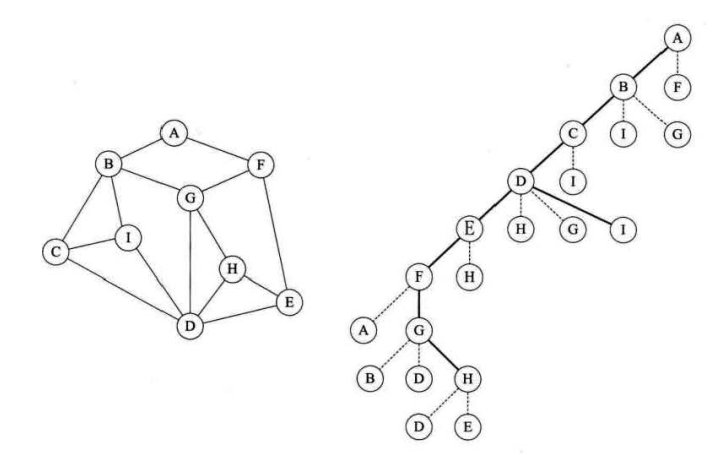
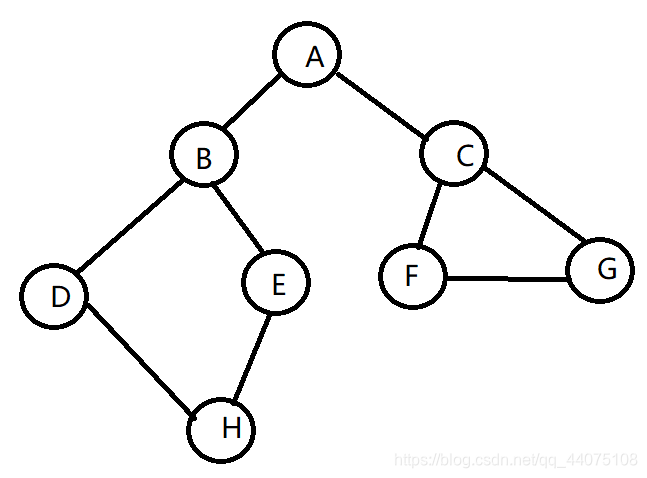
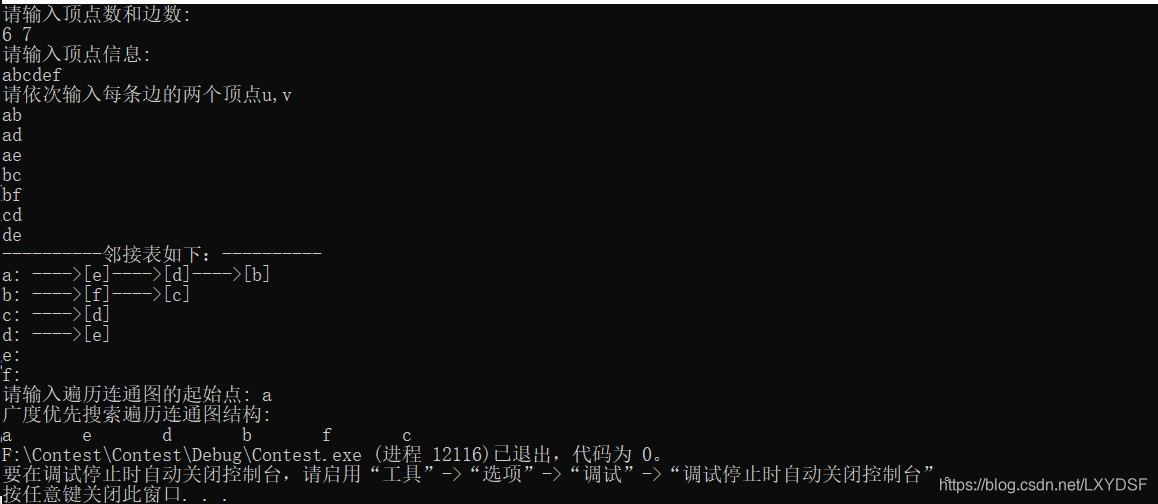
如上图，如何从顶点A开始走遍所有的图顶点并作上标记？

从顶点A开始，始终向右手边走，注意，走到最后，还有一个I顶点没走。

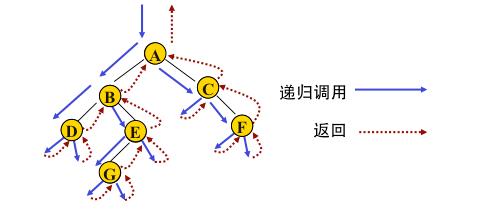
深度优先遍历其实就是一个递归的过程，从图右边路径可以看出类似一棵树的前序遍历，确实如此。

从图中某个顶点v出发，访问此顶点，然后从v的未被访问的邻接点出发深度优先遍历图，直至图中所有和v有路径想通的顶点都被访问到。

非连通图，只需要对它的连通分量分别进行深度优先遍历，即在先前一个顶点进行一次深度优先遍历后，若图中尚有顶点未被访问，则选图中一个未被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。

邻接矩阵深度优先遍历

邻接矩阵表示如下图：

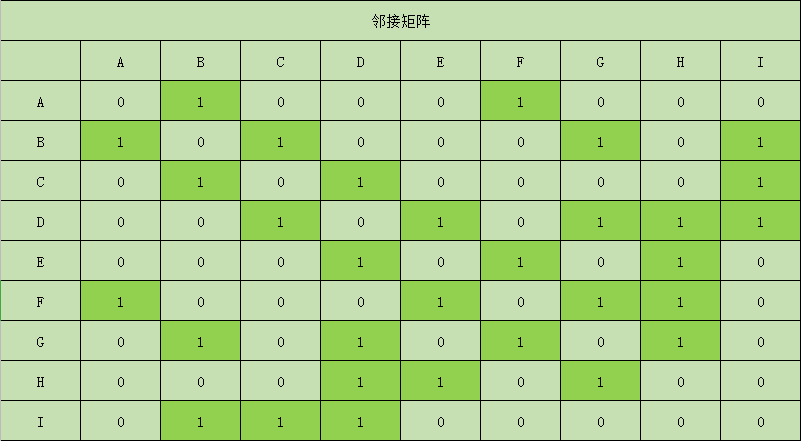
/*** 邻接矩阵的深度优先遍历（注意I点的遍历比较特殊）* @author jiaxinxiao* @date 2019年12月28日*/
public class DFSTest {Boolean[] visited = new Boolean[9];//邻接矩阵的深度优先递归算法void DFS(Graph graph,int i){int j;visited[i] = true;System.out.println(graph.verxs[i]);//打印顶点,也可以进行其他操作for(j = 0;j<graph.numVertexes;j++){if(graph.arc[i][j] == 1 && !visited[j]){DFS(graph, j);}}}//邻接矩阵的深度遍历操作void DFSTraverse(Graph graph){int i;for(i = 0;i<graph.numVertexes;i++){visited[i] = false;//初始化所有顶点状态都是未访问状态}for(i=0;i<graph.numVertexes;i++){if(!visited[i]){//对未访问过的顶点调用DFS，若是连通图，则只会执行一次DFS(graph, i);}}}
}

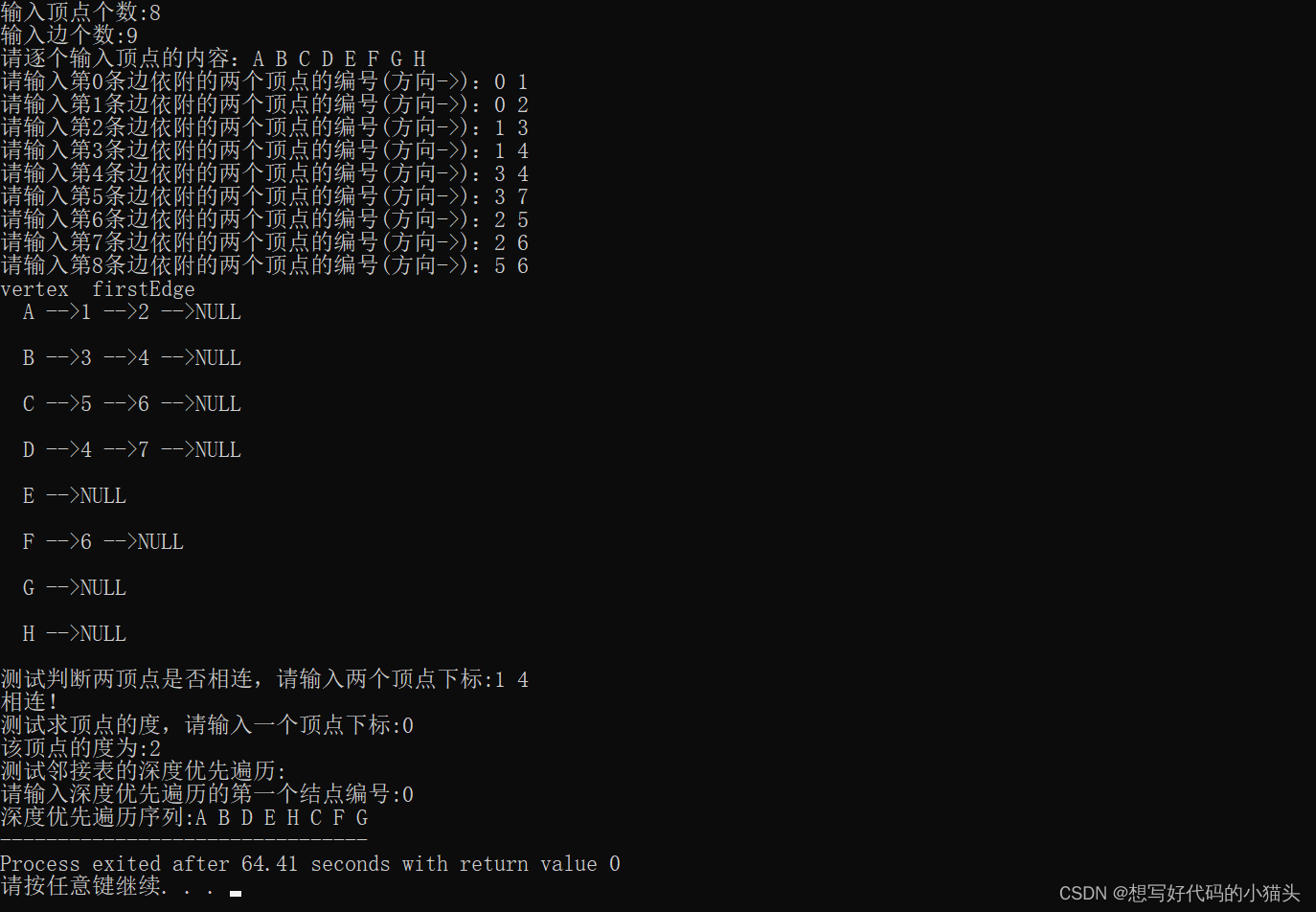
邻接表深度优先遍历

//邻接表深度优先递归算法void DFS(GraphAdjList gl,int i){EdgeNode p = null;visited[i] = true;System.out.println(gl.vertexNodes[i].data);//打印顶点p = gl.vertexNodes[i].firstEdge;while(p != null){if(!visited[p.next.adjvex]){DFS(gl, p.next.adjvex);}p = p.next;}}//邻接表的深度遍历操作void DFSTraverse(GraphAdjList gl){int i;for(i = 0;i<gl.numVertexes;i++){visited[i] = false;//初始化所有顶点状态都是未访问状态}for(i=0;i<gl.numVertexes;i++){if(!visited[i]){//对未访问过的顶点调用DFS，若是连通图，则只会执行一次DFS(gl, i);}}}

总结：两个不同存储结构深度优先遍历算法

邻接矩阵是二维数组，要查找每个顶点的邻接点需要访问矩阵中的元素，因此需要O(n^2)的时间
邻接表做存储结构，需要时间取决于顶点和边的数量，所以是O(n+e)

显然对于点多边少的稀疏图来说，邻接表结构使得算法在时间效率上大大提高。

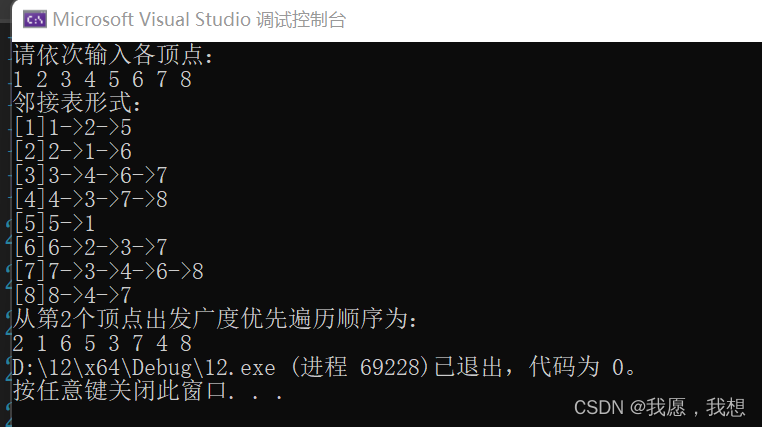
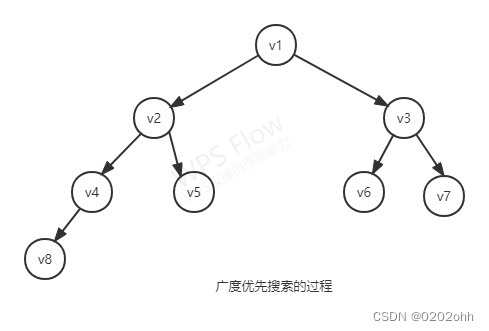
广度优先遍历

广度优先遍历（Breadth First Search），又称广度优先搜索，简称BFS。

深度优先遍历未必是最佳方案，它意味着要彻底查找完一个地方，然后才查找另一个地方。

DFS类似于树的前序遍历，BFS类似于树的层序遍历。

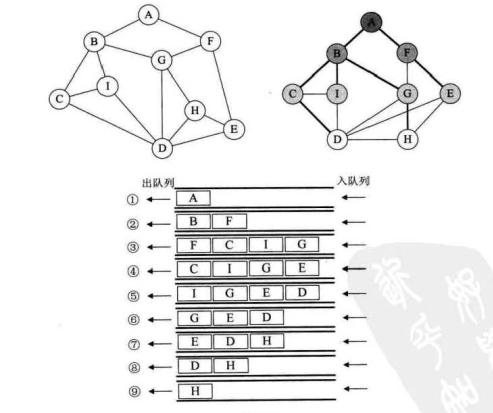
如上图所示，顶点A作为第一层，A的所有边顶点BF作为第二层，BF的所有边顶点CIGE作为第三层，依次类推。

邻接矩阵广度优先遍历

//邻接矩阵广度遍历算法
void BFSTraverse(Graph g){int i,j;Queue<Integer> q;for(i=0;i<g.numVertexes;i++){visited[i] = false;}q = new LinkedList<Integer>();for(i=0;i<g.numVertexes;i++){if(!visited[i]){//未访问就处理visited[i] = true;System.out.println(g.verxs[i]);//打印顶点q.offer(i);//此顶点入队while(!q.isEmpty()){//若当前队列不为空i = q.poll();//出队并记录此顶点在数组中的下标for(j=0;j<g.numVertexes;j++){//判断其他顶点若与当前顶点存在边，并且从未访问过if(g.arc[i][j] == 1 && !visited[j]){visited[j] = true;//打印顶点System.out.println(g.verxs[j]);//将找到的顶点入队列q.offer(j);}}}}}
}

邻接表广度优先遍历

//邻接表广度遍历算法
void BFSTraverse(GraphAdjList g){int i;EdgeNode p;Queue<Integer> q;for(i=0;i<g.numVertexes;i++){visited[i] = false;}q = new LinkedList<Integer>();for(i=0;i<g.numVertexes;i++){if(!visited[i]){visited[i] = true;//打印顶点System.out.println(g.vertexNodes[i].data);q.offer(i);while(!q.isEmpty()){i = q.poll();//找到当前顶点边表链表头指针p = g.vertexNodes[i].firstEdge;while(p != null){if(!visited[p.adjvex]){visited[p.adjvex] = true;System.out.println(g.vertexNodes[p.adjvex].data);q.offer(p.adjvex);}p = p.next;//指针指向下一个邻接点}}}}
}