一、定义

从给定图中任意指定的顶点（称为初始点）出发，按照某种搜索方法沿着图的边访问图中所有顶点，使每个顶点仅被访问一次，这个过程称为图的遍历。如果给定图是连通的无向图或者是强连通的有向图，则遍历过程一次就能完成，并可按访问的先后顺序得到由该图的所有顶点组成的一个序列。

二、方法

在遍历的过程中，从图的初始点到达图中的每个顶点可能存在多条路径。当沿着图中的一条路径访问过某顶点之后，可能还沿着另一条路径回到该顶点，即存在回路。为了避免同一个顶点被重复访问，需要设置一个访问标记数组visited，当顶点i，被访问过时，数组中的元素visited[i]置为1，否则置为0。
图的遍历过程实际就是搜索过程，根据搜索方法的不同，图的遍历方法有两种：一种是深度优先遍历，另一种叫广度优先遍历。

1、深度优先遍历

深度优先遍历的过程是从图中的某个初始点v出发，首先访问初始点v，然后选择一个与顶点v相邻且没被访问过的顶点w，以w为初始顶点，再从它出发进行深度优先遍历，直到图中与顶点v邻接的所有顶点都被访问为止，显然这是一个递归过程。
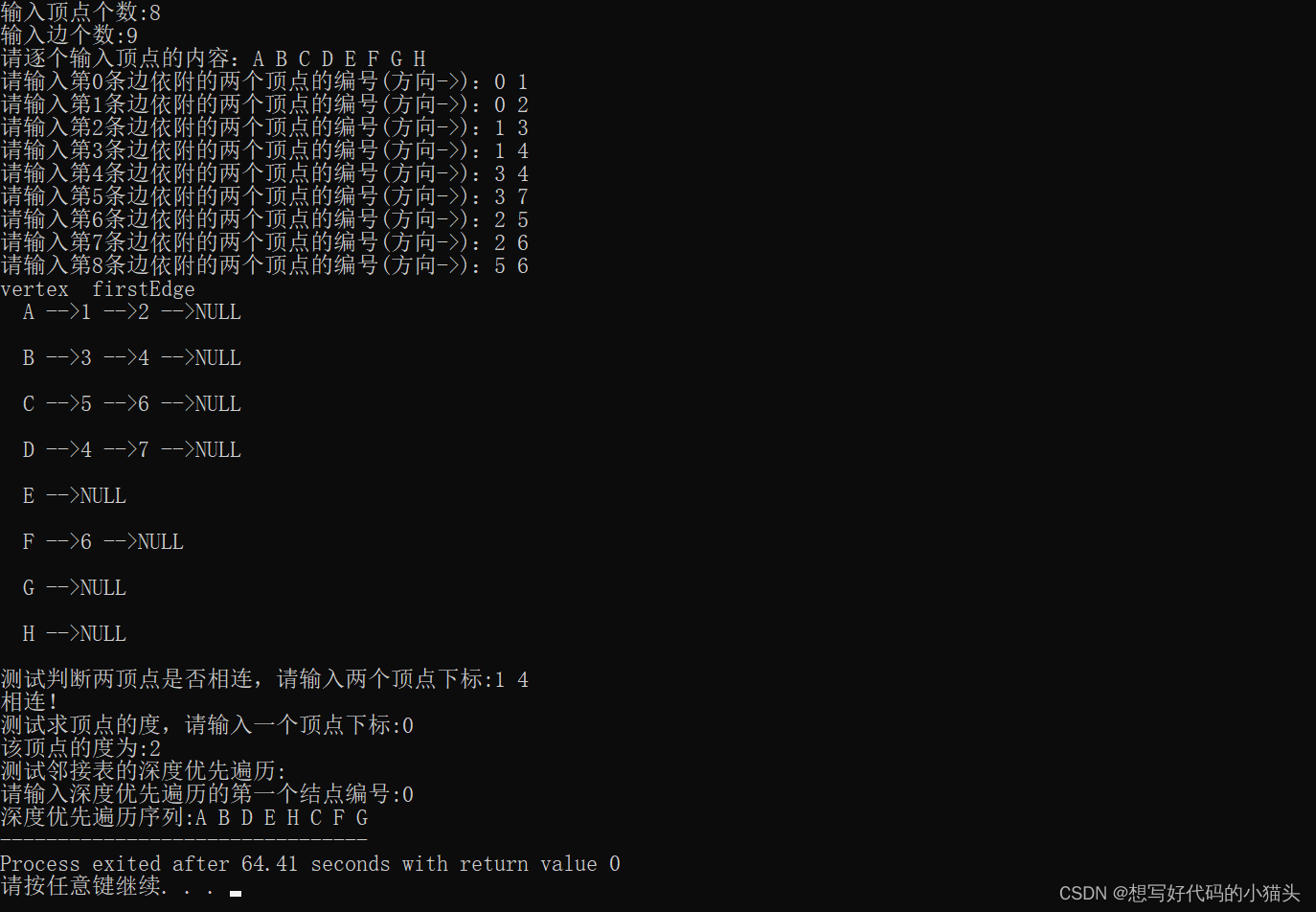
下面给出一个示例：

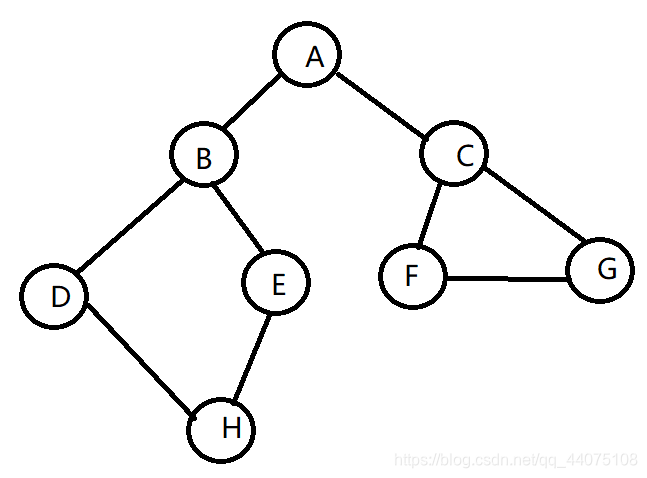
在这里插入图片描述
该图以A为初始点，从左往右通过深度优先遍历可以得到序列：ABDHECFG ，当然如果采取从右往左通过深度优先遍历可以得到序列：ACGFBEHD，可见采用深度优先遍历得到的序列并不是唯一的，这与建图时的存储有关，假如采用邻接表来存储，当每个顶点的邻接顶点采用头插法插入，那么之后采用深度优先遍历进行遍历时就会得到序列ACGFBEHD，当每个顶点的邻接顶点采用尾插法插入，那么之后采用深度优先遍历进行遍历就得到序列ABDHECFG。
下面来看看深度优先遍历的代码

//深度优先遍历:  g:图  v:初始点    visited:标记数组
void DFS(GraphLnk *g, int v, bool visited[])
{//访问顶点，获取值，打印printf("%c-->",GetVertexValue(g,v));visited[v] = true;//为访问过的顶点做上标记int w = GetFirstNeighbor(g,GetVertexValue(g,v));//获取第一个邻接顶点while(w != -1){//当邻接顶点未被访问if(!visited[w]){DFS(g,w,visited);//以该顶点为起始顶点进行深度优先遍历}/*对第一个邻接顶点深度优先遍历完成，获取下一个邻接顶点的位置（如果该顶点未被访问，那么下一轮将以该顶点为起始顶点进行深度优先遍历）*/w = GetNextNeighbor(g,GetVertexValue(g,v),GetVertexValue(g,w));}
}

2、广度优先遍历

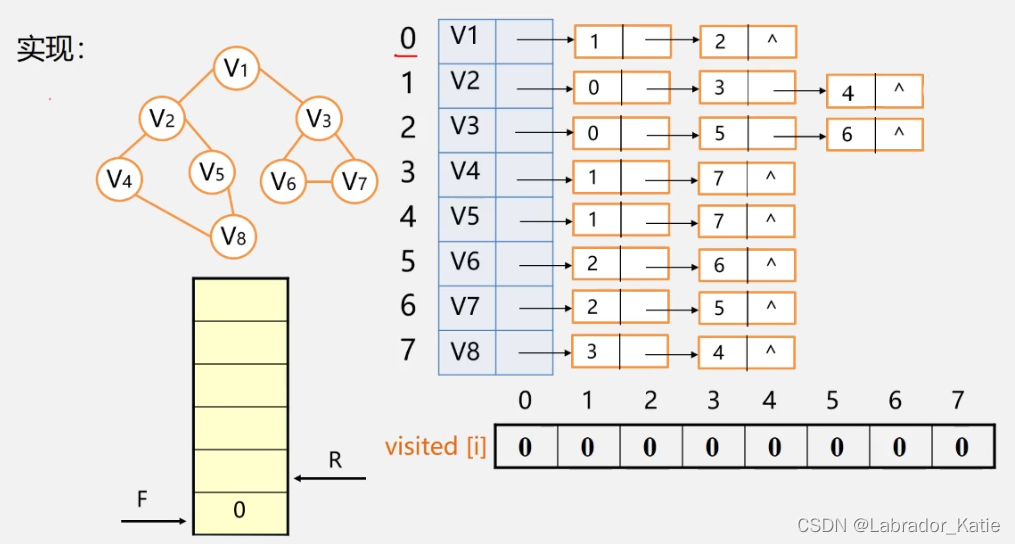
广度优先遍历的过程是首先访问初始点v，接着访问顶点v的所有未被访问过的邻接点v1，v2，v3，…，vt，然后再按照v1，v2，v3，…，vt的次序访问每一个顶点的所有未被访问过的邻接点，依此类推，直到图中所有和初始点v有路径相通的顶点都被访问过为止。为了实现红色部分描述的先访问顶点的邻接顶点先访问，需要借用队列来实现。
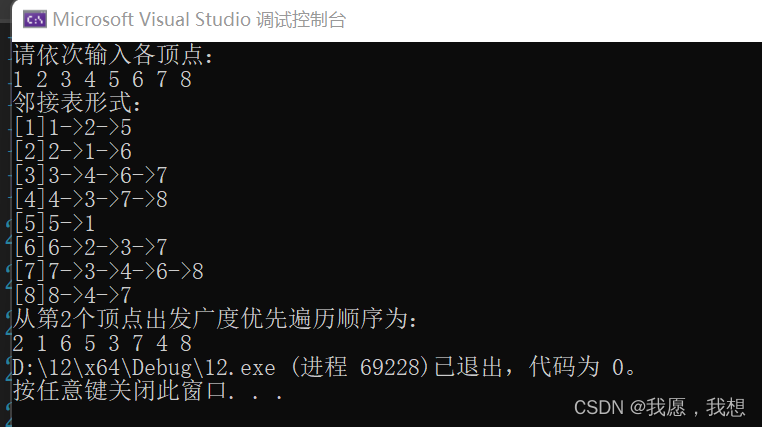
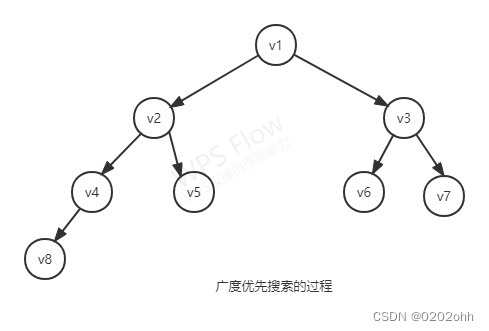
下面给出一个示例：

在这里插入图片描述
该图以A为初始点，从左往右通过广度优先遍历可以得到序列：ABCDEFGH ，当然如果采取从右往左通过广度优先遍历可以得到序列：ACBGFEDH，可见采用广度优先遍历得到的序列也并不是唯一的，原因同深度优先遍历不唯一的原因，此处不再赘述。
下面来看看广度优先遍历的代码

//广度优先遍历：g:图  v:初始点  visited:标记数组
void BFS(GraphLnk *g, int v, bool visited[])
{printf("%c-->",GetVertexValue(g,v));visited[v] = true;LinkQueue Q;//创建链队InitQueue(&Q);//初始化EnQueue(&Q,v);//将起始顶点入队int w;while(!Empty(&Q))//当队内还有顶点{GetHead(&Q,&v);//获取存在在队头的顶点vDeQueue(&Q);//出队//获取第一个邻接顶点w = GetFirstNeighbor(g,GetVertexValue(g,v));while(w != -1)//存在邻接顶点{if(!visited[w])//当该邻接顶点未被访问{//打印值printf("%c-->",GetVertexValue(g,w));visited[w] = true;//标记为已被访问EnQueue(&Q,w);//将该顶点入队，为之后访问该顶点的邻接顶点做铺垫}//获取顶点v的下一个邻接顶点（该邻接顶点的顺序在前面访问过邻接顶点w之后）w = GetNextNeighbor(g,GetVertexValue(g,v),GetVertexValue(g,w));}}
}

三、实现

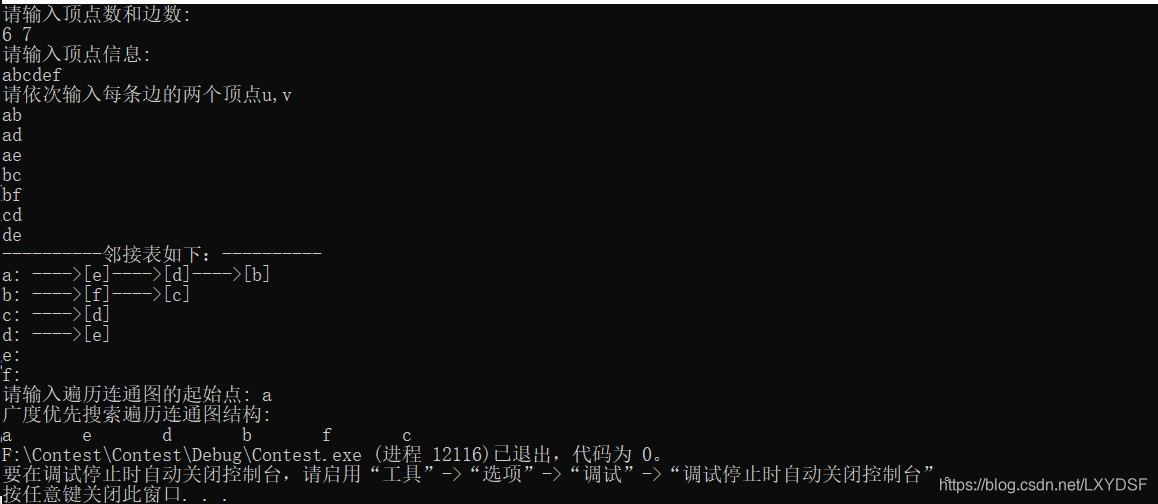
有了上面的理论基础，下面将基于图的邻接表存储来实现图的遍历，如果大家对图的邻接表存储方式还不太理解，那么可以先阅读图之邻接表详解（C语言版）此篇文章之后，再接着往下阅读。

1、无向图或强连通有向图遍历

如果给定图是连通的无向图或者是强连通的有向图，则遍历过程一次就能完成，并可按访问的先后顺序得到由该图的所有顶点组成的一个序列。

深度优先遍历实现

//深度优先遍历：给出遍历的图g和起始顶点vertex
void DFS(GraphLnk *g, T vertex)
{int n = g->NumVertices;//获取顶点个数//根据顶点数建立辅助数组空间：用来标记哪些顶点已经访问过，哪些顶点没有访问bool *visited = (bool*)malloc(sizeof(bool) * n);assert(visited != NULL);for(int i=0; i<n; ++i)//初始化标记数组{visited[i] = false;}//获取起始节点在邻接表中的位置int v = GetVertexPos(g,vertex);DFS(g,v,visited);//遍历free(visited);//释放辅助空间
}

广度优先遍历实现

//广度优先遍历：给出遍历的图g和起始顶点vertex
void BFS(GraphLnk *g, T vertex)
{int n = g->NumVertices;//获取顶点个数//根据顶点数建立辅助数组空间：用来标记哪些顶点已经访问过，哪些顶点没有访问bool *visited = (bool*)malloc(sizeof(bool) * n);assert(visited != NULL);for(int i=0; i<n; ++i)//初始化标记数组{visited[i] = false;}//获取起始顶点在邻接表中的位置int v = GetVertexPos(g,vertex);BFS(g,v,visited);//遍历	free(visited);
}

2、非连通图遍历

如果给定图是非连通图，则只能访问到初始点所在分量中的所有顶点，其他连通分量中的顶点是不可能访问到的，为此需要从其他每个连通分量中选择初始点，分别进行遍历，这样才能够访问到图中的所有顶点。

深度优先遍历实现

//非连通图的深度优先遍历方式
void NonUnicomDFS(GraphLnk *g)
{int n = g->NumVertices;//获取顶点个数//根据顶点数建立辅助数组空间：用来标记哪些顶点已经访问过，哪些顶点没有访问bool *visited = (bool*)malloc(sizeof(bool) * n);assert(visited != NULL);for(int i=0; i<n; ++i)//初始化标记数组{visited[i] = false;}for(i=0; i<n; ++i) //遍历非连通图的顶点{if(!visited[i])//以没有访问的顶点为起始顶点进行深度优先遍历DFS(g,i,visited);}free(visited);
}

广度优先遍历实现

//非连通图的广度优先遍历方式
void NonUnicomBFS(GraphLnk *g)
{int n = g->NumVertices;//获取顶点个数//根据顶点数建立辅助数组空间：用来标记哪些顶点已经访问过，哪些顶点没有访问bool *visited = (bool*)malloc(sizeof(bool) * n);assert(visited != NULL);for(int i=0; i<n; ++i)//初始化标记数组{visited[i] = false;}for(i=0; i<n; ++i) //遍历非连通图的顶点{if(!visited[i])//以没有访问的顶点为起始顶点进行广度优先遍历BFS(g,i,visited);}free(visited);
}