一、图的遍历的相关定义

二、深度优先搜索

（一）深度优先搜索连通子图的基本思想

（二）采用递归的形式说明，则深度优先搜索连通子图的基本思想：

（三）树的深度优先遍历

（四）时间复杂度分析

（五）基于邻接矩阵的深度优先遍历

1. 核心代码

2. 演示

3. 完整代码

4. 结果

5. 非连通图的深度优先遍历

6. 完整代码

7. 结果

（六）基于邻接表的深度优先遍历

1. 核心代码

2. 完整代码

3. 结果

4. Data1.txt数据

三、广度优先搜索

（一）基于邻接矩阵的广度优先遍历

1. 演示

2. 核心代码

3. 完整代码

4. 结果

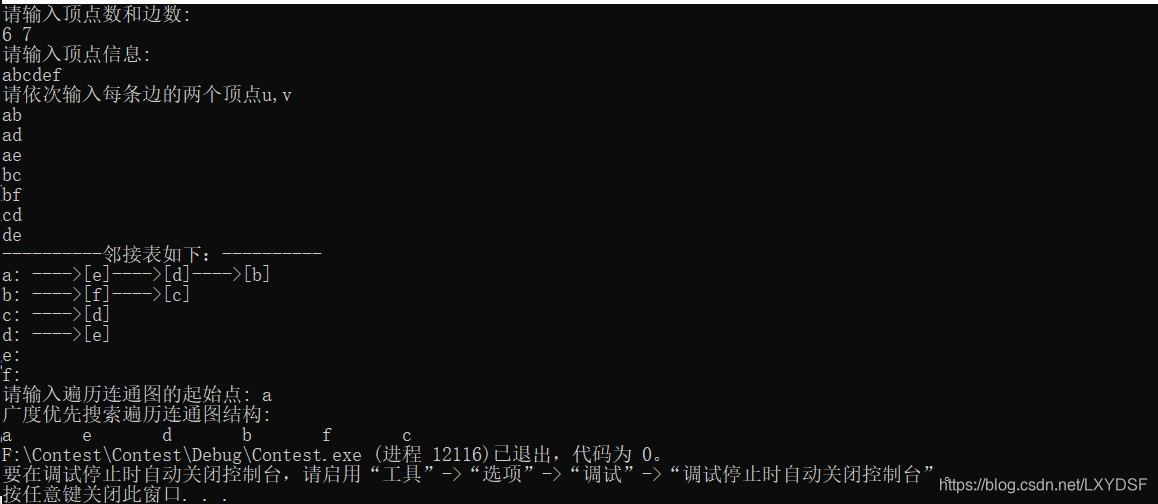
（二）基于邻接表的广度优先遍历

1. 核心代码

2. 完整代码

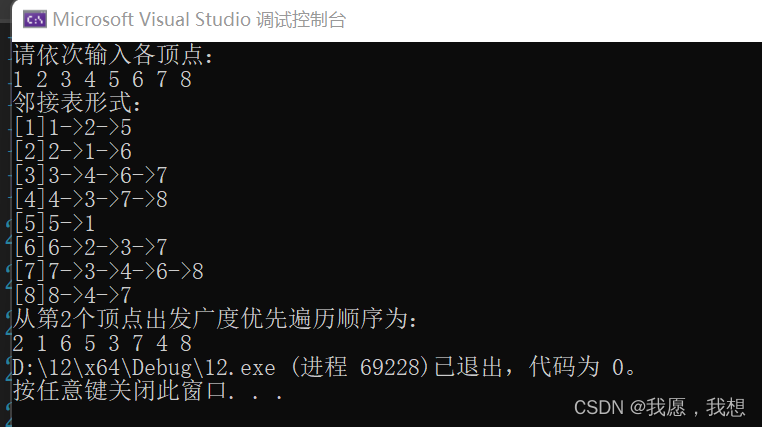
3. 结果

一、图的遍历的相关定义

遍历的定义：从已给的连通图中的某一顶点出发，沿着一些边访遍图中的所有的顶点，且使每个顶点仅被访问一次，就叫做图的遍历，它是图的基本运算。
遍历的实质：找每个邻接点的过程。
图的特点：图中可能存在回路，且图中任一顶点都有可能与其它顶点相通，在访问完某个顶点之后可能会沿着某些边又回到了曾经访问过的顶点。
怎样避免重复访问？
解决思路：设置辅助数组visited[n]，用来标记每个被访问过的顶点。1.初始状态visited[i]为0 ；2.顶点被访问，改visited[i]为1，防止被多次访问

二、深度优先搜索

深度优先搜索（Depth-First Search）是指按照深度方向搜索，它类似于树的先根遍历，是树的先根遍历的推广。

（一）深度优先搜索连通子图的基本思想

从图中某个顶点v0出发，首先访问v0。
找出刚访问过的顶点vi的第一个未被访问的邻接点，然后访问该顶点。以该顶点为新顶点，重复本步骤，直到当前的顶点没有未被访问的邻接点为止。
返回前一个访问过的且仍有未被访问的邻接点的顶点，找出并访问该顶点的下一个未被访问的邻接点，然后执行步骤2

（二）采用递归的形式说明，则深度优先搜索连通子图的基本思想：

访问出发点v0。
依次以v0的未被访问的邻接点为出发点，深度优先搜索图，直至图中所有与v0有路径相通的顶点都被访问。若此时图中还有顶点未被访问，则另选图中一个未被访问的顶点作为起始点，重复上述深度优先搜索过程，直至图中所有顶点均被访问过为止。

（三）树的深度优先遍历

void PreOrder(TreeNode* R)
{if (R != NULL){visit(R);//访问根结点while (R还有下一个子树T){PreOrder(T);//先根遍历下一棵子树}}
}

（四）时间复杂度分析

时间复杂度=访问各个结点所需时间+探索各条边所需时间

邻接矩阵存储的图：
访问 $|V|$ 个顶点需要 $O(|V|)$ 的时间，查找每个顶点的邻接点都需要 $O(|V|)$ 的时间，而且总共有 $|V|$ 个顶点
时间复杂度= $O(|V|^{2})$

邻接表存储的图：
访问 $|V|$ 个顶点需要的时间，查找每个顶点的邻接点共需要 $O(|E|)$ 的时间
时间复杂度= $O(|V|+|E|)$

（五）基于邻接矩阵的深度优先遍历

1. 核心代码

bool visited[MAXV];//访问标记数组
void DFS(MGraph G, int v);//从第v个顶点开始，深度优先遍历
{visit(v);//访问第v个顶点visited[v] = true;//将第v个顶点设置为已经访问的标记for (int w = FirstNeighbor(G, v); w > 0; w = NextNeighbor(G, v, w)){if (!visited[w])//第w个顶点为第v个顶点尚未访问的邻接点{DFS(G, w);}}
}注意;
int FirstNeighbor(MGraph G, int x);//求图G中顶点x的第一个邻接点，若有则返回顶点号；
//若没有邻接点或图中不存在x，则返回-1
int NextNeighbor(MGraph G, int x, int y);
//假设图G中第y个顶点是第x个顶点的一个邻接点，
//返回除第y个顶点之外，第x个顶点的下一个邻接点的顶点号；若第y个顶点是第x个顶点的最后一个邻接点，则返回-1

2. 演示

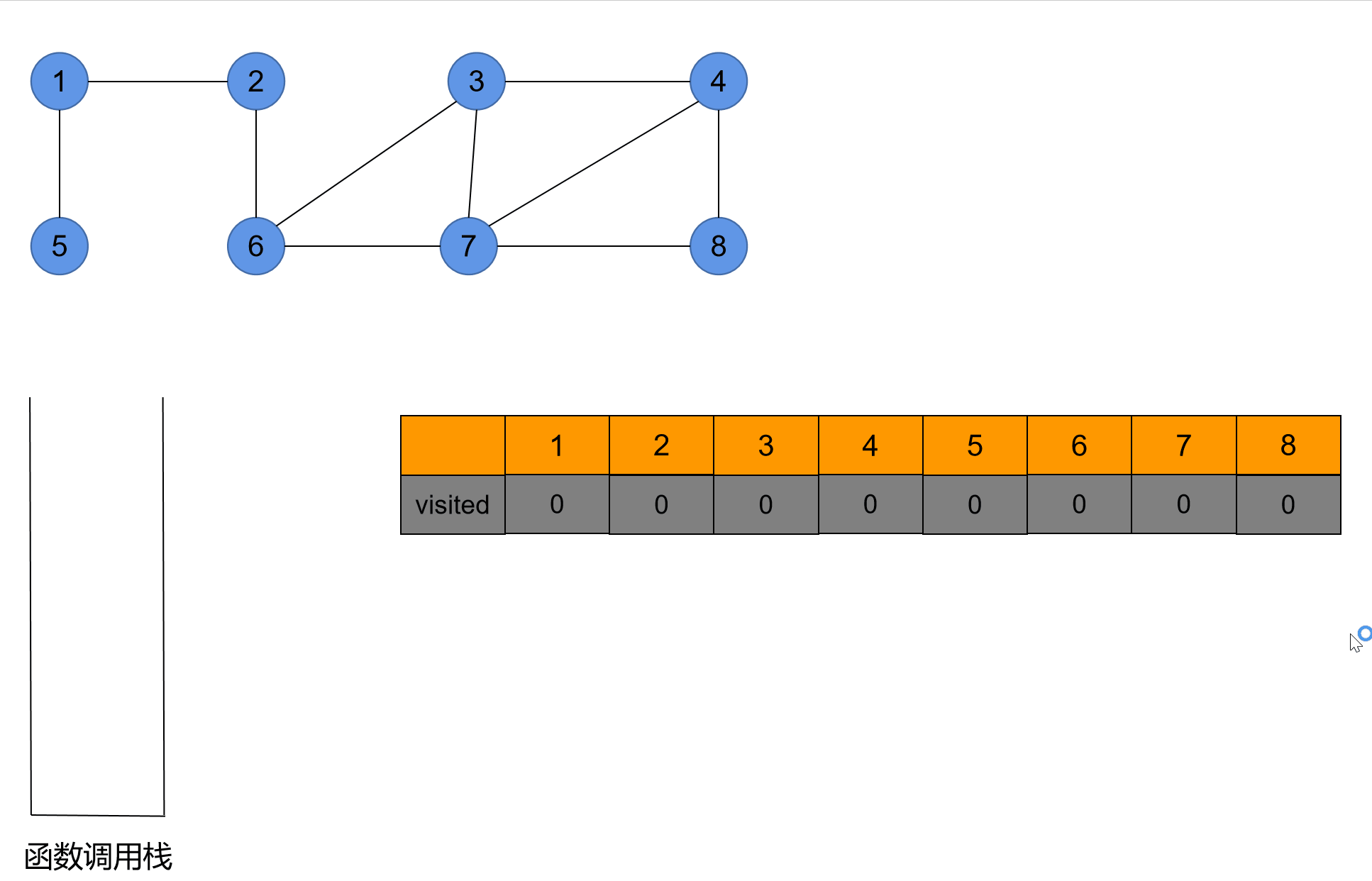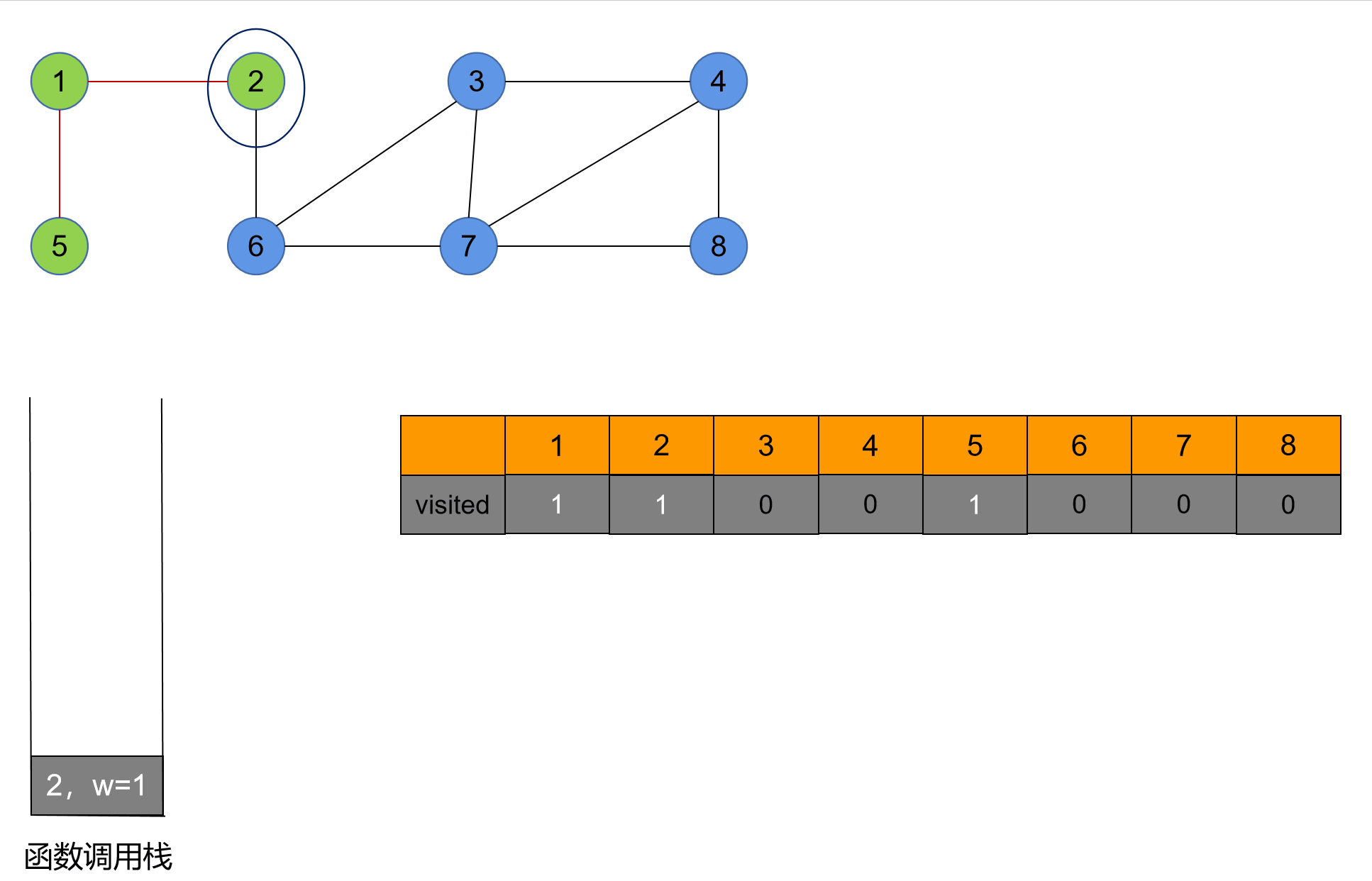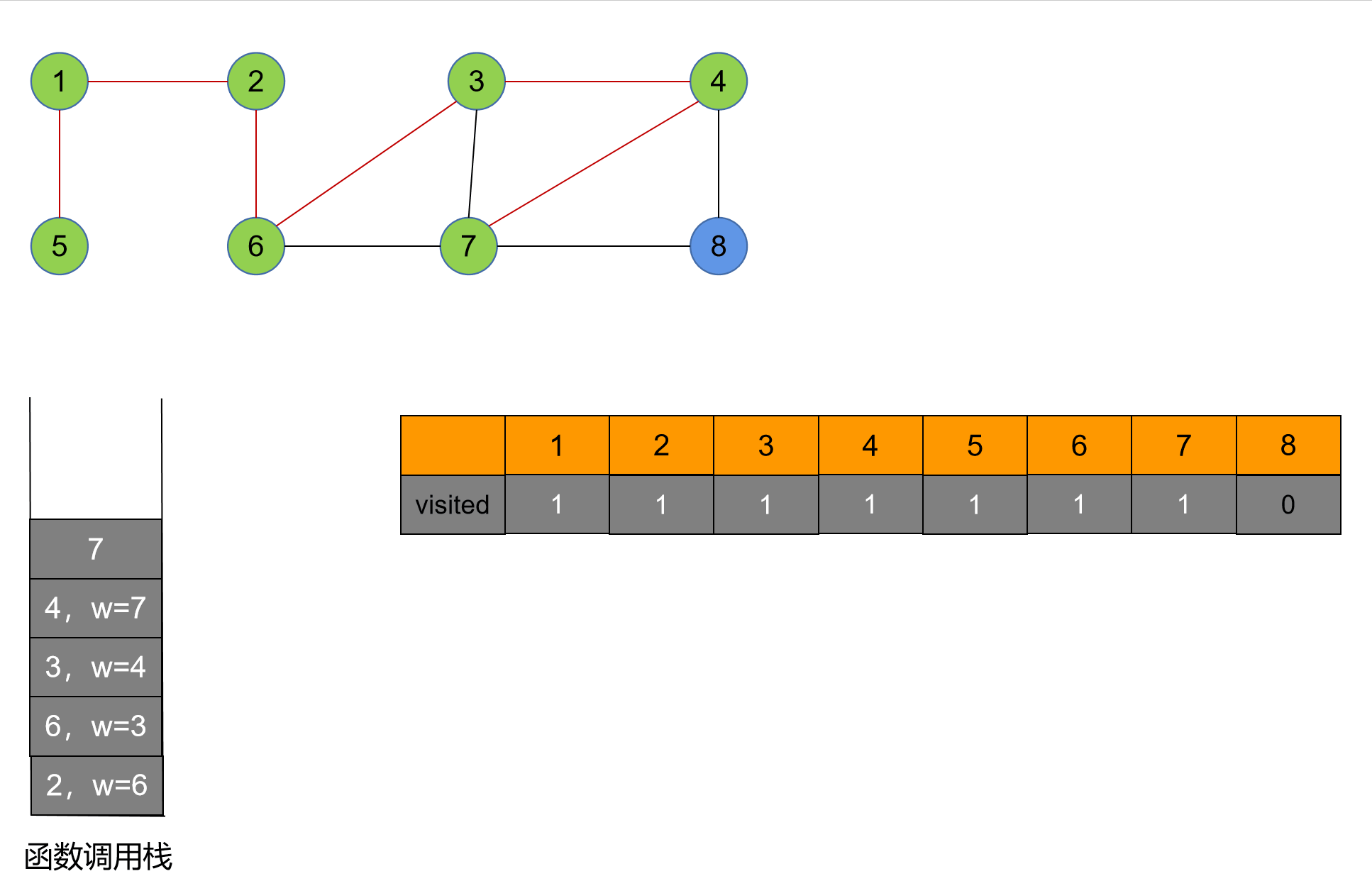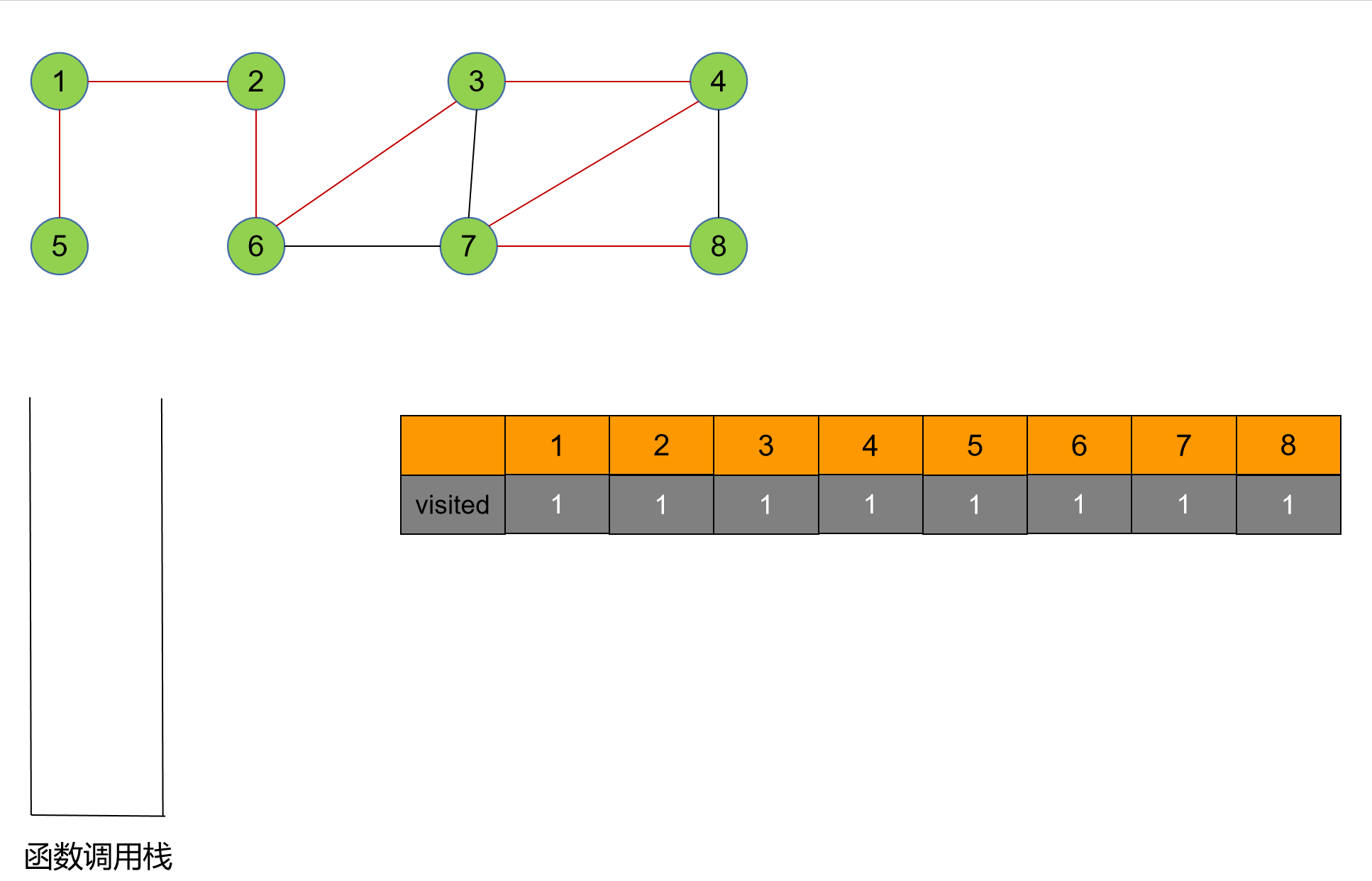
3. 完整代码

MGraph.h

#pragma once
#include<iostream>
#include<stdbool.h>
using namespace std;#define MaxVertexNum 100//顶点数目的最大值
//#define INFINITY  100000//宏定义常量“无穷”
#define MAXV 100typedef int VertexType;//顶点的数据类型
//typedef char VertexType;//顶点的数据类型
typedef int EdgeType;//带权图中边上权值的数据类型
typedef struct
{VertexType vexs[MaxVertexNum];//顶点表（存放顶点）EdgeType edges[MaxVertexNum][MaxVertexNum];//邻接矩阵,边表（存放任意两个顶点之间的距离）int n, e;//图的当前顶点数和边数/弧数
}MGraph;void CreatMat(MGraph& G, int A[][MAXV], int n);//由数组A[n][n]生成邻接矩阵G
//生成图的邻接矩阵方法1
void DisMGraph(MGraph& G);//打印void Init(MGraph& G);//初始化，将所有顶点都初始化为没有访问的顶点
void DFS(MGraph G, int v);//从第v个顶点开始，深度优先遍历
int FirstNeighbor(MGraph G, int x);//求图G中顶点x的第一个邻接点，若有则返回顶点号；
//若没有邻接点或图中不存在x，则返回-1
int NextNeighbor(MGraph G, int x, int y);//假设图G中顶点y是顶点x的一个邻接点，
//返回除y之外顶点x的下一个邻接点的顶点号；若y是x的最后一个邻接点，则返回-1

MGraph1.cpp

#include"MGraph.h"void CreatMat(MGraph& G, int A[][MAXV], int n)//由数组A[n][n]生成邻接矩阵G
{G.n = n;G.e = 0;cout << "请依次输入顶点信息：";for (int i = 1; i <= G.n; i++){cin >> G.vexs[i];}for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){G.edges[i + 1][j + 1] = A[i][j];//i+1，j+1是为了从为了从二维数组[1][1]开始存储if (A[i][j] != 0 && A[i][j] != INFINITY){G.e++;//边数加1}}}
}
void DisMGraph(MGraph& G)//遍历打印
{for (int i = 1; i <= G.n; i++){for (int j = 1; j <= G.n; j++){cout << G.edges[i][j] << " ";}cout << endl;}
}bool visited[MAXV];//访问标记数组
void Init(MGraph& G)//初始化
{for (int i = 1; i <= G.n; i++){visited[i] = false;//标记为访问}
}void DFS(MGraph G, int v)//从第v个顶点(下标也是v)开始，深度优先遍历
{cout << G.vexs[v] << " ";//访问第v个顶点visited[v] = true;//将第v个顶点改为已经访问的标记for (int w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w)){if (!visited[w]){DFS(G, w);}}
}int FirstNeighbor(MGraph G, int x)//求图G中第x个顶点的第一个邻接点，若有则返回顶点号；
//若没有邻接点或图中不存在x，则返回-1
{for (int j = 1; j <= G.n; j++){if (G.edges[x][j] == 1)//寻找第x个顶点的第一个邻接点{return j;//返回第x个顶点的第一个邻接点的顶点号}}return -1;
}
int NextNeighbor(MGraph G, int x, int y)//假设图G中第y个顶点是第x个顶点的一个邻接点，
//返回除第y个顶点之外，第x个顶点的下一个邻接点的顶点号；若第y个顶点是第x个顶点的最后一个邻接点，则返回-1
{int i = 1, j = 1;for (int k = y + 1; k <= G.n; k++)//在邻接矩阵第x个顶点所在行//从第y个顶点之后寻找与第x个顶点邻接的顶点{if (G.edges[x][k] == 1){return k;}}return -1;
}

Text.cpp

#include"MGraph.h"
int main()
{MGraph G;int A[][MAXV] = { {0,1,0,0,1,0,0,0},{1,0,0,0,0,1,0,0},{0,0,0,1,0,1,1,0},{0,0,1,0,0,0,1,1},{1,0,0,0,0,0,0,0},{0,1,1,0,0,0,1,0}, {0,0,1,1,0,1,0,1},{0,0,0,1,0,0,1,0} };CreatMat(G, A, 8);//方法1cout << "图的邻接矩阵：" << endl;DisMGraph(G);cout << endl;/*cout << G.vexs[4] << endl;cout<<FirstNeighbor(G,2)<<endl;cout << NextNeighbor(G, 2, 1);*/Init(G);//初始化cout << "从2出发的深度优先遍历序列：" << endl;DFS(G, 2);cout << endl;Init(G);//初始化cout << "从3出发的深度优先遍历序列：" << endl;DFS(G, 3);//cout << endl;//Init(G);//初始化//cout << "从1出发的深度优先遍历序列：" << endl;//DFS(G, 5);return 0;
}

4. 结果

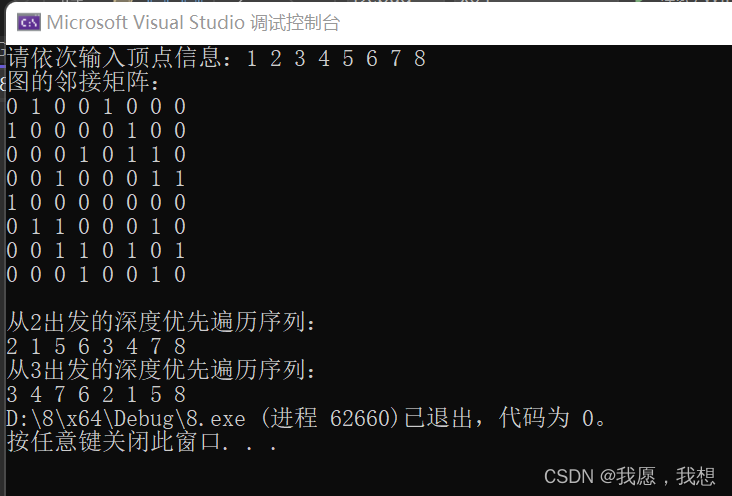
5. 非连通图的深度优先遍历

void DFSTraverse(MGraph G)//对图G进行深度优先遍历
{Init(G);//初始化for (int v = 1; v <= G.n; v++){if (!visited[v])//对每个连通分量调用一次DFS{DFS(G, v);}}
}

6. 完整代码

#pragma once
#include<iostream>
#include<stdbool.h>
using namespace std;#define MaxVertexNum 100//顶点数目的最大值
//#define INFINITY  100000//宏定义常量“无穷”
#define MAXV 100typedef int VertexType;//顶点的数据类型
//typedef char VertexType;//顶点的数据类型
typedef int EdgeType;//带权图中边上权值的数据类型
typedef struct
{VertexType vexs[MaxVertexNum];//顶点表（存放顶点）EdgeType edges[MaxVertexNum][MaxVertexNum];//邻接矩阵,边表（存放任意两个顶点之间的距离）int n, e;//图的当前顶点数和边数/弧数
}MGraph;void CreatMat(MGraph& G, int A[][MAXV], int n);//由数组A[n][n]生成邻接矩阵G
//生成图的邻接矩阵方法1
void DisMGraph(MGraph& G);//打印void Init(MGraph& G);//初始化，将所有顶点都初始化为没有访问的顶点
void DFS(MGraph G, int v);//从第v个顶点开始，深度优先遍历
int FirstNeighbor(MGraph G, int x);//求图G中顶点x的第一个邻接点，若有则返回顶点号；
//若没有邻接点或图中不存在x，则返回-1
int NextNeighbor(MGraph G, int x, int y);
//假设图G中第y个顶点是第x个顶点的一个邻接点，
//返回除第y个顶点之外，第x个顶点的下一个邻接点的顶点号；若第y个顶点是第x个顶点的最后一个邻接点，则返回-1
void DFSTraverse(MGraph G);//对图G进行深度优先遍历（图G可以是非连通图）

#include"MGraph.h"void CreatMat(MGraph& G, int A[][MAXV], int n)//由数组A[n][n]生成邻接矩阵G
{G.n = n;G.e = 0;cout << "请依次输入顶点信息：";for (int i = 1; i <= G.n; i++){cin >> G.vexs[i];}for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){G.edges[i + 1][j + 1] = A[i][j];//i+1，j+1是为了从为了从二维数组[1][1]开始存储if (A[i][j] != 0 && A[i][j] != INFINITY){G.e++;//边数加1}}}
}
void DisMGraph(MGraph& G)//遍历打印
{for (int i = 1; i <= G.n; i++){for (int j = 1; j <= G.n; j++){cout << G.edges[i][j] << " ";}cout << endl;}
}bool visited[MAXV];//访问标记数组
void Init(MGraph& G)//初始化
{for (int i = 1; i <= G.n; i++){visited[i] = false;//标记为访问}
}void DFS(MGraph G, int v)//从第v个顶点(下标也是v)开始，深度优先遍历
{cout << G.vexs[v] << " ";//访问第v个顶点visited[v] = true;//将第v个顶点改为已经访问的标记for (int w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w)){if (!visited[w]){DFS(G, w);}}
}int FirstNeighbor(MGraph G, int x)//求图G中第x个顶点的第一个邻接点，若有则返回顶点号；
//若没有邻接点或图中不存在x，则返回-1
{for (int j = 1; j <= G.n; j++){if (G.edges[x][j] == 1)//寻找第x个顶点的第一个邻接点{return j;//返回第x个顶点的第一个邻接点的顶点号}}return -1;
}
int NextNeighbor(MGraph G, int x, int y)//假设图G中第y个顶点是第x个顶点的一个邻接点，
//返回除第y个顶点之外，第x个顶点的下一个邻接点的顶点号；若第y个顶点是第x个顶点的最后一个邻接点，则返回-1
{int i = 1, j = 1;for (int k = y + 1; k <= G.n; k++)//在邻接矩阵第x个顶点所在行//从第y个顶点之后寻找与第x个顶点邻接的顶点{if (G.edges[x][k] == 1){return k;}}return -1;
}void DFSTraverse(MGraph G)//对图G进行深度优先遍历
{Init(G);//初始化for (int v = 1; v <= G.n; v++){if (!visited[v])//对每个连通分量调用一次DFS{DFS(G, v);}}
}

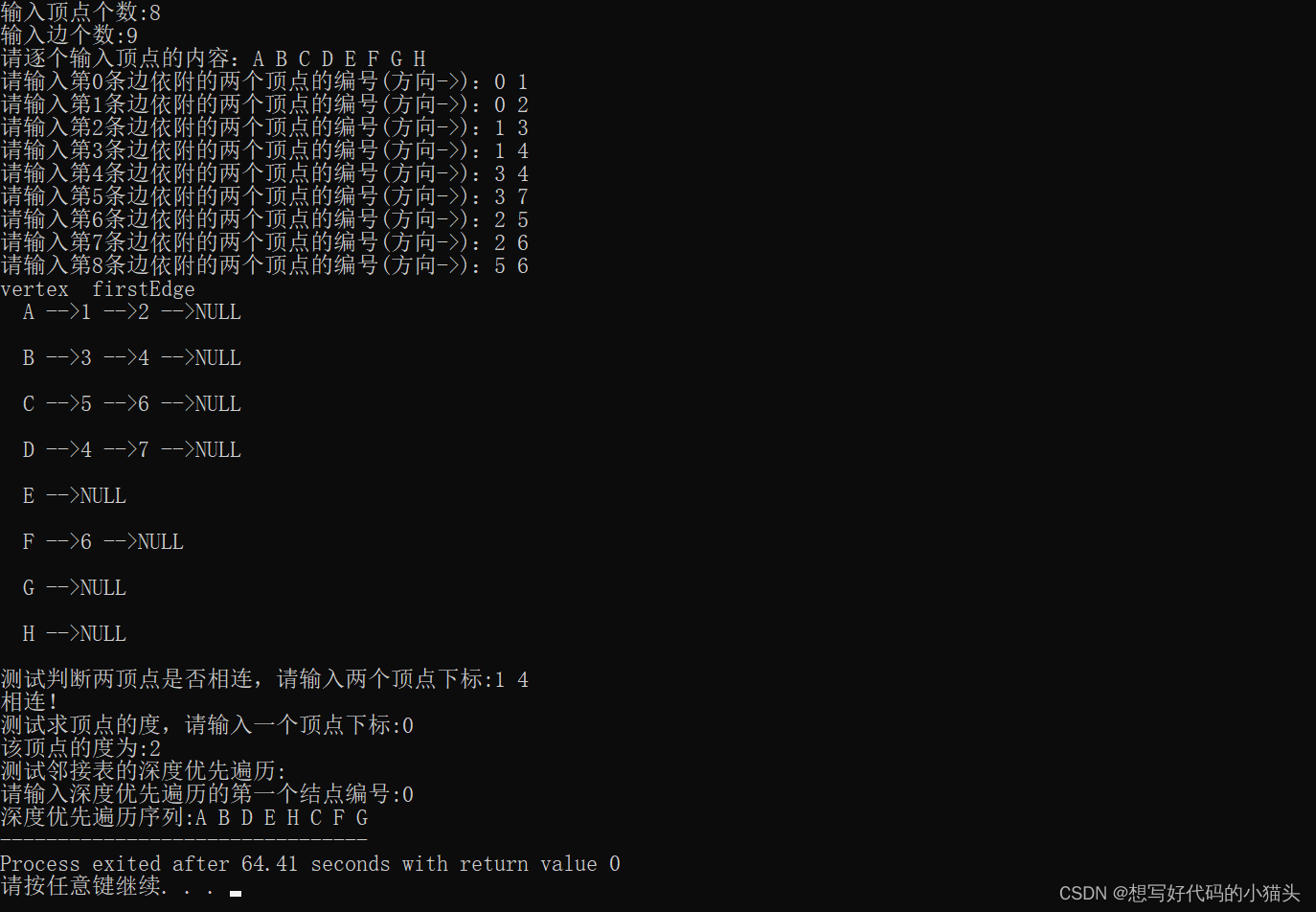
7. 结果

（六）基于邻接表的深度优先遍历

1. 核心代码

int visited[MAXV] = { 0 };
void DFSA(AGraph* G, int i)//邻接表的深度优先算法，i表示从第i个顶点开始深度优先遍历
{ArcNode* p;visited[i] = 1;cout << G->adjlist[i].data<<" ";//访问顶点vip = G->adjlist[i].firstarc;//取vi边表的头指针while (p)//寻找vi的邻接点vj{if (!visited[p->adjvex])//若vj尚且未被访问，则以vj为出发点向纵深搜索{DFSA(G, p->adjvex);}p = p->nextarc;//找vi的下一个邻接点}
}

2. 完整代码

AGraph.h

#pragma once
#include<iostream>
#include<stdbool.h>
using namespace std;//输入流的头文件
#include <cstring>           
#include <io.h>    
#include <fstream>
#define txtRows       8 //txt行数
#define txtCols       8 //txt列数typedef int ElemType;
typedef int InfoType;
#define MAXV 100
#define INF 10000
typedef struct ANode//边结点类型
{int adjvex;//该边的终点位置struct ANode* nextarc;//指向一下条边的指针InfoType info;//该边的相关信息，如带权图可存放权重
}ArcNode;typedef struct Vode//表头结点的类型
{ElemType data;//顶点信息ArcNode* firstarc;//指向第一条边
}VNode;typedef VNode AdjList[MAXV]; //AdjList是邻接表类型
typedef struct
{AdjList adjlist;//邻接表（表头结点组成一个数组）int n, e;//定义顶点数和边数
}AGraph;//图的领接表类型void CreatAdj(AGraph*& G, int A[][MAXV], int n);//由数组A[n][n]生成邻接矩阵G
//生成图的邻接表
void DisAdj(AGraph* G);//打印
void DFSA(AGraph* G, int i);//邻接表的深度优先算法，i表示从第i个顶点开始深度优先遍历

AGraph1.cpp

#include"AGraph.h"void CreatAdj(AGraph*& G, int A[][MAXV], int n)//由数组A[n][n]生成邻接表G
{G = (AGraph*)malloc(sizeof(AGraph));//分配邻接表空间G->n = n;G->e = 0;cout << "请依次输入顶点信息：";for (int i = 1; i <= n; i++)//邻接表的所有表头结点的指针域都设置为空{cin >> G->adjlist[i].data;G->adjlist[i].firstarc = NULL;}ArcNode* p = NULL;for (int i = 0; i < n; i++){for (int j = n - 1; j >= 0; j--){if (A[i][j] != 0 && A[i][j] != INF)//存在一条边{p = (ArcNode*)malloc(sizeof(ArcNode));//创建一个边结点pp->adjvex = j+1;//该边的终点p->info = A[i][j];//该边的权重p->nextarc = G->adjlist[i+1].firstarc;//将新边结点p用头插法插入到顶点Vi的边表头部G->adjlist[i+1].firstarc = p;G->e++;//对于无向图，边数需要除以2}}}
}void DisAdj(AGraph* G)//打印
{ArcNode* p;for (int i = 1; i <= G->n; i++){cout << "[" << i << "]" << G->adjlist[i].data;p = G->adjlist[i].firstarc;//找到顶点i的第一个邻接点while (p != NULL){cout << "->";cout << p->adjvex;p = p->nextarc;//找到下一个邻接点}cout << endl;}
}int visited[MAXV] = { 0 };
void DFSA(AGraph* G, int i)//邻接表的深度优先算法，i表示从第i个顶点开始深度优先遍历
{ArcNode* p;visited[i] = 1;cout << G->adjlist[i].data<<" ";//访问顶点vip = G->adjlist[i].firstarc;//取vi边表的头指针while (p)//寻找vi的邻接点vj{if (!visited[p->adjvex])//若vj尚且未被访问，则以vj为出发点向纵深搜索{DFSA(G, p->adjvex);}p = p->nextarc;//找vi的下一个邻接点}
}

Text.cpp

#include"AGraph.h"
int main()
{int A[MAXV][MAXV];FILE* fp;errno_t err = fopen_s(&fp, "C:\\Users\\86173\\Desktop\\Data1.txt", "r");//注意：Data.txt的属性中显示的是C:\Users\86173\Desktop//需要将单斜杠变双斜杠，双斜杠变四斜杠if (fp == NULL){cout << "文件读取错误！";return -1;}for (int i = 0; i < txtRows; i++){for (int j = 0; j < txtCols; j++){fscanf_s(fp, "%d", &A[i][j]);/*每次读取一个数，fscanf_s函数遇到空格或者换行结束*/}fscanf_s(fp, "\n");}fclose(fp);AGraph* G;CreatAdj(G, A, 8);cout << "邻接表形式：" << endl;DisAdj(G);cout << endl<<"邻接表的深度遍历序列为：";DFSA(G, 2);return 0;
}

3. 结果

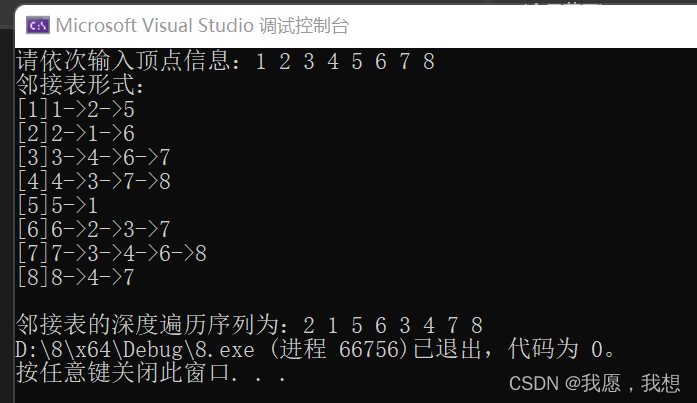
4. Data1.txt数据

0 1 0 0 1 0 0 0
1 0 0 0 0 1 0 0
0 0 0 1 0 1 1 0
0 0 1 0 0 0 1 1
1 0 0 0 0 0 0 0
0 1 1 0 0 0 1 0
0 0 1 1 0 1 0 1
0 0 0 1 0 0 1 0

三、广度优先搜索

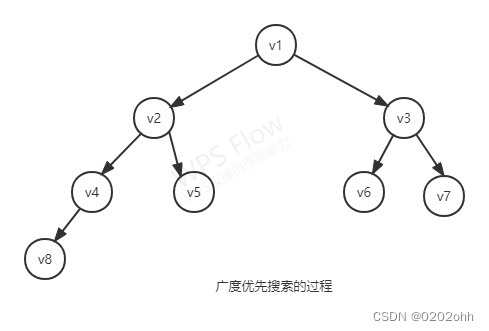
广度优先搜索（Breadth - First Search）是指照广度方向搜索，它类似于树的层次遍历，是树的按层次遍历的推广。
广度优先搜索的基本思想是：

访问顶点v
依次访问顶点v的各个未被访问的邻接点
分别从这些邻接点出发，依次访问它们的邻接点，并使“先被访问的顶点的邻接点”先于”后被访问的顶点的邻接点”被访问
若此时图中尚有顶点未被访问，则任选其一为起点，重复，直至图中所有顶点都被访问到

（一）基于邻接矩阵的广度优先遍历

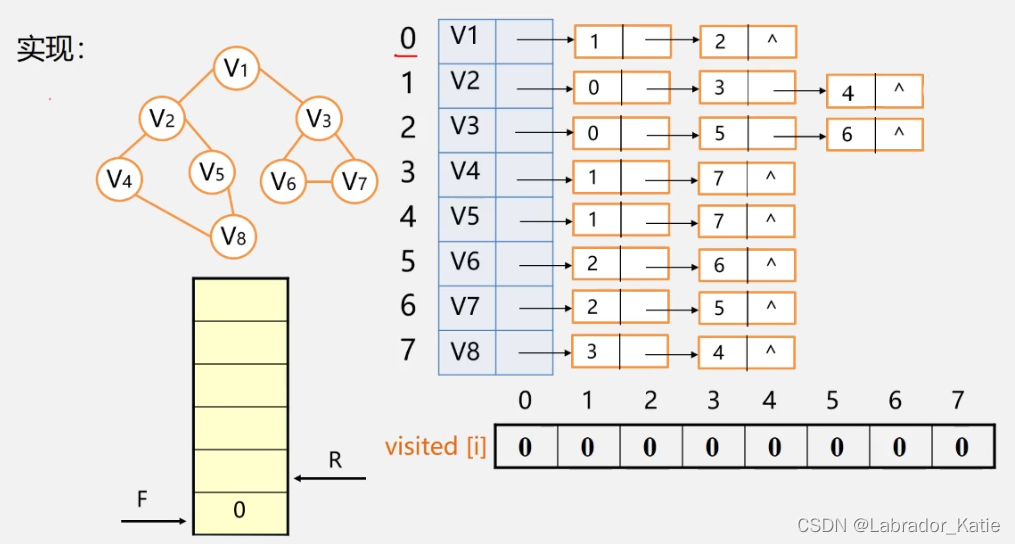
1. 演示

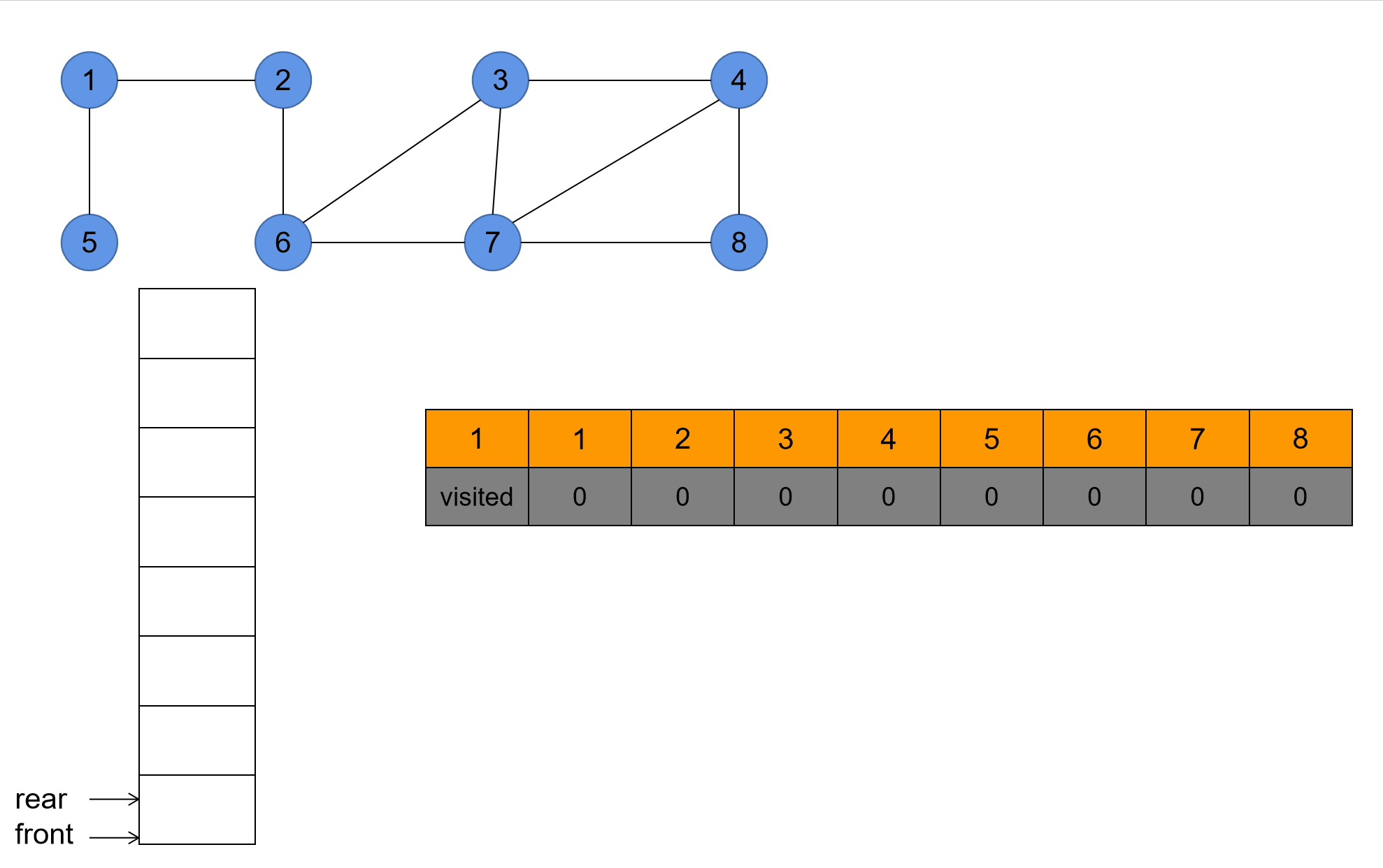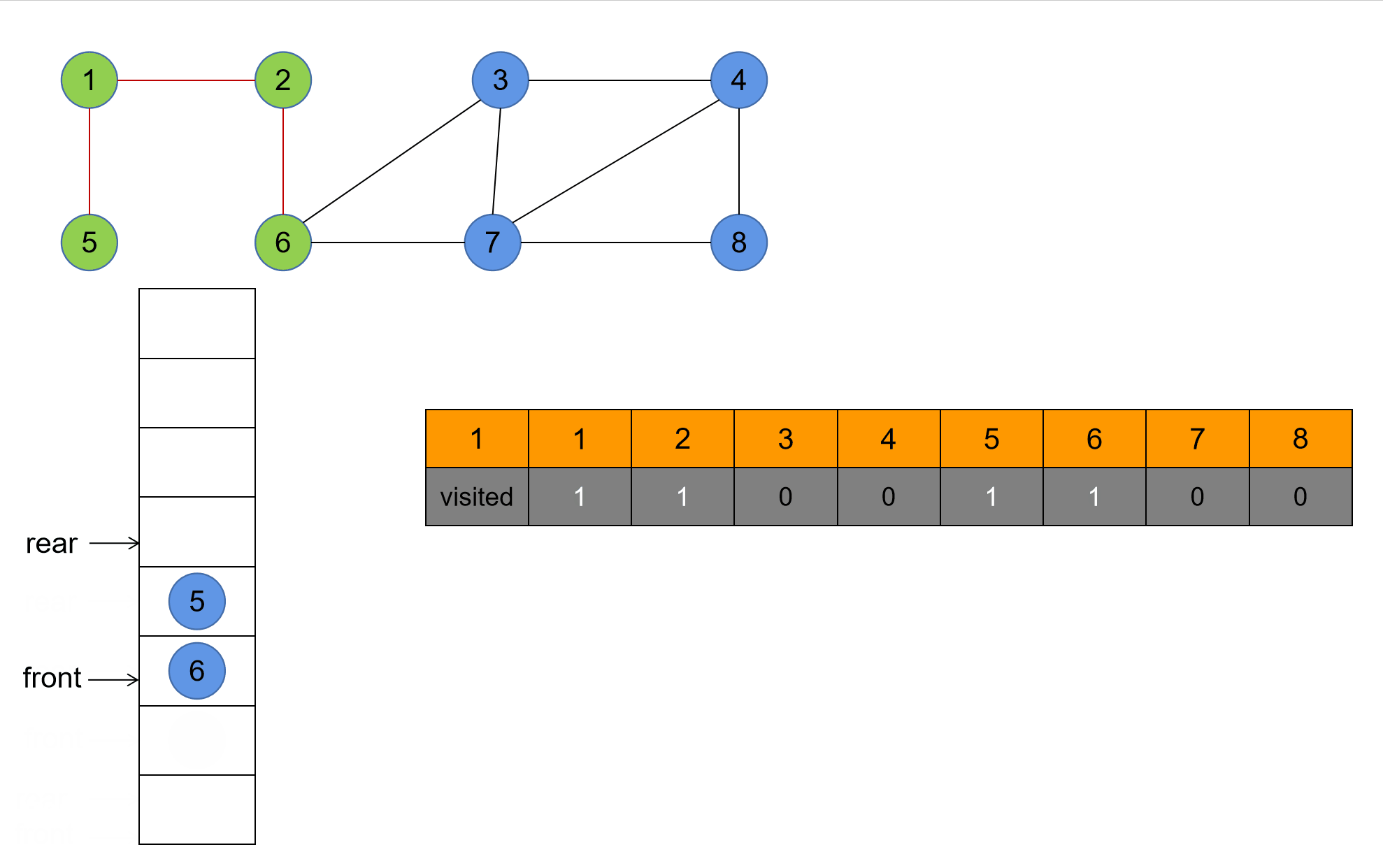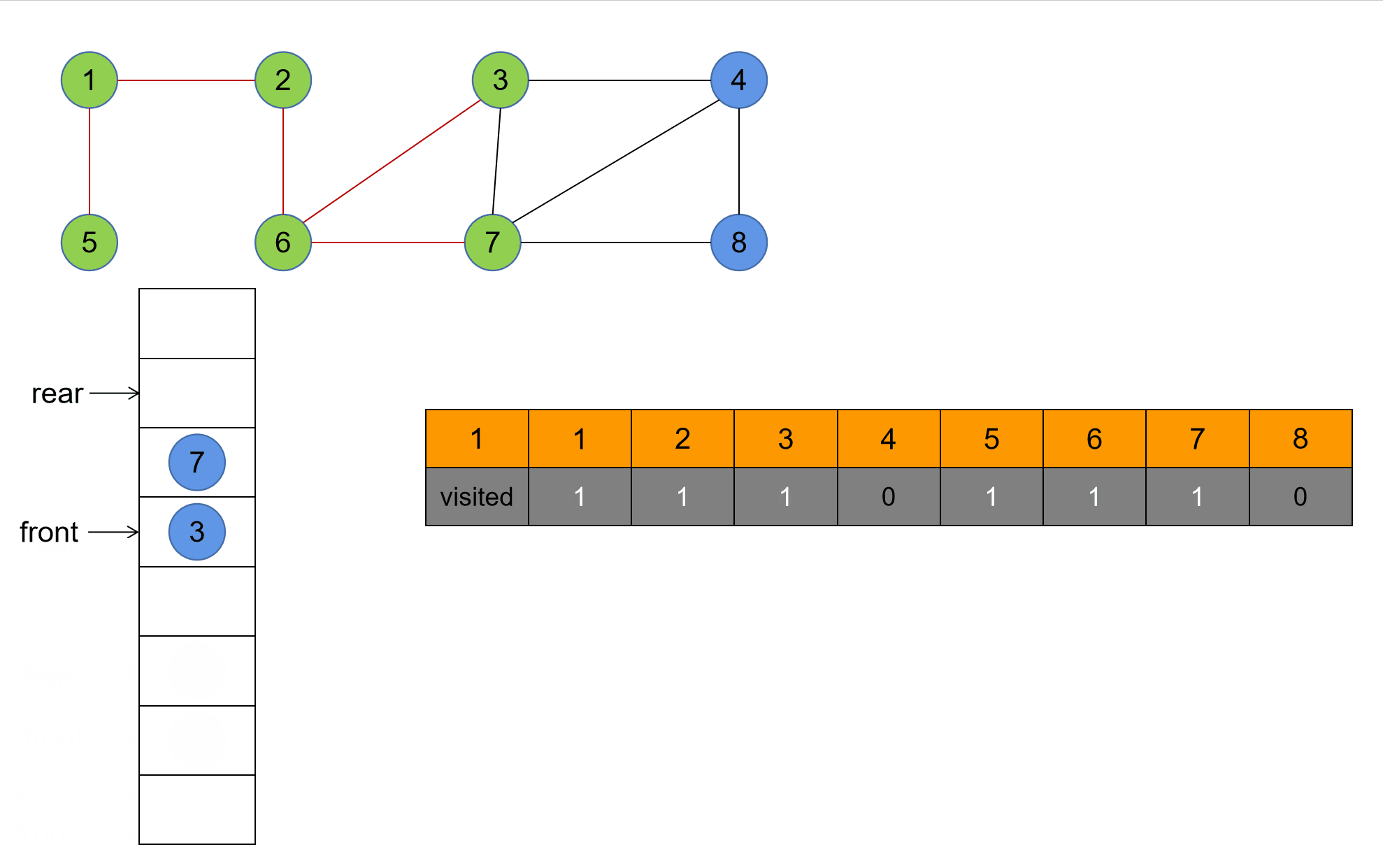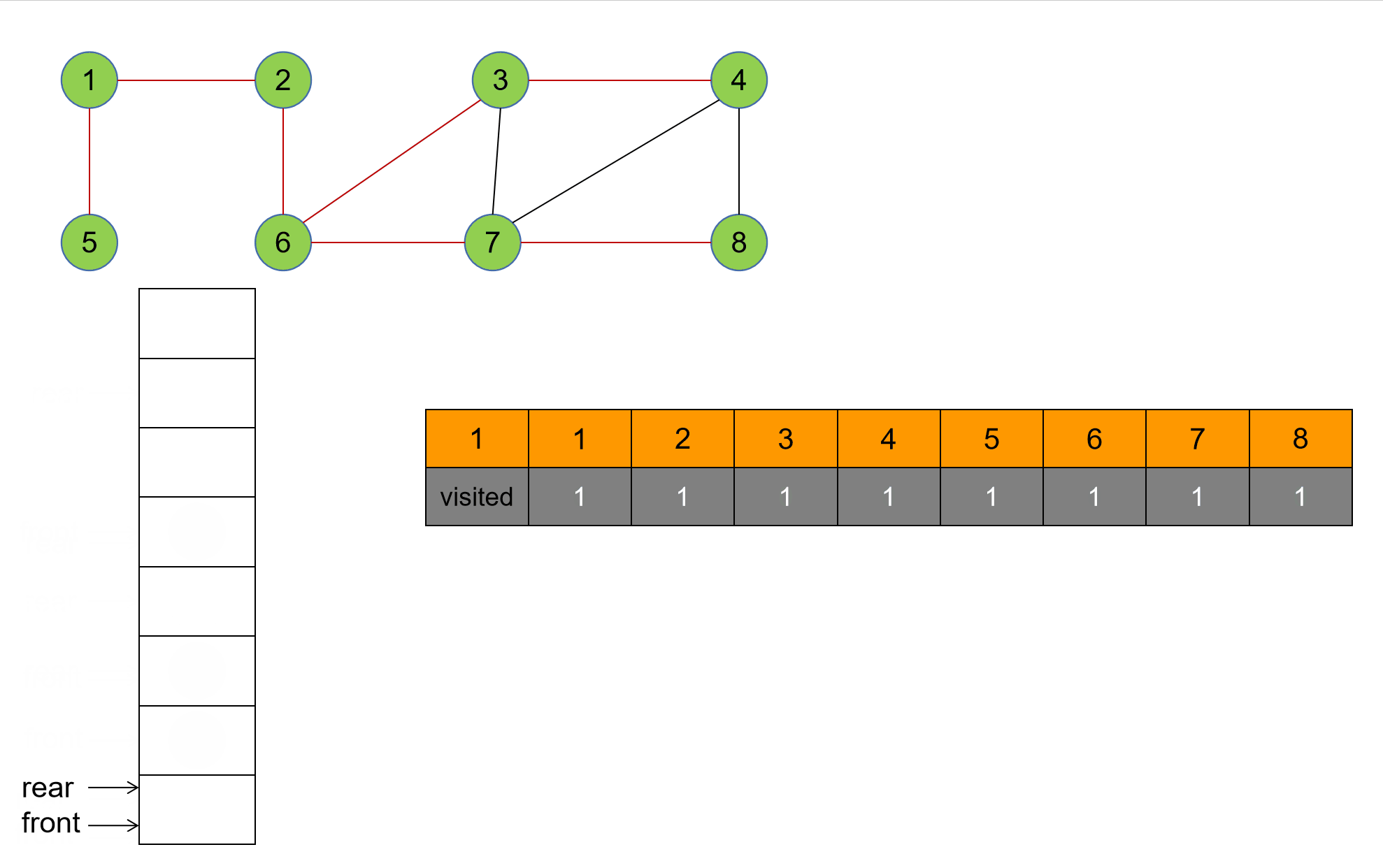
2. 核心代码

void BFS(MGraph* G, int v)//从v出发，广度优先遍历图G
{visit(v);//访问vvisited[v] = true;//对v做已访问的标记EnQueue(Q, v);//顶点v入队列Qwhile (!isEmpty(Q)){DeQueue(Q, v);//顶点v出队列for (int w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w)){if (!visited[w]){visit(w);//访问顶点wvisited[w] = true;EnQueue(Q, w);//顶点w出队}}}
}

3. 完整代码

MGraph.h

#pragma once
#include<iostream>
#include<stdbool.h>
using namespace std;#include<string>
#include<io.h>
#include<fstream>
#define txtRows 8 //行数
#define txtCols 8  //列数#define MAXSIZE 10
#define MaxVertexNum 100//顶点数目的最大值
//#define INFINITY  100000//宏定义常量“无穷”
#define MAXV 100
typedef int VertexType;//顶点的数据类型
typedef int EdgeType;//带权图中边上权值的数据类型
typedef struct
{VertexType vexs[MaxVertexNum];//顶点表（存放顶点）EdgeType edges[MaxVertexNum][MaxVertexNum];//邻接矩阵,边表（存放任意两个顶点之间的距离）int n, e;//图的当前顶点数和边数/弧数
}MGraph;void CreatMat(MGraph& G, int A[][MAXV], int n);//由数组A[n][n]生成邻接矩阵G
void DisMGraph(MGraph& G);//遍历打印
int FirstNeighbor(MGraph G, int x);//求图G中第x个顶点的第一个邻接点，若有则返回顶点号；
//若没有邻接点或图中不存在x，则返回-1
int NextNeighbor(MGraph G, int x, int y);//假设图G中第y个顶点是第x个顶点的一个邻接点，
//返回除第y个顶点之外，第x个顶点的下一个邻接点的顶点号；若第y个顶点是第x个顶点的最后一个邻接点，则返回-1//void BFS(MGraph G, int v);//从顶点v出发，广度优先遍历
void BFS(MGraph G, int i);//从第i个顶点出发，广度优先遍历

MGraph1.cpp


#include"AGraph.h"void CreatMat(MGraph& G, int A[][MAXV], int n)//由数组A[n][n]生成邻接矩阵G
{G.n = n;G.e = 0;cout << "请依次输入顶点信息：";for (int i = 1; i <= G.n; i++){cin >> G.vexs[i];}for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){G.edges[i + 1][j + 1] = A[i][j];//i+1，j+1是为了从为了从二维数组[1][1]开始存储if (A[i][j] != 0 && A[i][j] != INFINITY){G.e++;//边数加1}}}
}void DisMGraph(MGraph& G)//遍历打印
{for (int i = 1; i <= G.n; i++){for (int j = 1; j <= G.n; j++){cout << G.edges[i][j] << " ";}cout << endl;}
}int visited[MAXV] = { 0 };int FirstNeighbor(MGraph G, int x)//求图G中第x个顶点的第一个邻接点，若有则返回顶点号；
//若没有邻接点或图中不存在x，则返回-1
{for (int j = 1; j <= G.n; j++){if (G.edges[x][j] == 1)//寻找第x个顶点的第一个邻接点{return j;//返回第x个顶点的第一个邻接点的顶点号}}return -1;
}
int NextNeighbor(MGraph G, int x, int y)//假设图G中第y个顶点是第x个顶点的一个邻接点，
//返回除第y个顶点之外，第x个顶点的下一个邻接点的顶点号；若第y个顶点是第x个顶点的最后一个邻接点，则返回-1
{int i = 1, j = 1;for (int k = y + 1; k <= G.n; k++)//在邻接矩阵第x个顶点所在行//从第y个顶点之后寻找与第x个顶点邻接的顶点{if (G.edges[x][k] == 1){return k;}}return -1;
}void BFS(MGraph G, int i)//从第i个顶点出发，广度优先遍历
{VertexType Qu[MAXV];//定义循环队列int front = 0, rear = 0;//初始化cout << G.vexs[i] << " ";//访问第i个顶点visited[i] = 1;//第i个顶点标记为已访问Qu[rear] = G.vexs[i];//第i个顶点入队rear = (rear + 1) % MAXSIZE;while (front != rear){VertexType w = Qu[front];front = (front + 1) % MAXSIZE;int m=0;for (int k=1; k <= G.n; k++){if (G.vexs[k] == w){m = k;break;}}for (int w = FirstNeighbor(G, m); w > 0; w = NextNeighbor(G, m, w)){if (!visited[w])//第w个顶点为第v个顶点尚且未访问的顶点{cout << G.vexs[w] << " ";visited[w] = 1;Qu[rear] = G.vexs[w];//第w个顶点入队rear = (rear + 1) % MAXSIZE;}}}
}

Text.cpp

#include"AGraph.h"
int main()
{int A[MAXV][MAXV];FILE* fp;errno_t err = fopen_s(&fp,"C:\\Users\\86173\\Desktop\\Data1.txt","r");if (fp == NULL){return -1;}for (int i = 0; i < txtRows; i++){for (int j = 0; j < txtCols; j++){fscanf_s(fp,"%d", & A[i][j]);}fscanf_s(fp, "\n");}fclose(fp);MGraph G;CreatMat(G, A, 8);cout << "邻接矩阵形式：" << endl;DisMGraph(G);cout << "从第2个顶点出发广度优先遍历顺序为：" << endl;BFS(G, 2);return 0;}

4. 结果

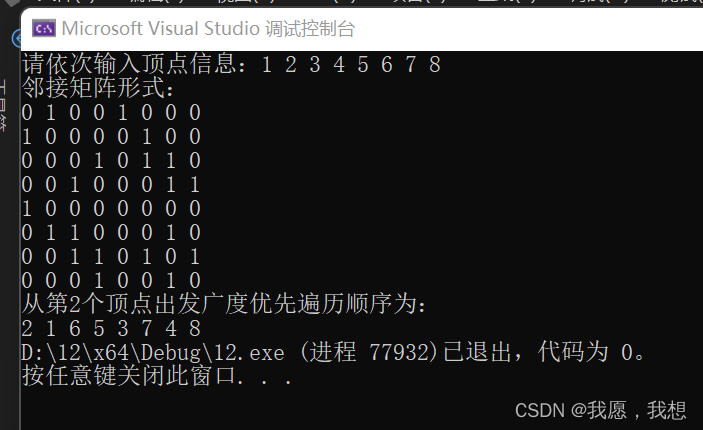
（二）基于邻接表的广度优先遍历

1. 核心代码

void BFS(AGraph* G, int v);//从顶点v出发，广度优先遍历
void BFS2(AGraph* G, int i);//从第i个顶点出发，广度优先遍历int visited[MAXV] = { 0 };
void BFS(AGraph* G, int v)//从顶点v出发，广度优先遍历
{ArcNode* p = NULL;int Qu[MAXV];int front = 0, rear = 0;int w;cout << v << " ";visited[v] = 1;Qu[rear] = v;rear = (rear + 1) % MAXSIZE;while (front != rear){w = Qu[front];front = (front + 1) % MAXSIZE;p = G->adjlist[w].firstarc;while (p != NULL){if (visited[p->adjvex] == 0){cout << p->adjvex << " ";visited[p->adjvex] = 1;Qu[rear] = p->adjvex;rear = (rear + 1) % MAXSIZE;}p = p->nextarc;}}
}
void BFS2(AGraph* G, int i)//从第i个顶点出发，广度优先遍历
{ArcNode* p;ElemType Qu[MAXV];//定义循环队列int front = 0, rear = 0;//初始化cout << G->adjlist[i].data << " ";//访问第i个顶点visited[i] = 1;//第i个顶点标记为已访问Qu[rear] = G->adjlist[i].data;//第i个顶点入队rear = (rear + 1) % MAXSIZE;while (front != rear){ElemType w = Qu[front];front = (front + 1) % MAXSIZE;int m=0;for (int k=1; k <= G->n; k++){if (G->adjlist[k].data == w){m = k;break;}}p = G->adjlist[m].firstarc;while (p != NULL){if (visited[p->adjvex] == 0){cout << G->adjlist[p->adjvex].data << " ";visited[p->adjvex] = 1;Qu[rear] = G->adjlist[p->adjvex].data;rear = (rear + 1) % MAXSIZE;}p = p->nextarc;}}
}

2. 完整代码

AGraph.h

#pragma once
#include<iostream>
#include<stdbool.h>
using namespace std;#include<string>
#include<io.h>
#include<fstream>
#define txtRows 8 //行数
#define txtCols 8  //列数#define MAXV 100//最多顶点个数
#define INF 10000//“无穷”
#define MAXSIZE 6
typedef int ElemType;
typedef int InfoType;
typedef struct ANode//边结点类型
{int adjvex;InfoType info;struct ANode* nextarc;
}ArcNode;typedef struct Vode//表头结点类型
{ElemType data;//顶点信息ArcNode* firstarc;
}VNode;typedef VNode Adjlist[MAXV];//Adjlist是邻接表类型typedef struct
{int n, e;Adjlist adjlist;
}AGraph;void CreatAdj(AGraph*& G, int A[][MAXV], int n);//创建邻接表
void DisAdj(AGraph* G);//打印void BFS(AGraph* G, int v);//从顶点v出发，广度优先遍历
void BFS2(AGraph* G, int i);//从第i个顶点出发，广度优先遍历

AGraph1.cpp

#include"AGraph.h"
void CreatAdj(AGraph*& G, int A[][MAXV], int n)
{G = (AGraph*)malloc(sizeof(AGraph));G->n = n;G->e = 0;cout << "请依次输入各顶点：" << endl;for (int i = 1; i <= G->n; i++){cin >> G->adjlist[i].data;G->adjlist[i].firstarc = NULL;}for (int i = 0; i < G->n; i++){for (int j = (G->n)-1; j >=0; j--){if (A[i][j] != 0 && A[i][j] != INF){ArcNode* p = (ArcNode*)malloc(sizeof(ArcNode));p->info = A[i][j];p->adjvex = j + 1;p->nextarc = G->adjlist[i + 1].firstarc;//头插G->adjlist[i + 1].firstarc = p;G->e++;}}}
}void DisAdj(AGraph* G)//打印
{ArcNode* p;for (int i = 1; i <= G->n; i++){cout << "[" << i << "]" << G->adjlist[i].data;p = G->adjlist[i].firstarc;//p为第i个顶点的第一个邻接点while (p != NULL){cout << "->";cout << p->adjvex;p = p->nextarc;}cout << endl;}
}int visited[MAXV] = { 0 };
void BFS(AGraph* G, int v)//从顶点v出发，广度优先遍历
{ArcNode* p = NULL;int Qu[MAXV];int front = 0, rear = 0;int w;cout << v << " ";visited[v] = 1;Qu[rear] = v;rear = (rear + 1) % MAXSIZE;while (front != rear){w = Qu[front];front = (front + 1) % MAXSIZE;p = G->adjlist[w].firstarc;while (p != NULL){if (visited[p->adjvex] == 0){cout << p->adjvex << " ";visited[p->adjvex] = 1;Qu[rear] = p->adjvex;rear = (rear + 1) % MAXSIZE;}p = p->nextarc;}}
}
void BFS2(AGraph* G, int i)//从第i个顶点出发，广度优先遍历
{ArcNode* p;ElemType Qu[MAXV];//定义循环队列int front = 0, rear = 0;//初始化cout << G->adjlist[i].data << " ";//访问第i个顶点visited[i] = 1;//第i个顶点标记为已访问Qu[rear] = G->adjlist[i].data;//第i个顶点入队rear = (rear + 1) % MAXSIZE;while (front != rear){ElemType w = Qu[front];front = (front + 1) % MAXSIZE;int m=0;for (int k=1; k <= G->n; k++){if (G->adjlist[k].data == w){m = k;break;}}p = G->adjlist[m].firstarc;while (p != NULL){if (visited[p->adjvex] == 0){cout << G->adjlist[p->adjvex].data << " ";visited[p->adjvex] = 1;Qu[rear] = G->adjlist[p->adjvex].data;rear = (rear + 1) % MAXSIZE;}p = p->nextarc;}}
}

Text.cpp

#include"AGraph.h"
int main()
{int A[MAXV][MAXV];FILE* fp;errno_t err = fopen_s(&fp,"C:\\Users\\86173\\Desktop\\Data1.txt","r");if (fp == NULL){return -1;}for (int i = 0; i < txtRows; i++){for (int j = 0; j < txtCols; j++){fscanf_s(fp,"%d", & A[i][j]);}fscanf_s(fp, "\n");}fclose(fp);AGraph *G;CreatAdj(G, A, 8);DisAdj(G);cout << "从第2个顶点出发广度优先遍历顺序为：" << endl;BFS2(G, 2);return 0;}