一个图形G=(V,E)，存在某一顶点v，希望从v开始，通过此顶点相邻的顶点而去访问G中其他顶点直达全部的顶点遍历完毕。在遍历的过程中可能会重复经过某些顶点及边线，经由图形的遍历可以判断该图形是否连通，并找出连通单元和路径。
图形遍历有两种方法：

• 深度优先搜索Deep-First-Search
• 广度优先搜索Breadth-First-Search

一、深度优先搜索

从图形的某一顶点开始遍历，被访问过的顶点做上已访问的标记，接着从与此顶点相邻且未访问过的顶点中选择任意一个顶点，并做上已访问的记号，再以该顶点为新的起点进行深度优先搜索遍历。

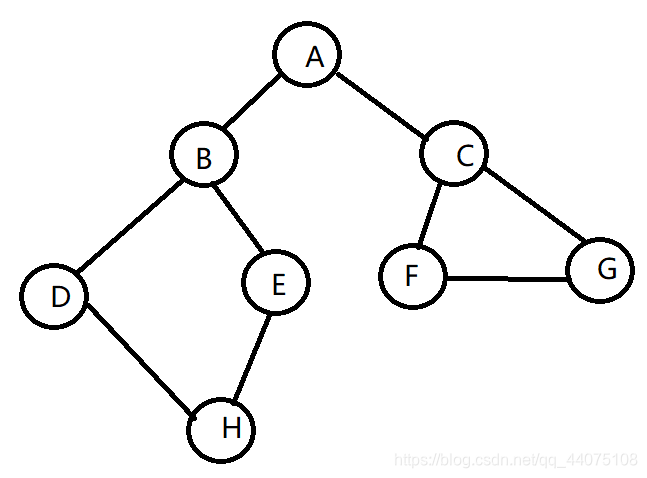
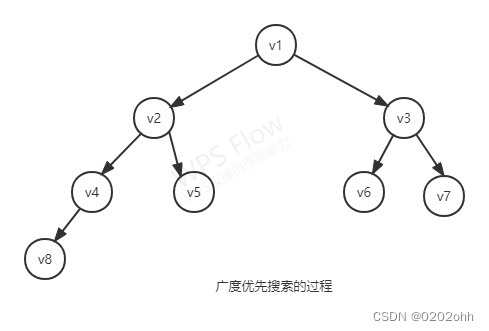
我们以下图为例进行代码实现：

定义public static void DFS(int current)实现深度优先搜索，定义数组run[]来标记顶点的遍历情况，1表示已遍历，0表示未遍历。图使用邻接表进行存放，从选定顶点的链表的头结点进行判断，若该顶点未遍历，则递归调用该函数从该节点开始进行深度优先遍历，否则指针后移寻找该顶点未被遍历的顶点。

public static void DFS(int current)代码如下：

    public static void DFS(int current) {run[current]=1;                                        //改顶点设为已遍历System.out.print("["+current+"]");                     //打印顶点while(head[current].first!=null) {                     //从链表头结点开始if(run[head[current].first.data]==0)               //若该顶点未遍历就进行DFS递归调用DFS(head[current].first.data);head[current].first=head[current].first.next;      //否则指针后移}}

主要代码如下：（Node类和GraphLink类的定义见博客图表示法中的邻接表法
http://blog.csdn.net/zd454909951/article/details/78896793）

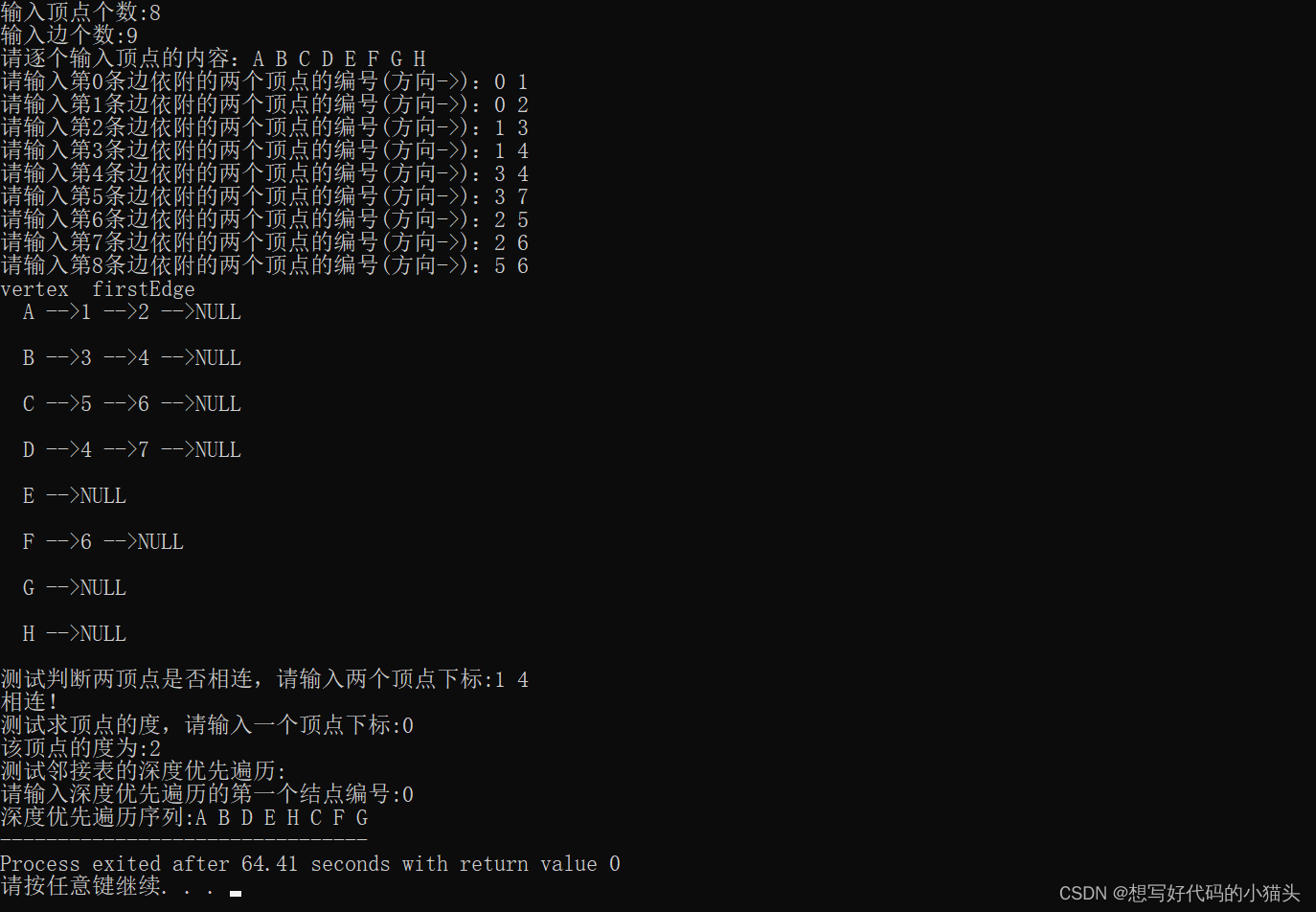
public class Test {//静态变量可全局使用public static int[] run=new int[9];                     //判断顶点是否已遍历，1代表遍历，0代表未遍历public static GraphLink[] head=new GraphLink[9];        //声明链接表数组public static void main(String[] args) {int data[][]= {{1,2},{2,1},{1,3},{3,1},{2,4},{4,2},{2,5},{5,2},{3,6},{6,3},{3,7},{7,3},{4,5},{5,4},{6,7},{7,6},{5,8},{8,5},{6,8},{8,6}};System.out.println("图形的邻接表的内容：");for(int i=1;i<9;i++) {run[i]=0;head[i]=new GraphLink();System.out.print("顶点"+i+"=>");for(int j=0;j<data.length;j++) {if(data[j][0]==i)head[i].insert(data[j][1]);}head[i].print();}System.out.println("深度优先遍历顶点：");DFS(1);    //从顶点1开始遍历System.out.println();}

程序运行结果如下：

递归函数DFS具体运行过程如下：

二、广度优先搜索

从图中的某一顶点开始遍历，然后访问所有与其相邻的顶点，最后访问所有与这些顶点相邻的顶点。
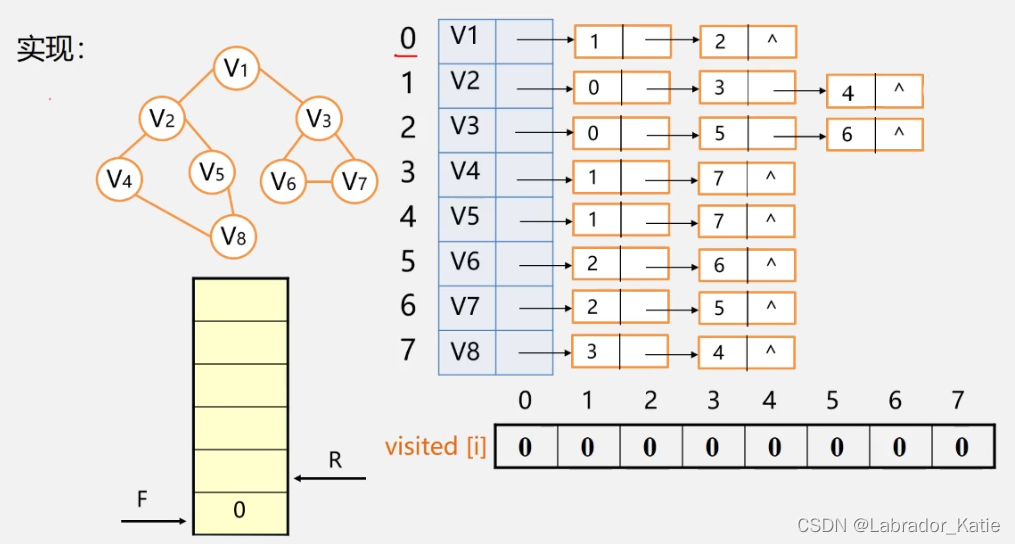
代码中需要用到队列，选择一个顶点入队，然后将其所有相邻的未被访问的顶点都入队，依次对队列中的顶点进行上述操作直到队列为空。

public static void BFS(int current)代码如下：

    /*广度优先搜索函数*/public static void BFS(int current) {Node tempNode;enqueue(current);                                         //将第一个顶点存入队列run[current]=1;                                           //将遍历过的顶点设为1System.out.print("["+current+"]");                        //打印该遍历过的顶点while(front!=rear) {                                      //判断队列是否为空current=dequeue();                                    //从队列中取出顶点tempNode=head[current].first;                         //记录目前顶点的链表的表头while(tempNode!=null) {                               //判断该顶点的链表是否为空，即遍历所有与该顶点相邻的顶点if(run[tempNode.data]==0) {                       //相邻的顶点未遍历enqueue(tempNode.data);                       //访问该顶点并存入队列run[tempNode.data]=1;                         //将该顶点标记为已遍历System.out.print("["+tempNode.data+"]");      //打印该顶点}tempNode=tempNode.next;                           //指针后移，继续遍历出队列顶点的链表}}}/*入队*/public static void enqueue(int value) {if(rear>=MAXSIZE)                                         //队列已满return;rear++;queue[rear]=value;}/*出队*/public static int dequeue() {if(front==rear)                                           //队列为空return -1;front++;return queue[front];}

主要代码如下：（Node类和GraphLink类的定义见博客图表示法中的邻接表法
http://blog.csdn.net/zd454909951/article/details/78896793）

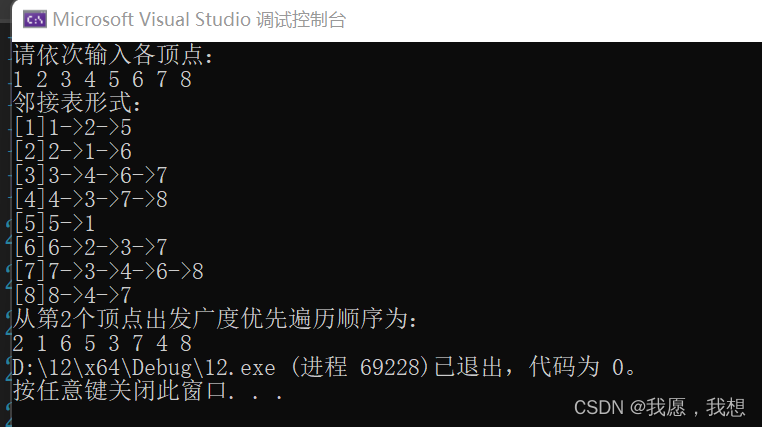
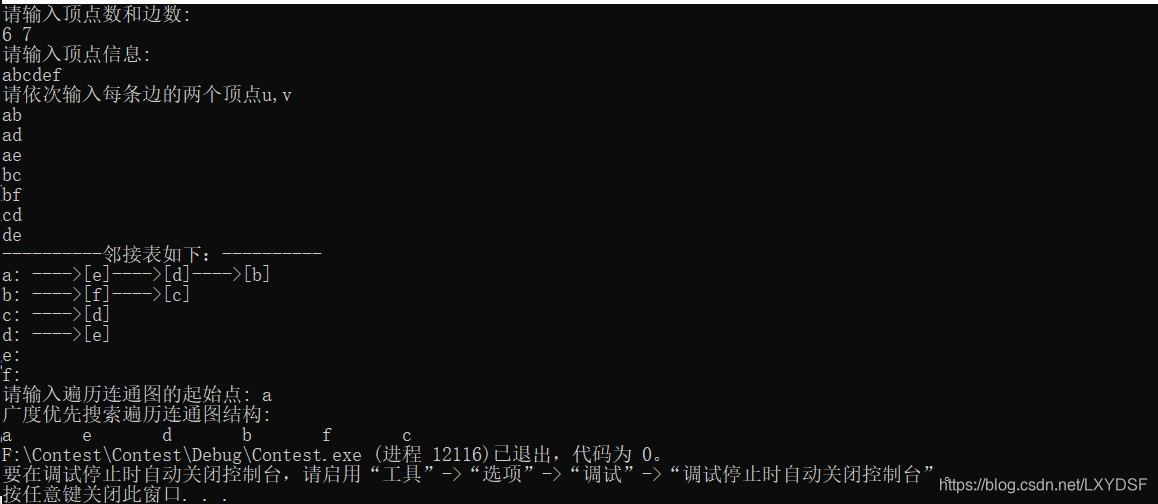
public class Test {public static int[] run=new int[9];                          //用来记录各顶点是否遍历过public static GraphLink[] head=new GraphLink[9];public final static int MAXSIZE=10;                          //定义队列的最大容量static int[] queue=new int[MAXSIZE];                         //队列数组的声明static int front=-1,rear=-1;                                 //定义队列的头指针和尾指针public static void main(String[] args) {int data[][]= {{1,2},{2,1},{1,3},{3,1},{2,4},{4,2},{2,5},{5,2},{3,6},{6,3},{3,7},{7,3},{4,5},{5,4},{6,7},{7,6},{5,8},{8,5},{6,8},{8,6}};System.out.println("图形的邻接表的内容：");for(int i=1;i<9;i++) {run[i]=0;head[i]=new GraphLink();System.out.print("顶点"+i+"=>");for(int j=0;j<data.length;j++) {if(data[j][0]==i)head[i].insert(data[j][1]);}head[i].print();}System.out.println("深度优先遍历顶点：");BFS(1);  //调用广度优先搜索函数，从顶点1开始访问System.out.println();}
}

程序运行结果如下：