微信8.0版本开始微信好友的最大数量，将之前的最多5000好友提升到现在的10000好友。

不要相信那些一天加500人1000人的，不可能的！腾讯对这方面是有严格限制的。

但是会区分你的微信号质量，质量越好加人越有利。以下内容是增对普通帐号。刚注册的新号和优质帐号不在以下讨论范围内。

一、通过电话通讯录主动添加

每天不超过25人，超过会提示操作频繁，或者即使你发出去了，对方也收不到信息。这个对微信新号尤其严格。新号就是注册15天以内的帐号。

二、通过扫一扫主动添加

每天不超过20-25人，超过一样会有提示。

三、通过微信群聊主动添加（用的最多）

每日不超过50人，超过没有提示，你发送出去对方也是收不到信息的。并且会受到群聊质量的影响，群质量很差，群成员的质量很差，也会影响家人数量

四、手机号主动搜索添加

每天不超过30人，这个是长期实践得出的结果。尤其是教育、保险等行业，经常通过手机搜索加好友，一定不要急。心急吃不了热豆腐，必须慢慢来。如果非常着急，可以尝试多个wx号同时添加。确保每个手机号一天30人左右。

五、被动添加

被动添加，也就是别人通过二维码、名片或手机号搜索添加你的。这种情况也是有严格限制的。

每天通过好友数量不要超过200人，原则上是不超过300人但只要达到或超过300人就会封号1-3天，申诉也没有用耐心等待，剩余添加好友未通过一般7天之后都会显示过期在添加就没有办法了。

六、微信自动加好友、群发

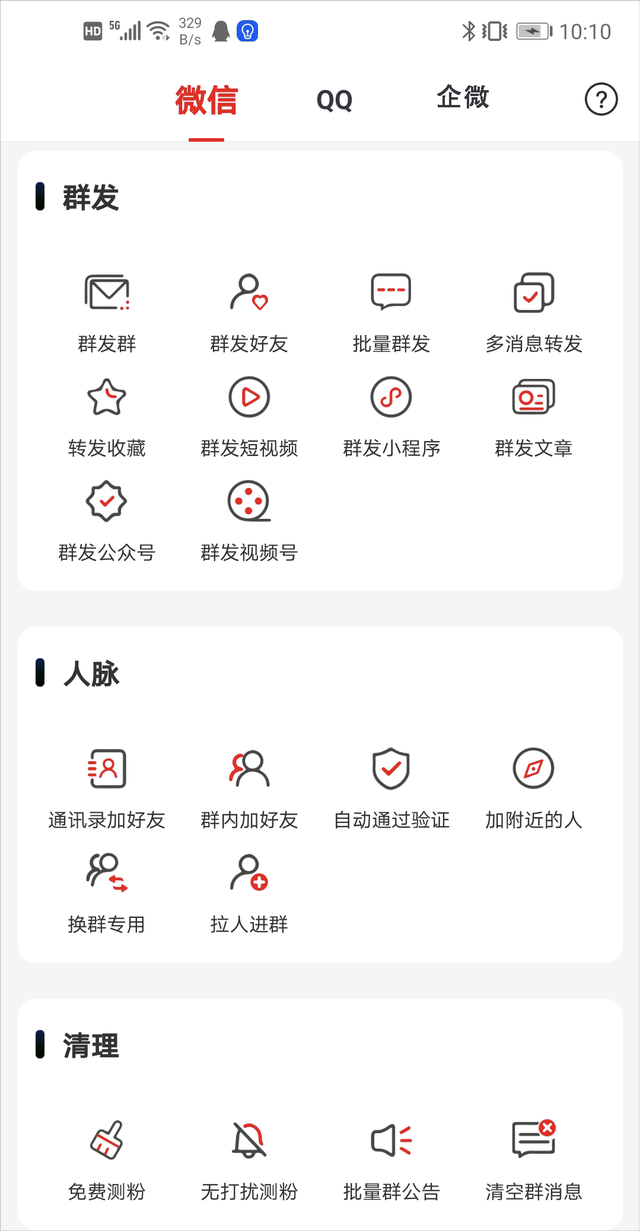
如果需要频繁群发、加好友，可以借助一些工具，每天加一定数量的好友，群内加、通讯录加、导入excel都可以，还能自动备注。比如“群发无忧”、“掌上无忧”等app。

给大家分享一个技巧，平常还可以借助这些工具的群发功能，给好友、群聊群发发消息。自动朋友圈点赞，刷刷存在感。可以大大节省时间。微信、短信、QQ都可以使用。

七、微信好友数量限制

首先虽然微信好友上限开放到了10000，但是建议一个微信号好友带到3500左右，就应该换微信号了。或者会增加微信号被判定为营销帐号的概率。

最后，目前微信好友的最大数量可能还不止10000，有可能已经达到了15000人之多。但是这个数据并没有得到微信官方团队的正式回应，而且目前暂时未发现这么多好友的用户。