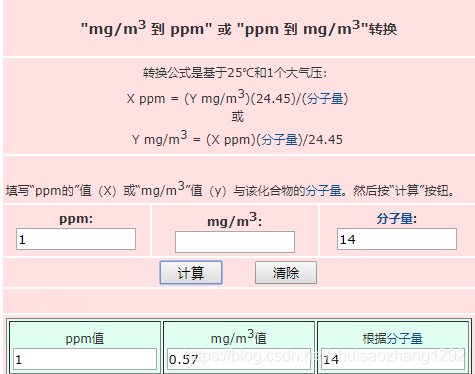
element el-table 加多选列
<el-table :data="tableData" height="500" style="width: 100%" center highlight-current-row ><el-table-column type="index" label="序号" width="50" align="center"> </el-table-column><el-table-column :resizable="false" :render-header="renderHeader" align="center"><template slot-scope="scope"><el-checkbox v-model="scope.row.itemCheck" @change="toggleCheck(scope.row)"></el-checkbox></template></el-table-column></el-table>
tableData: [{itemCheck: false,},{itemCheck: false,},{itemCheck: false,},],
isIndeterminate: false,
isCheck:false,
renderHeader(h, data) {return h("span", [h("el-checkbox", {on: {change: this.selectBox},props: {value: this.isCheck,indeterminate: this.isIndeterminate}},"授权")]);},selectBox() {this.isCheck = !this.isCheck;console.log(this.isCheck);let list = [...this.tableData];for (let val of list) {val.itemCheck = this.isCheck;}this.tableData = list;this.isIndeterminate = false;},toggleCheck(row) {// 获取已勾选let list = this.tableData.filter(item => item.itemCheck);this.isCheck = list.length === this.tableData.length//是否全选this.isIndeterminate = list.length > 0 && list.length < this.tableData.length;//是否半选},



![线性代数[矩阵的秩]](https://img-blog.csdnimg.cn/69b4b81ab286434aa888964314667510.jpeg)