目录

一、FTP的概述

1.1 FTP的理念

1.2 FTP数据连接模式

1.2.1 连接模式分类

1.2.2 主动和被动模式的工作原理

二、配置FTP服务

2.1 配置匿名用户FTP服务

2.1.1 关闭防火墙安装vsftpd软件包

2.1.2 开启FTP服务并做备份

​ 2.1.3 修改配置文件

2.1.4 设置目录下权限，便于用户上传数据

2.1.5 重启服务

2.1.6 win机器上匿名访问

​ 2.1.7 接收pub下的文件

 3.1 本地用户ftp访问

3.1.1 配置文件

3.1.2 设置用户登录时禁锢的根目录

3.1.3 设置用户的黑白名单

总结

---

一、FTP的概述

1.1 FTP的理念

●FTP（文件传输协议），是TCP/IP协议组中之一，经典的c/s构架的应用层协议。用于文件的双向传输。

●FTP协议包括：服务器和客户端。服务器是用来存储文件，用户可以通过客户端并用FTP协议去访问服务器上的文件资源。

●FTP协议默认协议是TCP协议，其端口号为20、21

20端口：用于建立数据连接并且传输文件数据

21端口：用于建立控制连接并传输FTP控制命令

1.2 FTP数据连接模式

1.2.1 连接模式分类

分为：主动模式 和 被动模式

①主动模式（standard）：服务器主动发起数据连接。

②被动模式（passive）：服务器被动的等待数据的连接

1.2.2 主动和被动模式的工作原理

①主动模式:

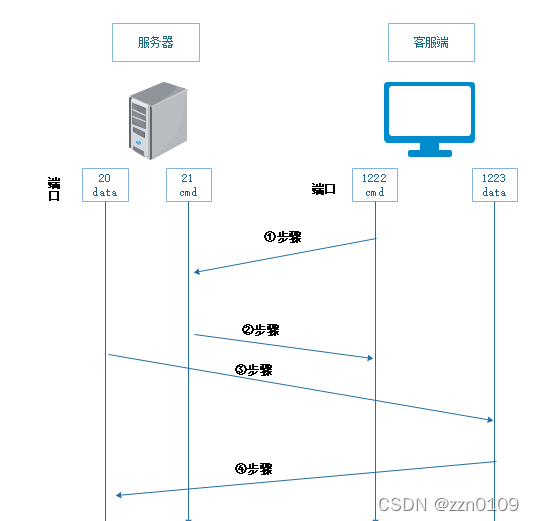
第一步：客户端向服务器发送FTP请求连接（用户、密码、命令端口等）

第二步：服务器收到请求后响应ACK确认包，服务器的21端口和客户端1222的高位端口进行连接

第三步：服务器20端口向客户端提供一个高位端口（1223）并发送连接请求

第四步：客户端向服务器发送ACK确认包并开始传输数据

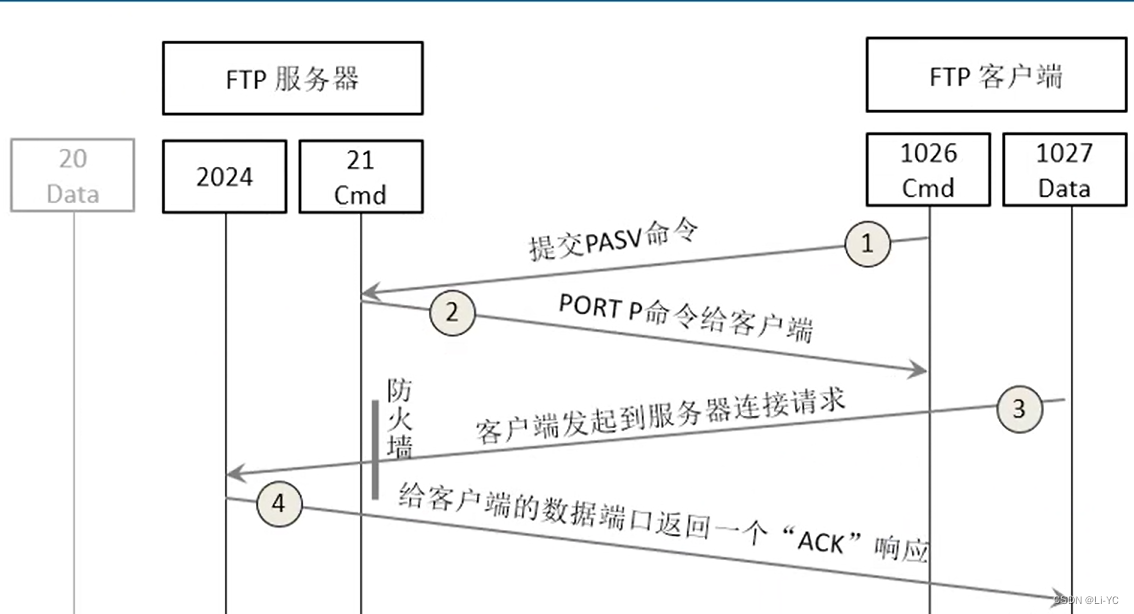
②被动模式：

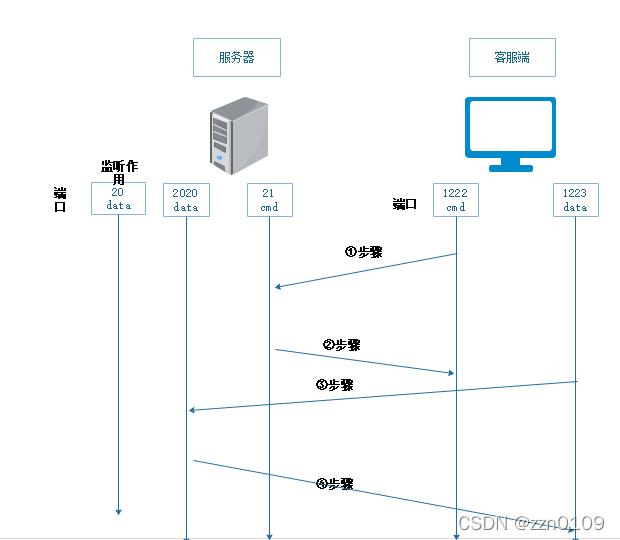
第一步：客户端向服务器发送个FTP连接请求和连接模式命令（PASV）

第二步：服务器响应ACK并开放一个1222高位端口告诉客户端等待客户端连接 21端口

第三步：客户端从自己的一个高位端口1223连接服务器响应的2020高位端口

第四步：服务器给客户端发送一个ACK响应并可以进行数据的传输

进行连接前要关闭防火墙

二、配置FTP服务

2.1 配置匿名用户FTP服务

2.1.1 关闭防火墙安装vsftpd软件包

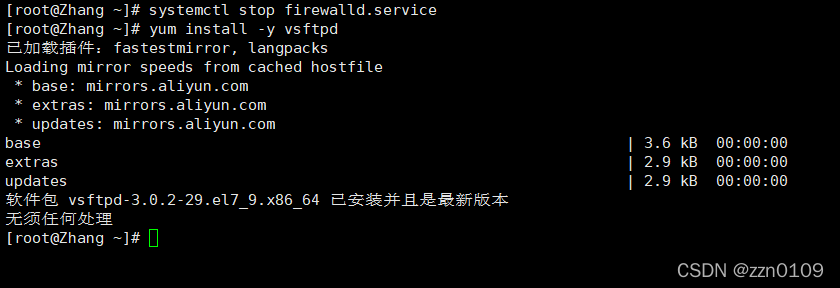
2.1.2 开启FTP服务并做备份

 2.1.3 修改配置文件

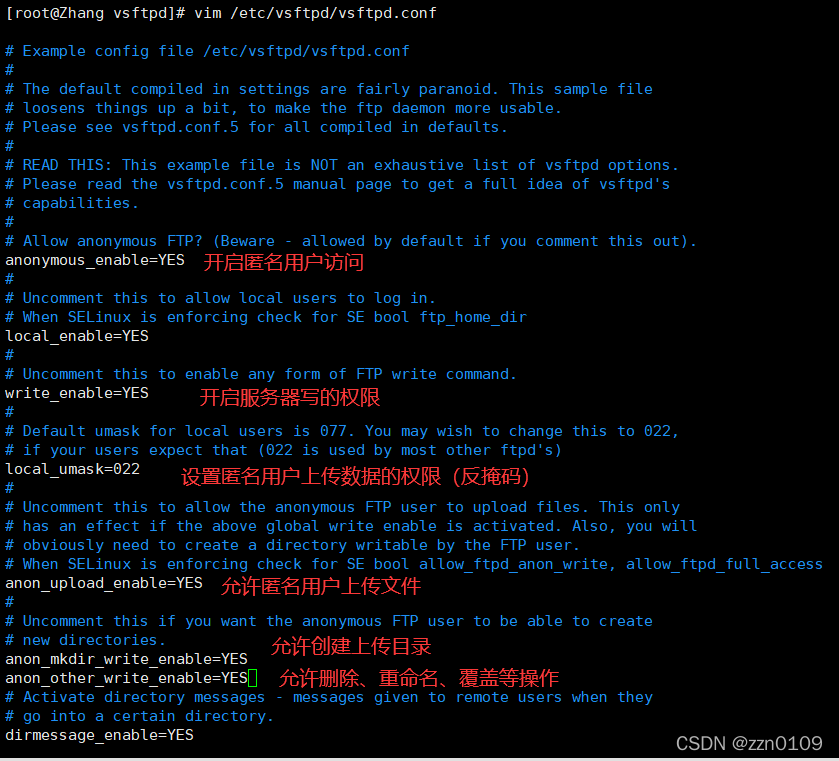
2.1.4 设置目录下权限，便于用户上传数据

 

2.1.5 重启服务

2.1.6 win机器上匿名访问

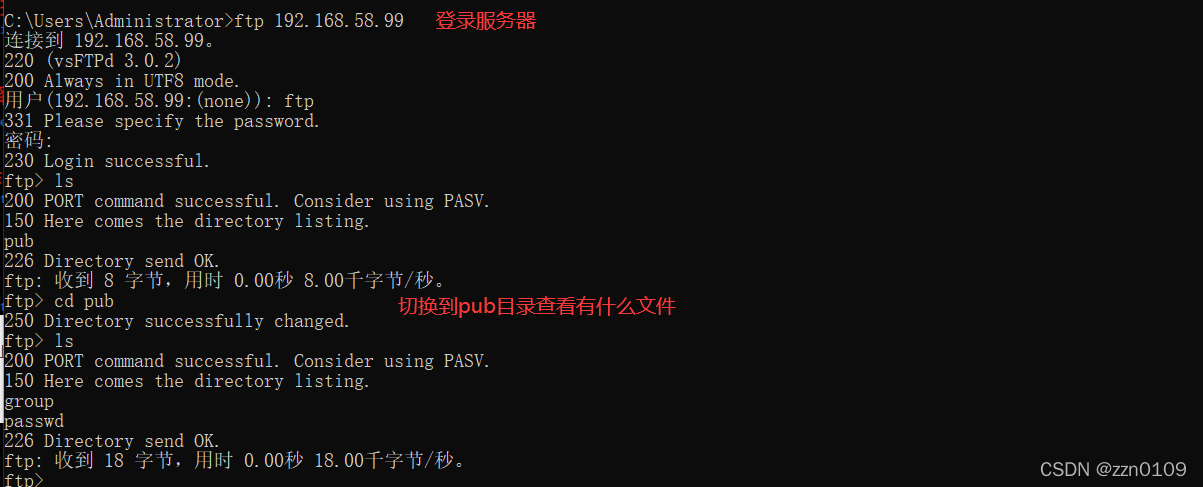 2.1.7 接收pub下的文件

 

 

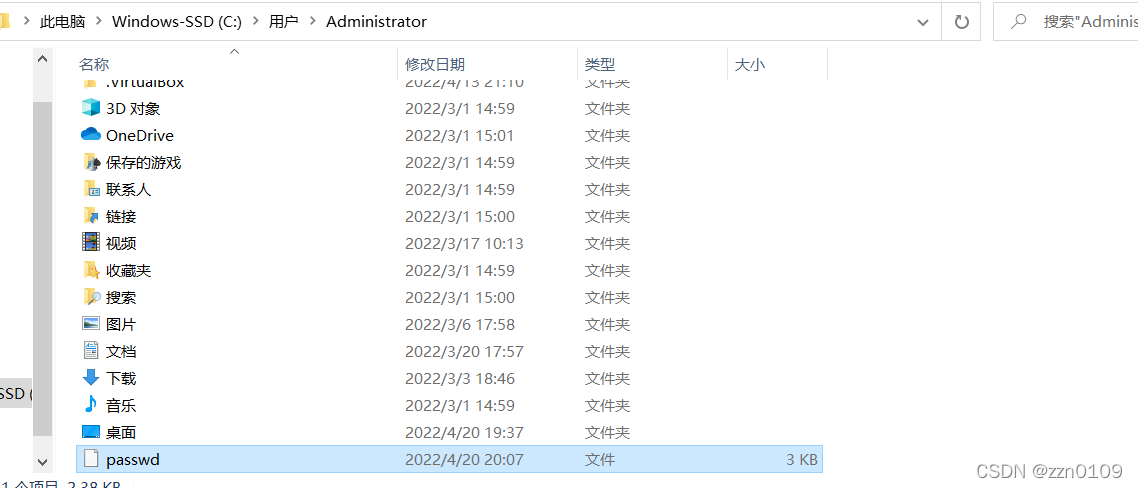
 3.1 本地用户ftp访问

3.1.1 配置文件

 

 

 

 

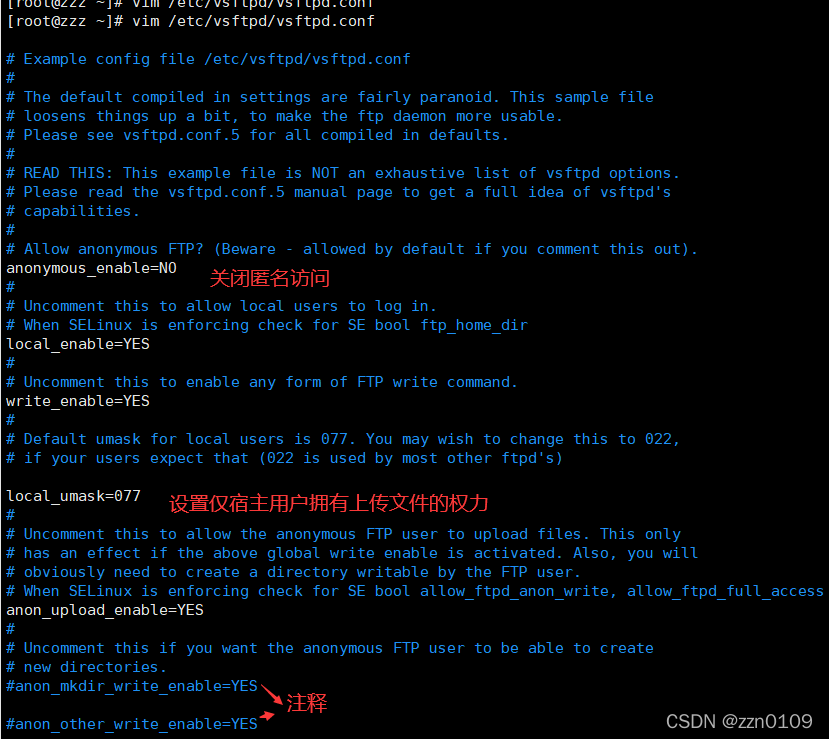
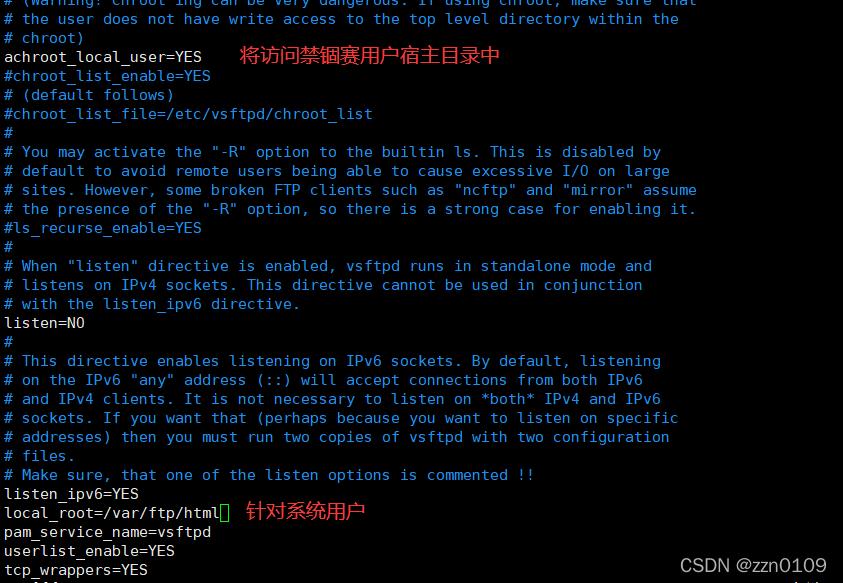
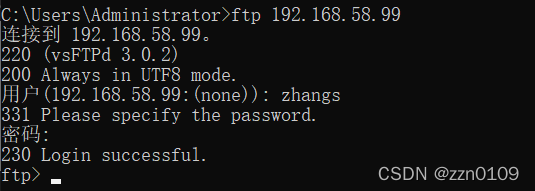
3.1.2 设置用户登录时禁锢的根目录

在vim /etc/vsftp/vsftp.conf

local_root=需要禁锢的目录    针对系统用户

anon_root=需要禁锢的目录    针对匿名用户

3.1.3 设置用户的黑白名单

vim /etc/vsftp/user_list

 

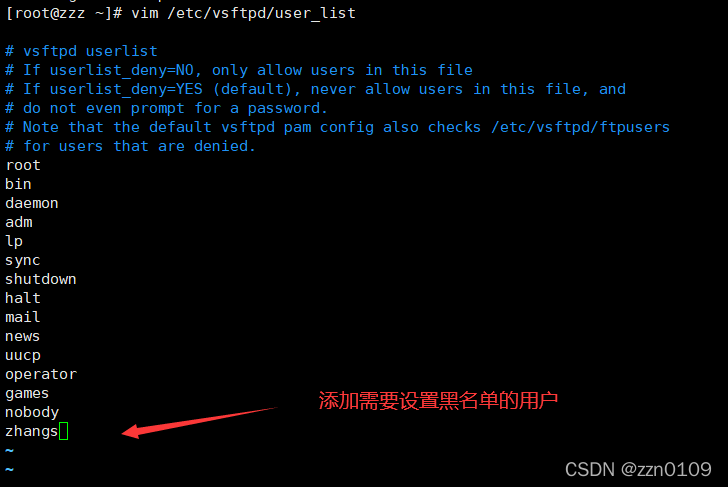
当userlist_deny=YES时

 

 

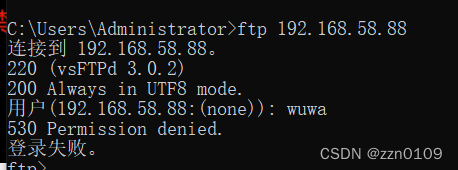
总结

FTP的简单概括

FTP连接的两种模式：主动和被动。  及其各自的工作原理

FTP连接的配置