目录
1、感受野
2、理论感受野计算
2.1、自上而下感受野计算
2.2、自下而上的计算方法
3、作用
4、关系
5、总结
6、参考文献
经典目标检测和最新目标跟踪都用到了RPN(region proposal network),锚框(anchor)是RPN的基础,感受野(receptive field, RF)是anchor的基础。本文介绍感受野及其计算方法、有效感受野概念和理论感受野、Anchor、实际感受野三者之间的关系。
1、感受野
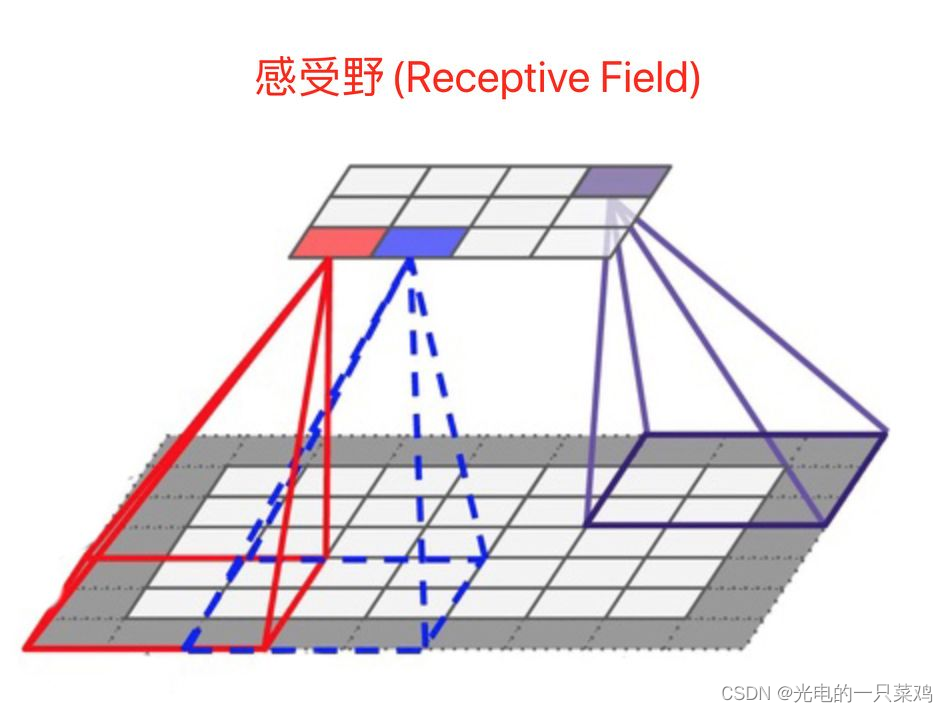
在典型CNN结构中,FC层每个输出节点的值都依赖FC层所有输入,而CONV层每个输出节点的值仅依赖CONV层输入的一个区域,这个区域之外的其他输入值都不会影响输出值,该区域就是感受野。

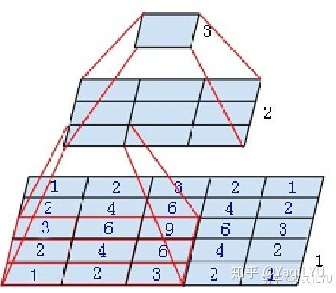
图中是个微型CNN,来自Inception-v3论文,原图是为了说明一个conv5x5可以用两个conv3x3代替,从下到上称为第1, 2, 3层:
1、第2层左下角的值,是第1层左下红框中3x3区域的值经过卷积,也就是乘加运算计算出来的,即第2层左下角位置的感受野是第1层左下红框区域。
2、第3层唯一值,是第2层所有3x3区域卷积得到的,即第3层唯一位置的感受野是第2层所有3x3区域。
3、第3层唯一值,是第1层所有5x5区域经过两层卷积得到的,即第3层唯一位置的感受野是第1层所有5x5区域。
就是这么简单,某一层feature map(特性图)中某个位置的特征向量,是由前面某一层固定区域的输入计算出来的,那这个区域就是这个位置的感受野。任意两个层之间都有位置—感受野对应关系,但我们更常用的是feature map层到输入图像的感受野,如目标检测中我们需要知道feature map层每个位置的特征向量对应输入图像哪个区域,以便我们在这个区域中设置anchor,检测该区域内的目标。
感受野区域之外图像区域的像素不会影响feature map层的特征向量,所以我们不太可能让CNN仅依赖某个特征向量去找到其对应输入感受野之外的目标。这里说“不太可能”而不是“绝无可能”,是因为CNN很强大,且图像像素之间有相关性,有时候感受野之外的目标是可以猜出来的,什么一叶知秋,管中窥豹,见微知著之类,对CNN目标检测都是有可能的,但猜出来的结果并不总是那么靠谱。
感受野有什么用呢?
1、一般task要求感受野越大越好,如图像分类中最后卷积层的感受野要大于输入图像,网络深度越深感受野越大性能越好。
2、密集预测task要求输出像素的感受野足够的大,确保做出决策时没有忽略重要信息,一般也是越深越好。
3、目标检测task中设置anchor要严格对应感受野,anchor太大或偏离感受野都会严重影响检测性能。
两个概念(理论感受野 vs 实际感受野):
理论感受野:某一层feature map中的某一个位置,是由前面某一层固定区域输入计算出来的,那这个固定区域就是这个位置的感受野。PS:上面的感受野定义都是理论感受野。
实际感受野: 实际感受野要小于理论感受野,是在NIPS2016中的Understanding the Effective Receptive Field in Deep Convolutional Neural Networks提出的。文章链接:https://arxiv.org/pdf/1701.04128.pdf
文章主要贡献有以下几点:
1、并不是感受野内所有像素对输出向量的贡献相同,实际感受野是一个高斯分布,有效感受野仅占理论感受野的一部分。

以上就是不同层下的不同的感受野。

使用不同的激活函数与不同的卷积采样方法,产生的实际感受野也不尽相同。其中ReLU的高斯分布没有另外两个平滑,创建了一个较少的高斯分布,ReLU导致很大一部分梯度归零。
这点其实也很好理解,每个卷积层经过多层堆叠,总体感受野就会呈现高斯分布。实际中边缘部分值使用的次数比中心要少的 。

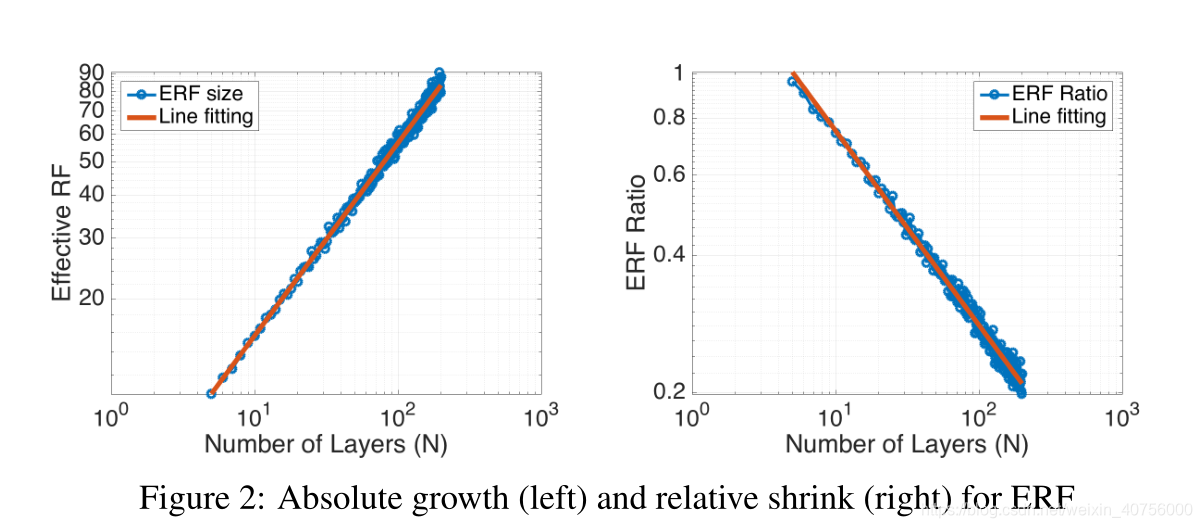
2、另外就是非常关心的问题,实际感受野是如何变化的?实际感受野和理论感受野的关系是什么样的?

文章中也给出了答案,见上图,随着网络层数的加深,实际有效的感受野是程级别增长。而右图展示了随着网络层数的加深,有效感受野占理论感受野的比例是按照级别进行缩减的。其中需要注意的是实际感受野的计算方式:若像素值大于(1-96.45%)的中心像素值,就认为该像素处于实际感受野中。
3、训练的过程中,感受野也会发生变化。

可以看出分类和分割任务经过训练后的感受野都有提升,不过提升幅度不太一样。这也说明了神经网络通过学习,扩大了感受也,能够自适应把越来越大的权重放在感受野之外的像素上。也在一定程度上说明更大感受野的必要性。
2、理论感受野计算
CNN的不同卷积层,用k表示卷积核大小,s表示步长,下标表示层数。
从后往前的计算方式的出发点是:一个conv5x5的感受野等于堆叠两个conv3x3,反之两个堆叠的conv3x3感受野等于一个conv5x5,推广之,一个多层卷积构成的FCN感受野等于一个conv rxr,即一个卷积核很大的单层卷积,其kernelsize=r,padding=P,stride=S。
一些显而易见的结论:
1、初始feature map(也就是原始图片)的感受野默认为1。
2、每经过一个convk*k,s=1的卷积层,感受野 r = r + (k - 1),常用k=3感受野 r = r + 2, k=5感受野r = r + 4。
3、每经过一个convk*k,s=2的卷积层或max/avg pooling层,感受野 r = (r x 2) + (k -2),常用卷积核k=3, s=2,感受野 r = r x 2 + 1,卷积核k=7, s=2, 感受野r = r x 2 + 5。
4、每经过一个maxpool2*2,s=2的max/avg pooling下采样层,感受野 r = r x 2。
5、特殊情况,经过conv1*1,s=1不会改变感受野,经过FC层和GAP层,感受野就是整个输入图像。
6、经过多分枝的路径,按照感受野最大支路计算,shotcut也一样所以不会改变感受野。
7、ReLU, BN,dropout等元素级操作不会影响感受野。
8、全局Stride等于所有层Stride的累乘:
![]()
9、经过的所有层所加padding都可以等效加在输入图像,等效值P,P=floor(r/2-0.5)。
2.1、自上而下感受野计算
PS:理论感受野通用公式: r = r x s + k - s。
逐层计算理论感受野,核心四个公式:
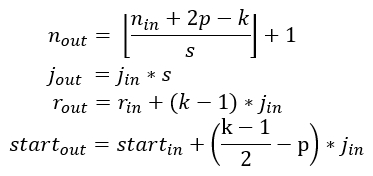
上式中n是feature map的大小,p是padding,k是kernel size,j是jump(前面的S),r是感受野大小,start是第一个特征向量(左上角位置)对应感受野的中心坐标位置。搬运并翻译:
- 公式一是通用计算卷积层输入输出特征图大小的标准公式
- 公式二计算输出特征图的jump,等于输入特征图的jump乘当前卷积层的步进s
- 公式三计算感受野大小,等于输入感受野加当前层的卷积影响因子(k - 1) * jin,注意这里与当前层的步进s没有关系
- 公式四计算输出特征图左上角位置第一个特征向量,对应输入图像感受野的中心位置,注意这里与padding有关系
从以上公式可以看出:start起始值为0.5,经过k=3, p=1时不变,经过k=5, p=2时不变。
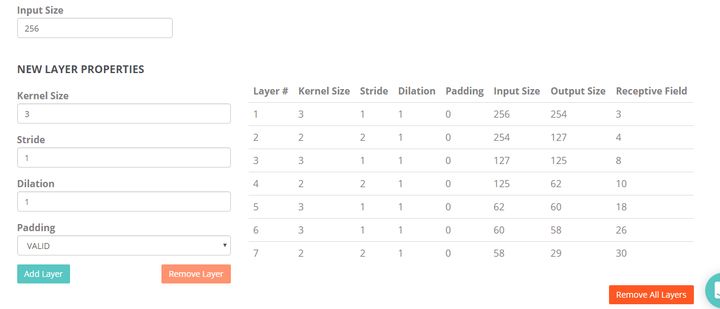
计算示例:

计算出r, j和start之后,所有位置感受野的大小都是r,其他位置的感受野中心是start按照j滑窗得到。这种方法比较规律,推荐编程实现。
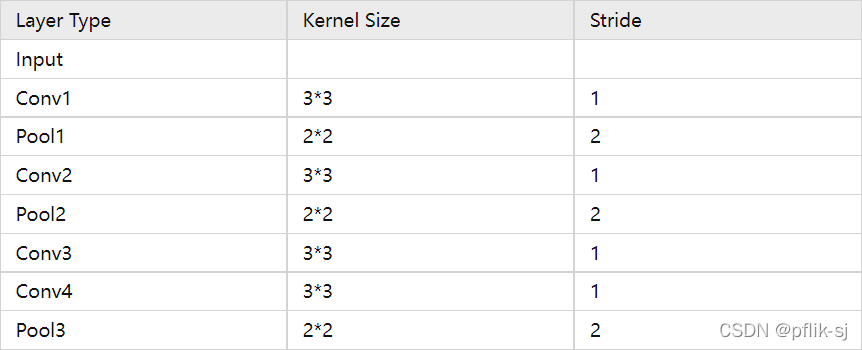
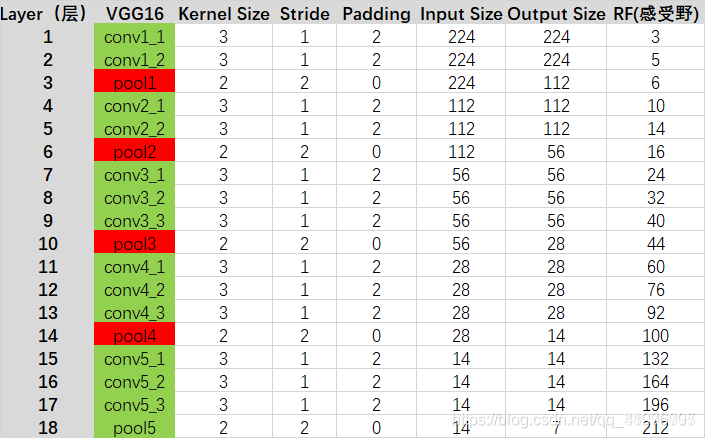
实例,计算VGG16最后一层感受野:

VGG16对应D系列,来计算这一列的感受野(从上往下):
R=(((((1+2+2)x2+2+2)x2+2+2+2)x2+2+2+2)x2+2+2+2)x2=308 S=2x2x2x2x2=32 P=138tensorflow和pytorch已经有人开发出了计算CNN感受野的模型,实际上VGG16感受野没有那么大,下图是可视化一个416x416大小输入图片的感受野,RF实际上只有212x212,也就是下边黄色和蓝色的正方形。
知乎计算方式:https://zhuanlan.zhihu.com/p/44106492
PS:提供一下pytorch和tensorflow计算感受野的库:
Tensorflow:https://github.com/google-research/receptive_field/
Pytorch:https://github.com/Fangyh09/pytorch-receptive-field

以上的计算方式是国内认可度比较高的一种计算方式,在知乎上获得了400+的高赞,但是与谷歌计算出来的结果不一样,所以我就去读了一下谷歌发在Distill上的一篇论文:Computing Receptive Fields of Convolutional Neural Networks,里边非常丰富的讲解了如何计算感受野,包含的情况非常广。先说结论,实际上以上计算方法应该是从下往上进行的,而不是从上往下,另外以上规则只能适合比较有限范围的卷积,而没有一个详细的公式。在讲解下一节以后,我们尝试重新计算VGG的感受野。
2.2、自下而上的计算方法


单路网络中的计算方法:


重新计算VGG16整个模型的感受野:

多路网络:
以上讲解了单路情况下的感受野计算方法,但是现在STOA的卷积网络通常都是拥有多分支的,比如说ResNet、Inception、DenseNet等网络。
多路网络不得不提到对齐问题,感受野是不具有平移不变性,下图就是一个例子:

可以看到,最后一层通过两条不同路径后对应到第一层feature map的感受野的中心是不重合的。这是感受野的一个性质,不过好在大多数现代的网络设计是对齐的,对很多计算机视觉任务来说,都需要对其输出特征,包括目标检测、语义分割、边缘检测、着色等。
在网络对齐时候,所有不同路径都会导致感受野的中心是重合的,所以不同路径必须保持相同的stride。这一点可以观察Inception系列的网络,两条路的Stride是不可能不同的。
在网络对齐的情况下,多路网络的感受野应该是所有分支中最大感受野,比如下边是一个对齐的网络,中心是重合的,感受野的大小就是3。

有了以上的计算方法,我们可以很方便计算所有卷积网络的感受野:

上图是常用分类模型对应的感受野的结果,我们可以发现,随着模型的不断进化,感受野在不增大,在比较新提出的网络中,感受野已经能够覆盖整个输入图像了,这就意味着最终特征图中每个点都会使用到整个图像所有得上下文信息。

上图是感受野大小和在ImageNet上top-1准确率的关系,其中圆圈的大小代表每个网络的浮点运算数量。分类的准确率和感受野大小大体程对数关系,也就是说虽然感受野可以无限增长,越往后,带来的准确率上的提升也就越小,而需要的计算代价会变得更大。
上图MobileNet和VGG16准确率相当,但是MobileNet所需计算量却非常小(约为VGG16的27分之1),这是由于MobileNet使用了大量depth-wise Convolution,这样可以以较小的计算代价来增加模型感受野。这个对比可以表明生成更大感受野的网络可以有更好的识别准确率。
注意:感受野并不是唯一影响准确率的因素,其他因素,比如网络的深度,宽度,残差连接,BatchNorm等也起着非常重要的作用。也就是说,感受野是我们在设计网络的时候需要考虑的一个因素,但还是要综合其他方法。
补充:
除了最普通的卷积,还有空洞卷积、上采样、BatchNorm、Separable Conv的感受野计算需要补充。
- 空洞卷积:引入空洞率a, 经过空洞卷积,kernel size有原来的k变为a*(k-1)+1,所以只要替换原来的公式中的k即可。
- 上采样:一般通过插值来实现,假如a通过2倍上采样得到b,那么认为这个层感受野计算等价于与a的kernel size相等的卷积。(这个地方不是特别理解,按照自己想的,一般upsample不会改变感受野,下边是谷歌论文中关于这部分的讲解,希望能读懂的大佬能联系一下我,我的联系方式在文末)
- 可分离卷积: 等价于普通卷积,并没有变化。
- BatchNorm:推理过程中BN不改变感受野,而训练过程中,BN的感受野是整个输入图像。
- 转置卷积: 会增加感受野,和普通计算方法类似
3、作用
1.目标检测:像SSD、RPN、YOLOv3等都使用了anchor,而anchor的设计正是依据感受野,如果感受野太小,只能观察到局部的特征,不足以得到整个目标的信息。如果感受野过大,则会引入过多噪声和无效信息。Anchor太大或太小均会影响性能。
2.语义分割:最终预测的像素的感受野越大越好,涉及网络一般也是越深越好,这样才能捕获更多的上下文信息,预测才会更准。
3.分类任务:图像分类中最后卷积层的感受野要大于输入图像,网络深度越深,感受野越大,性能越好。
为了更合适的感受野,各种多尺度的模型架构被提出,可以分为图像金字塔和特征金字塔,具体实现方面可以是:1. 采用多尺度输入,如yolov3的multi scale机制。2. 多尺度特征融合,最经典的是FPN。3. 多尺度特征预测融合,如SSD。4. 以上方法的多种组合。
4、关系
在论文 Single Shot Scale-invariant Face Detector 中,说明了目标检测中Anchor, 理论感受野,实际感受野三者的关系。这篇论文主要针对的是中小目标,密集人脸情况下的anchor设置。
Anchor一般是通过先验进行指定的,Anchor与目标的大小和位置越匹配(IOU>0.5or0.7),回归效果就会越好。如果小人脸和anchor的IOU过小,就会造成anchor很难回归到GT上,从而导致Recall过低。

文章中指出了Anchor、理论感受野、实际感受野三者的关系。(a)图中,整个黑色的box是理论感受野,中间的白点是一个高斯分布的实际感受野。(b)图中举了一个例子,黑色点状的框代表是理论感受野的面积,蓝色的代表实际感受野位置,而最合适的anchor就是红色的框,所以关系为:Anchor大小<实际感受野<理论感受野。
SFD是基于SSD进行改进的,SSD中使用了6个层来进行检测,以下是文章中设置内容:

为了探究Anchor和RF的关系,这里使用MATLAB的工具箱来拟合两者关系:

设anchors=x, RFs=y则有如下关系:
![]()
所以y和sqrt(x)大体上是正比例关系。其实这里只是探索一下他们之间的关系,实际感受野实际上依然是一个超参数,我们不可能明确计算出来,然后设置对应的anchor,不过我们了解了这个之后,最起码anchor的限制范围应该是小于理论感受野的。
作者在论文中说明了Anchor设置的理由,Anchor=stride*4, 这样就跟上(c)图一样,这样设置可以保证不同尺度的anchor在图片上采样的密度是一样的。将铺设的anchor的scale值设为大致覆盖到有效感受野的size。这一点并不是特别理解
SFD效果可以说是非常好了,以下是mAP对比图:

5、总结
1、首先,许多经典的网络结构中的这些卷积不是随便决定的,在修改网络的时候不能随便删除。比如在yolov3中,backbone后边的几个卷积再接yolo层这个当时就觉得很随意,但是他是有一定道理的。
2、假如出于对小目标的考虑,想要降低下采样率,那么直接删掉一个maxpool层,或者删掉stride=2的卷积层都是不可取的。通过公式我们知道,stride对一个网络的感受野影响非常大,而且会对后边的网络层的感受野都进行影响,所以要通过使用stride=1的maxpool或者空洞卷积来弥补对感受野带来的损失。
3、实际感受野依然是一个超参数,他是会随着训练的过程发生变化,我们无法准确计算出来实际感受野,但是通过分析anchor,实际感受野和理论感受野,我们知道了anchor
4、自己尝试过使用kmeans算法聚类自己数据集的Anchor,之前两个数据,两次聚类,都出现了自己聚类得到的Anchor不如默认的Anchor得到的结果。之前一直不知道原因在哪里。在总结了感受野以后,我觉得可以合理推测,Anchor应该和实际感受野尽量匹配,但是实际感受野实际上是一个超参数,通过聚类得到的anchor有一定代表性,但是效果反而不如默认的anchor,这是因为我们自己聚类得到的Anchor的范围实际上没有默认的广。比如yolov3-tiny里边的anchor最小是【10,14】最大是【344,319】,经过计算理论感受野是382,按照SFD里边推导得到的公式计算,对应的anchor大小应该为159,如果按照理论感受野的三分之一来计算,大概是127.3。大概在这个范围,自己聚类得到的最大anchor也就是20左右,所以网络如果想要适应(回归)20左右的anchor需要网络更长时间的训练。
最后想推荐一下以上涉及到的三篇文章,都特别有价值,值得多看几遍:
1)S3FD
2)Computing Receptive Fields of Convolutional Neural Networks
3)Understanding the Effective Receptive Field in Deep Convolutional Neural Networks
6、参考文献
SFD论文: https://arxiv.org/abs/1708.05237
YaqiLYU:https://zhuanlan.zhihu.com/p/44106492
感受野计算论文:https://distill.pub/2019/computing-receptive-fields/
感受野推导: "Computing Receptive Fields of Convolutional Neural Networks", Distill, 2019.
一个用来计算感受野的网站:https://fomoro.com/research/article/receptive-field-calculator