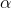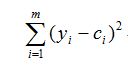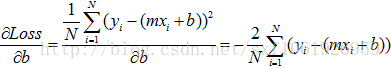1. 原理详解

1.1. 线性回归

假设一个空间中有一堆散点，线性回归的目的就是希望用一条直线，最大程度地“概括”这些散点。它不要求经过每一个散点，但是希望能考虑到每个散点的特点。按照西瓜书的例子就是，好瓜的评判标准y可以由 $x_i$ 表示，也就是说， $f_{good}(x)=w_1x_{色泽}+w_1x_{根蒂}+w_1x_{敲声}+b$ 。
那么我们不难发现，线性回归需要考虑的几个问题：

确定系数 $w_i$ 以及偏置 $b$
如何确定 $f_{good}(x)$ 能很好地概括瓜的特点

1.2. 回归系数

关于这点，我们需要确定，我们算出来的回归系数一定是当前最优的结果，怎么确定呢？

均方误差（西瓜书）
R^2（用于模型评估）

均方误差（MSE）

这个其实就是残差平方和的平均值。
$MSE=\frac{\sum_{i=0}^ny_i-f(x_i)}{n}$

R^2

$R^2=\frac{SSR}{SST}=\frac{SST-SSE}{SST}=1-\frac{SSE}{SST}$

其中，SST是总偏差平方和
$SST=\sum_{i=0}^n(y_i-\bar y)^2$
SSR是回归平方和
$SSR=\sum_{i=0}^n(f(x_i)-\bar y)^2$
SSE是残差平方和
$SSE=\sum_{i=0}^n(y_i-f(x_i))^2$

2. 公式推导

2.1. 单元线性回归

这里我们跟西瓜书一样采取均方误差。

在这里插入图片描述

计算得w与b。

2.2. 多元线性回归

多元线性回归涉及到矩阵运算。

在这里插入图片描述

若X为m * n的矩阵，则 $X^TX$ 为n * n的方阵。 $X^TX$ 的意义在于保持其为可逆矩阵，因为若它不可逆，则导致其行列式为0，就会导致w趋向无穷。

3. 简单实例

3.1. 实例1：一元线性回归

计算这个二元线性回归

index	x	y
1	6	2
2	8	1
3	10	0
4	14	2
5	18	0

我们这里采用几种解法

西瓜书内的公式
最小二乘估计w, b
linalg直接解

# -*- coding:utf-8 -*-
# 2022.09.05
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3Ddef task1_vis(x, y, w, b):fig = plt.figure()ax = fig.add_subplot(1, 1, 1)ax.scatter(x, y)x = np.linspace(0, 20, 100)y = w * x + bax.plot(x, y)# plt.title('Pizza price plotted against diameter')ax.set_xlabel('x', fontdict={'size': 10, 'color': 'black'})ax.set_ylabel('y', fontdict={'size': 10, 'color': 'black'})plt.show()def task1_way1(x, y):w = np.dot(y, (x - x.mean())).sum() / (sum(np.square(x)) - np.square(sum(x)) / x.shape[0])b = sum(y - np.multiply(w, x)) / x.shape[0]print("方法一：\t\tw：{}\tb：{}".format(w, b))def task1_way2(x, y):x_bar = x.mean()y_bar = y.mean()# 计算协方差cov = np.multiply((x - x_bar).transpose(), (y - y_bar)).sum() / (x.shape[0] - 1)var = np.var(x, ddof=1)w = cov / var# w = (y_bar - w * x_bar) / (x.shape[0])b = y_bar - w * x_barprint("方法二：\t\tw：{}\tb：{}".format(w, b))def task1_way3(x, y):from numpy.linalg import lstsqx = np.vstack([x, [1 for i in range(x.shape[0])]])w = lstsq(x.T, y.reshape(-1, 1))[0][0][0]b = lstsq(x.T, y.reshape(-1, 1))[0][1][0]print("方法三：\t\tw：{}\tb：{}".format(w, b))return w, bdef task1():x = np.array([6, 8, 10, 14, 18])y = np.array([7, 9, 13, 17.5, 18])task1_way1(x, y)task1_way2(x, y)w, b = task1_way3(x, y)task1_vis(x, y, w, b)if __name__ == '__main__':task1()

运行结果如下
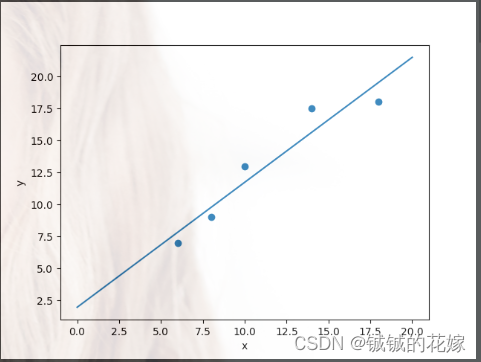
在这里插入图片描述

实例2：多元线性回归

# -*- coding:utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3Ddef task2():from numpy.linalg import invX = np.array([[1, 6, 2], [1, 8, 1], [1, 10, 0], [1, 14, 2], [1, 18, 0]])X[:, 2] = X[:, 1] * X[:, 1]Y = np.array([[7], [9], [13], [17.5], [18]])beita = np.dot(inv(np.dot(np.transpose(X), X)), np.dot(np.transpose(X), Y))print(beita)from numpy.linalg import lstsqprint(lstsq(X, Y)[0])if __name__ == '__main__':# task1()task2()

3.3. 实例3：房价预测

在这里插入图片描述

# -*- coding:utf-8 -*-
# 2022.09.05
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3Ddef task1_vis(x, y, w, b):fig = plt.figure()ax = fig.add_subplot(1, 1, 1)ax.scatter(x, y)y = w * x + bax.plot(x, y, 'r')# plt.title('Pizza price plotted against diameter')ax.set_xlabel('x', fontdict={'size': 10, 'color': 'black'})ax.set_ylabel('y', fontdict={'size': 10, 'color': 'black'})plt.show()def task1_way1(x, y):w = np.dot(y, (x - x.mean())).sum() / (sum(np.square(x)) - np.square(sum(x)) / x.shape[0])b = sum(y - np.multiply(w, x)) / x.shape[0]print("方法一：\t\tw：{}\tb：{}".format(w, b))return w, bdef task1_way2(x, y):x_bar = x.mean()y_bar = y.mean()# 计算协方差cov = np.multiply((x - x_bar).transpose(), (y - y_bar)).sum() / (x.shape[0] - 1)var = np.var(x, ddof=1)w = cov / var# w = (y_bar - w * x_bar) / (x.shape[0])b = y_bar - w * x_barprint("方法二：\t\tw：{}\tb：{}".format(w, b))def task1_way3(x, y):from numpy.linalg import lstsqx = np.vstack([x, [1 for i in range(x.shape[0])]])w = lstsq(x.T, y.reshape(-1, 1))[0][0][0]b = lstsq(x.T, y.reshape(-1, 1))[0][1][0]print("方法三：\t\tw：{}\tb：{}".format(w, b))return w, bdef task1():x = np.array([6, 8, 10, 14, 18])y = np.array([7, 9, 13, 17.5, 18])task1_way1(x, y)task1_way2(x, y)w, b = task1_way3(x, y)task1_vis(x, y, w, b)def task2():from numpy.linalg import invX = np.array([[1, 6, 2], [1, 8, 1], [1, 10, 0], [1, 14, 2], [1, 18, 0]])X[:, 2] = X[:, 1] * X[:, 1]Y = np.array([[7], [9], [13], [17.5], [18]])beita = np.dot(inv(np.dot(np.transpose(X), X)), np.dot(np.transpose(X), Y))print(beita)from numpy.linalg import lstsqprint(lstsq(X, Y)[0])def task3():x_train = np.array([77.36, 116.74, 116.7, 100.68, 116.1, 115.81, 104.24, 106.73, 115.86])y_train = np.array([470, 730, 760, 680, 700, 720, 700, 690, 730])x_test = np.array([56.6, 78.4, 58, 123.5, 56.8, 77, 150.6])w, b = task1_way1(x_train, y_train)y_pre = x_test * w + bprint(y_pre)task1_vis(x_train, y_train, w, b)if __name__ == '__main__':# task1()# task2()task3()