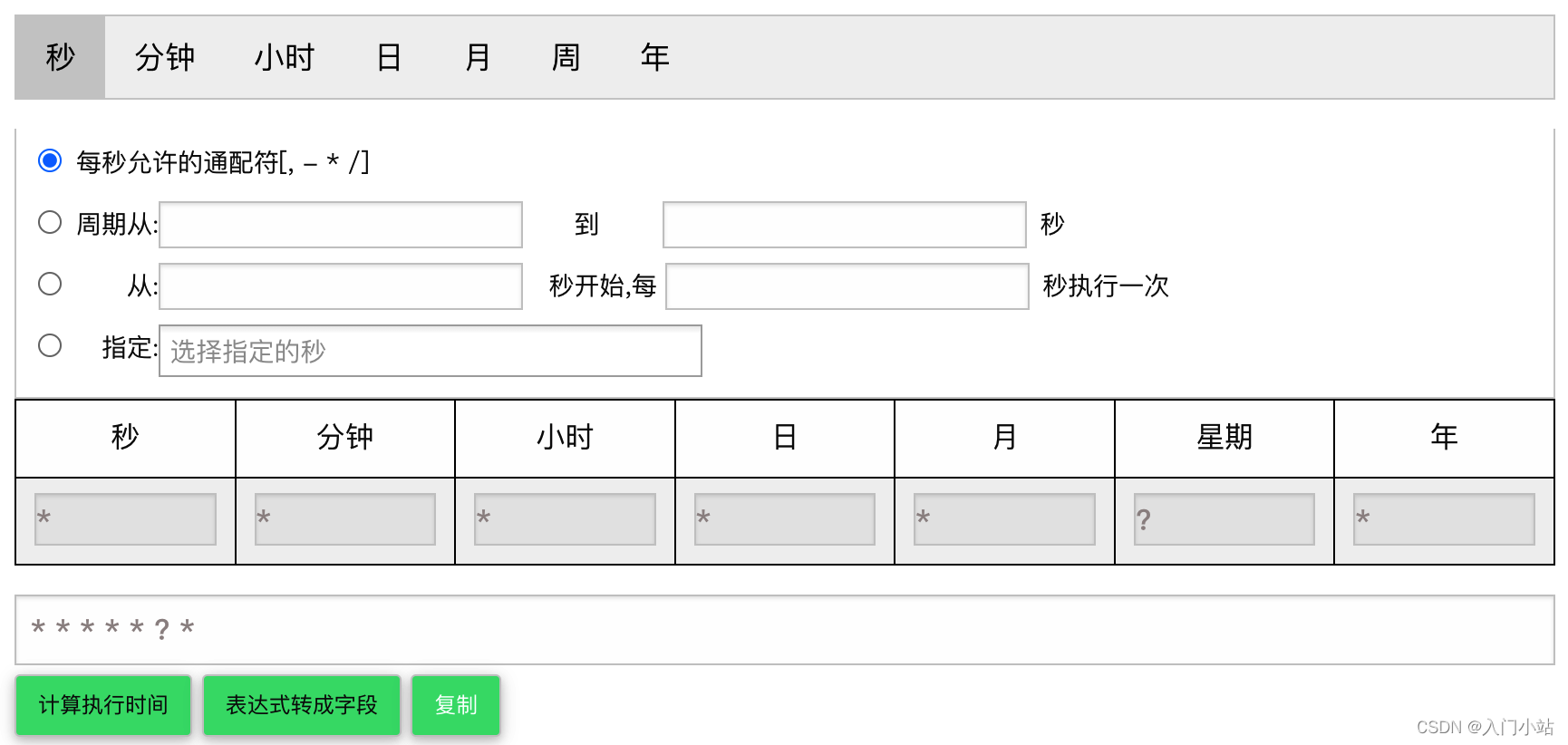
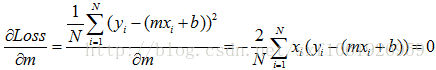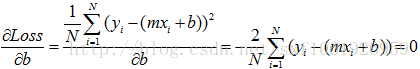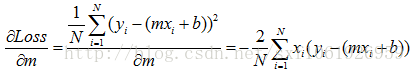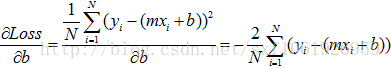线性回归是最简单的一个函数拟合过程，一元线性回归公式为y=ax+b。
我们做拟合，首先需要定义一个损失函数。一般常用的损失函数有：

0-1损失函数和绝对值损失函数

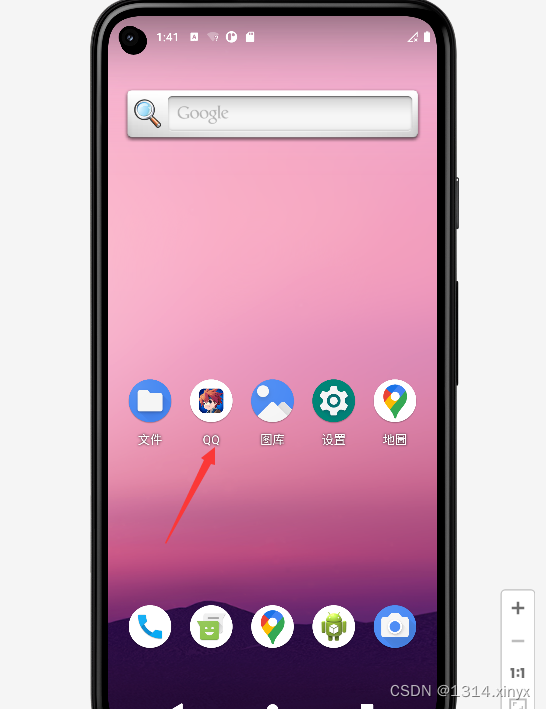
　　0-1损失是指，预测值和目标值不相等为1，否则为0：

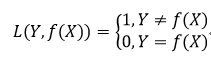
　　感知机就是用的这种损失函数。但是由于相等这个条件太过严格，因此我们可以放宽条件，即满足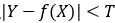时认为相等。

 

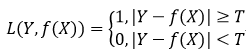
绝对值损失函数：

 

 

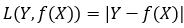
log对数损失函数

　　Logistic回归的损失函数就是对数损失函数，在Logistic回归的推导中，它假设样本服从伯努利分布（0-1）分布，然后求得满足该分布的似然函数，接着用对数求极值。Logistic回归并没有求对数似然函数的最大值，而是把极大化当做一个思想，进而推导它的风险函数为最小化的负的似然函数。从损失函数的角度上，它就成为了log损失函数。

　　log损失函数的标准形式：

 

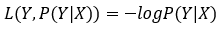
　　在极大似然估计中，通常都是先取对数再求导，再找极值点，这样做是方便计算极大似然估计。损失函数L(Y,P(Y|X))是指样本X在标签Y的情况下，使概率P(Y|X)达到最大值（利用已知的样本分布，找到最大概率导致这种分布的参数值）。

 

平方损失函数

　　最小二乘法是线性回归的一种方法，它将回归的问题转化为了凸优化的问题。最小二乘法的基本原则是：最优拟合曲线应该使得所有点到回归直线的距离和最小。通常用欧式距离进行距离的度量。平方损失的损失函数为：

 

指数损失函数

　　AdaBoost就是一指数损失函数为损失函数的。

　　指数损失函数的标准形式：

 

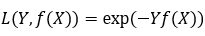
Hinge损失函数

　　Hinge loss用于最大间隔（maximum-margin）分类，其中最有代表性的就是支持向量机SVM。

　　Hinge函数的标准形式：

 

　　

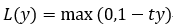
（与上面统一的形式：）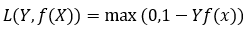

　　其中，t为目标值（-1或+1），y是分类器输出的预测值，并不直接是类标签。其含义为，当t和y的符号相同时（表示y预测正确）并且|y|≥1时，hinge loss为0；当t和y的符号相反时，hinge loss随着y的增大线性增大。

以上参考https://www.cnblogs.com/hejunlin1992/p/8158933.html

作为回归问题，一般我们定义损失函数为均方误差。error = sum((y_true-y_predict)**2)/float(N)y_true真实label，y_predict预测label,N样本总数，**2代表平方，y=ax+b有了损失函数，我们就有了方向，好比大海中的灯塔一样。我们最后需要的函数拟合是最小化损失函数，那么根据大学的高数知识，我们进行求极值，分别对w和b求偏导，我们粘贴已有的公式，m就是上面的w

根据公式，就可以直接求出w和b的取值。一般的话我们使用梯度下降的算法去不断的更新w和b，使误差不断降到最小。

这两个公式就是w和b更新的方向，我们要沿着负梯度方向进行更新，所以w,b应该加上负梯度，lr为学习率

 w = w - (lr * w_gradient)b = b - (lr * b_gradient)具体实现代码如下，另外和sklearn库里面的线性回归做了下对比。发现效果好于库里面的，或许与样本有关系。 

#coding:utf-8
from sklearn.linear_model import  LinearRegression
from sklearn.model_selection import train_test_split
import numpy as np
import matplotlib.pyplot as plt
import pylab
def compute_error(w,b,data_x,data_y):
    total_error= np.sum((data_y - data_x*w -b)**2)
    return total_error/float(len(data_y))

def compute_gradient(w,b,data_x,data_y,lr=0.001):
    data_l = float(len(data_y))
    w_gradient = -(2 / data_l)*data_x*(data_y - data_x*w - b)#最小二乘法对w的偏导公式
    w_gradient = np.sum(w_gradient,axis=0)
    b_gradient = -(2 / data_l) * (data_y - data_x*w-b)#最小二乘法对b的偏导公式
    b_gradient = np.sum(b_gradient,axis=0)
    w = w - (lr * w_gradient)
    b = b - (lr * b_gradient)
    return  w,b

if __name__ == "__main__":
####============================读取数据==============================
    data = np.loadtxt('data.csv', delimiter=',')
    data_x = data[:,0]
    data_y = data[:,1]
    data_x = np.reshape(data_x,(len(data_x),1))
    data_y = np.reshape(data_y, (len(data_y), 1))
    x_train, x_test, y_train, y_test = train_test_split(data_x, data_y,random_state=1,train_size=0.9)
###============================调用库效果不好本数据集中=================================
    # print len(y_train)
    # linreg = LinearRegression()
    # model = linreg.fit(x_train, y_train)
    # print model
    # print linreg.coef_
    # print linreg.intercept_
    # #
    # y_hat = linreg.predict(np.array(x_test))
    # mse = np.average((y_hat - np.array(y_test)) ** 2)  # Mean Squared Error0.869
    # rmse = np.sqrt(mse)  # Root Mean Squared Error##0.932
    # print mse, rmse
    # t = np.arange(len(x_test))
    # plt.plot(t, y_test, 'r-', linewidth=2, label='Test')
    # plt.plot(t, y_hat, 'g-', linewidth=2, label='Predict')
    # plt.legend(loc='upper right')
    # plt.grid()
    # plt.show()
    # pylab.plot(x_test,y_test,'o')
    # pylab.plot(x_test,y_hat,'k-')
    # pylab.show()
##==================梯度更新=================================
    data = np.loadtxt('data.csv', delimiter=',')
    data_x = data[:,0]
    data_y = data[:,1]
    data_x = np.reshape(data_x,(len(data_x),1))
    data_y = np.reshape(data_y, (len(data_y), 1))
    x_train, x_test, y_train, y_test = train_test_split(data_x, data_y,random_state=1,train_size=0.9,shuffle=False)
    print compute_error(0,0,data_x,data_y)
    w = 0
    b = 0
    for i in range(2000):
        w,b = compute_gradient(w=w,b=b,data_x=x_train,data_y=y_train,lr=0.001)
        if i%100==0:
            print 'iter {0}:error={1}'.format(i,compute_error(w=w,b=b,data_x=x_train,data_y=y_train))
    print w,b
    y_pred = x_test * w +b
    mse = np.average((y_pred - np.array(y_test)) ** 2)  # Mean Squared Error#0.674
    rmse = np.sqrt(mse)  # Root Mean Squared Error#0.821
    print "mse",mse
    print "rmse",rmse
    # t = np.arange(len(x_test))
    # plt.plot(t, y_test, 'r-', linewidth=2, label='Test')
    # plt.plot(t, y_pred, 'g-', linewidth=2, label='Predict')
    # plt.legend(loc='upper right')
    # plt.grid()
    # plt.show()
    pylab.plot(x_test,y_test,'o')
    pylab.plot(x_test,y_pred,'k-')
    pylab.show()

训练x，y如下

1    3
1.2    3
1.2    4
1.5    4.5
1.6    4.3
6.5    12
3.6    7.1
2.5    9
5.7    14
6    11
9    17
8.9    17
7.1    15
7    14
2.5    4
0.8    2
0.5    2
3.4    7
3.6    9
5.6    12
6.7    15
6.9    15
7.1    14
7.5    17
7.8    16
8.1    15
8.3    15
8.5    15
8.7    16
8.7    17
8.8    18
8.8    20
8    16
9    19
9.2    18
10.1    20
1.1    3.2
1.6    4.2
4    9
12    25
9.5    20