莫队实际很简(du)单(liu)
依照某位dalao的说法,就是两只小手(two-pointers)瞎跳
一.莫队(静态莫队)
我们以Luogu P3901 数列找不同为例讲一下静态莫队
这道题是个绿题,因为数据比较弱,但真是一道良心的莫队练手题
莫队是由前国家队队长莫涛发明的
莫队算法的精髓就是通过合理地对询问排序,然后以较优的顺序暴力回答每个询问。处理完一个询问后,可以使用它的信息得到下一个询问区间的答案。(两个小手瞎跳)
考虑这个问题:对于上面这道题,我们知道区间[1,5]每个数的数量,如何求出[2,6]每个数的数量
算法1:暴力扫一遍(废话)
算法2:珂以在区间[1,5]的基础上,去掉位置1(即将左端点右移一位),加上位置6(即将右端点右移一位),得到区间[2,6]的答案。
如果按这样写,一种很简单的构造数据就能把时间复杂度把算法2也送上天:先询问[1,2],再询问[99999,100000],多重复几次就gg
但莫队算法是算法2的改进版
要进行合理的排序,使得每两个区间的距离最小
但如何进行合理的排序?
莫队提供了这样一个排序方案:将原序列以$ \sqrt n$为一块进行分块(分块的大小也珂以调整),排序第一关键字是询问的左端点所在块的编号,第二关键字是询问的右端点本身的位置,都是升序。然后我们用上面提到的“移动当前区间左右端点”的方法,按顺序求每个询问区间的答案,移动每一个询问区间左右端点可以求出下一个区间的答案。
这就是一般的莫队排序
inline bool cmp(register query a,register query b)
{return a.bl==b.bl?a.r<b.r:a.bl<b.bl;
}
但由于出题人过于毒瘤
又多出一种优化,叫做奇偶优化
按奇偶块排序。这也是比较通用的。如果区间左端点所在块不同,那么就直接按左端点从小到大排;如果相同,奇块按右端点从小到大排,偶块按右端点从大到小排。
inline bool cmp(register query a,register query b)
{return a.bl!=b.bl?a.l<b.l:((a.bl&1)?a.r<b.r:a.r>b.r);
}
莫队核心代码qaq:
sort(q+1,q+m+1,cmp); //讲询问按上述方法排序
int l=1,r=0; //当前左端点和右端点初值(两只小手two-pointers)
for(register int i=1;i<=m;++i) //对排序后的询问一个个转移
{int ll=q[i].l,rr=q[i].r; //本次询问的区间 //转移,++--这些东西比较容易写错,需要注意 while(l<ll)del(l++);while(l>ll)add(--l);while(r<rr)add(++r);while(r>rr)del(r--);ans[q[i].id]=sth; //询问是排过序的,存到答案数组里需要返回原顺序
}
这样就可以求出答案了!
——可是,这样做的复杂度是什么?
大约是\(O(n \sqrt n)\)
Luogu P3901 AC代码:
#pragma GCC optimize("O3")
#include <bits/stdc++.h>
#define N 100005
using namespace std;
inline int read()
{register int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+ch-'0',ch=getchar();return x*f;
}
int v[N],blocksize=0;
struct query{int l,r,id,bl;
}q[N];
int sum[N];
bool ans[N];
int cnt=0;
inline void add(register int x)
{if(++sum[v[x]]==1)++cnt;
}
inline void del(register int x)
{if(--sum[v[x]]==0)--cnt;
}
inline bool cmp(register query a,register query b)
{return a.bl!=b.bl?a.l<b.l:((a.bl&1)?a.r<b.r:a.r>b.r);
}
int main()
{memset(sum,0,sizeof(sum));int n=read(),m=read();blocksize=sqrt(n);for(register int i=1;i<=n;++i)v[i]=read();for(register int i=1;i<=m;++i){int l=read(),r=read();q[i]=(query){l,r,i,(l-1)/blocksize+1};}sort(q+1,q+m+1,cmp);int l=1,r=0;for(register int i=1;i<=m;++i){int ll=q[i].l,rr=q[i].r;while(l<ll)del(l++);while(l>ll)add(--l);while(r<rr)add(++r);while(r>rr)del(r--);ans[q[i].id]=(cnt==rr-ll+1)?1:0;}for(register int i=1;i<=m;++i)if(ans[i])puts("Yes");elseputs("No");return 0;}
例题:
1.Luogu P3901 数列找不同
讲解比上面暴力
2.Luogu CF375D Tree and Queries
树链剖分(dfs序)后跑莫队
3.Luogu SP3267 DQUERY - D-query
莫队入门题
4.Luogu P1972 [SDOI2009]HH的项链
上面那道题略加卡常
5.Luogu CF86D Powerful array
莫队与小学数学
6.Luogu P1533 可怜的狗狗
莫队+平衡树苟过
7.Luogu P5072 [Ynoi2015]盼君勿忘
题面好评,莫队模板,只是在算贡献时稍微毒瘤
7.Luogu P5071 [Ynoi2015]此时此刻的光辉
题面好评,莫队模板和pollard's Rho的结合
二.动态莫队(单点修改)
写完了上面这道题,可以发现:普通的莫队算法没有支持修改。那么如何改造该算法使它支持修改呢?
莫队俗称优雅的暴力
我们以Luogu P1903 [国家集训队]数颜色 / 维护队列讲解一下动态莫队
那么我们改造莫队算法的思路也只有一个:改造询问排序的方式,然后继续暴力。
首先我们需要把查询操作和修改操作分别记录下来。
在记录查询操作的时候,需要增加一个变量来记录离本次查询最近的修改的位置
然后套上莫队的板子,与普通莫队不一样的是,你需要用一个变量记录当前已经进行了几次修改
每次回答询问时,先从上一个询问的时间“穿越”到当前询问的时间:如果当前询问的时间更靠后,则顺序执行所有修改,直到达到当前询问时间;如果当前询问的时间更靠前,则“时光倒流”,还原所有多余的修改。进行推移时间的操作时,如果涉及到当前区间内的位置的修改,要对答案进行相应的维护。
排序有三个关键字:
1.左端点所在块数 2.右端点所在块数 3.在这次修改之前查询的次数
inline bool cmp(register query a,register query b)
{return a.bll!=b.bll?a.bll<b.bll:(a.blr!=b.blr?a.blr<b.blr:a.pre<b.pre);
}
完整代码,代码中有详细注释
#pragma GCC optimize("O3")
#include <bits/stdc++.h>
#define N 50005
using namespace std;
inline int read()
{register int x=0,f=1;register char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+ch-'0',ch=getchar();return x*f;
}
inline void write(register int x)
{if(!x)putchar('0');if(x<0)x=-x,putchar('-');static int sta[25];int tot=0;while(x)sta[tot++]=x%10,x/=10;while(tot)putchar(sta[--tot]+48);
}
struct change{ //记录修改操作的结构体,place为修改的位置,pre是修改之前的值,suf是修改之后的值 int place,pre,suf;
}cg[N];
struct query{ //记录查询操作的结构体,l,r为查询左右端点,pre表示之前有过几次修改,id表示这是第几次查询,bll,blr表示左右端点所在的块 int l,r,pre,id,bll,blr;
}q[N];
int a[N],blocksize=0,p[1000001],ans[N];
inline bool cmp(register query a,register query b) //按上述三个关键字排序
{return a.bll!=b.bll?a.bll<b.bll:(a.blr!=b.blr?a.blr<b.blr:a.pre<b.pre);
}
int main()
{int n=read(),m=read(),tota=0,totb=0;for(register int i=1;i<=n;++i)a[i]=read();for(register int i=1;i<=m;++i){char ch=getchar();while(ch!='R'&&ch!='Q')ch=getchar();if(ch=='R') //修改 {cg[++tota].place=read(),cg[tota].suf=read();cg[tota].pre=a[cg[tota].place]; //为了方便先在原数组上修改 a[cg[tota].place]=cg[tota].suf;}else{int l=read(),r=read();q[++totb]=(query){l,r,tota,totb,0};}}blocksize=ceil(exp((log(n)+log(tota))/3)); //奇妙的块的大小 for(register int i=1;i<=totb;++i)q[i].bll=(q[i].l-1)/blocksize+1,q[i].blr=(q[i].r-1)/blocksize+1;for(register int i=tota;i>=1;--i) //还原数组 a[cg[i].place]=cg[i].pre;sort(q+1,q+totb+1,cmp); //排序 int l=1,r=0,num=0,ti=0;for(register int i=1;i<=m;++i){int ll=q[i].l,rr=q[i].r,t=q[i].pre;//正常莫队操作 while(ll<l)num+=!p[a[--l]]++;while(ll>l)num-=!--p[a[l++]];while(rr>r)num+=!p[a[++r]]++;while(rr<r)num-=!--p[a[r--]];while(t<ti) //当本次查询时修改的次数小于已经修改的次数,时光倒流 (还原修改) {int pla=cg[ti].place;if(l<=pla&&pla<=r)num-=!--p[a[pla]];a[pla]=cg[ti--].pre;if(l<=pla&&pla<=r)num+=!p[a[pla]]++;}while(t>ti) //当本次查询时修改的次数大于已经修改的次数,穿越 (把该修改的修改) {int pla=cg[++ti].place;if(l<=pla&&pla<=r)num-=!--p[a[pla]];a[pla]=cg[ti].suf;if(l<=pla&&pla<=r)num+=!p[a[pla]]++;}ans[q[i].id]=num;}for(register int i=1;i<=totb;++i){write(ans[i]);printf("\n");}return 0;
}
三、树上莫队
树上莫队,顾名思义就是把莫队搬到树上。
复杂度同序列上的莫队(不带修:\(O(n \sqrt n)\),带修:\(O(n^\frac{5}{3})\))
我们根据Luogu SP10707 COT2 - Count on a tree II来讲树上莫队
题目意思很明确:给定一个n个节点的树,每个节点表示一个整数,问u到v的路径上有多少个不同的整数。
像这种不带修改数颜色的题首先想到的肯定是树套树莫队,那么如何把在序列上的莫队搬到树上呢?
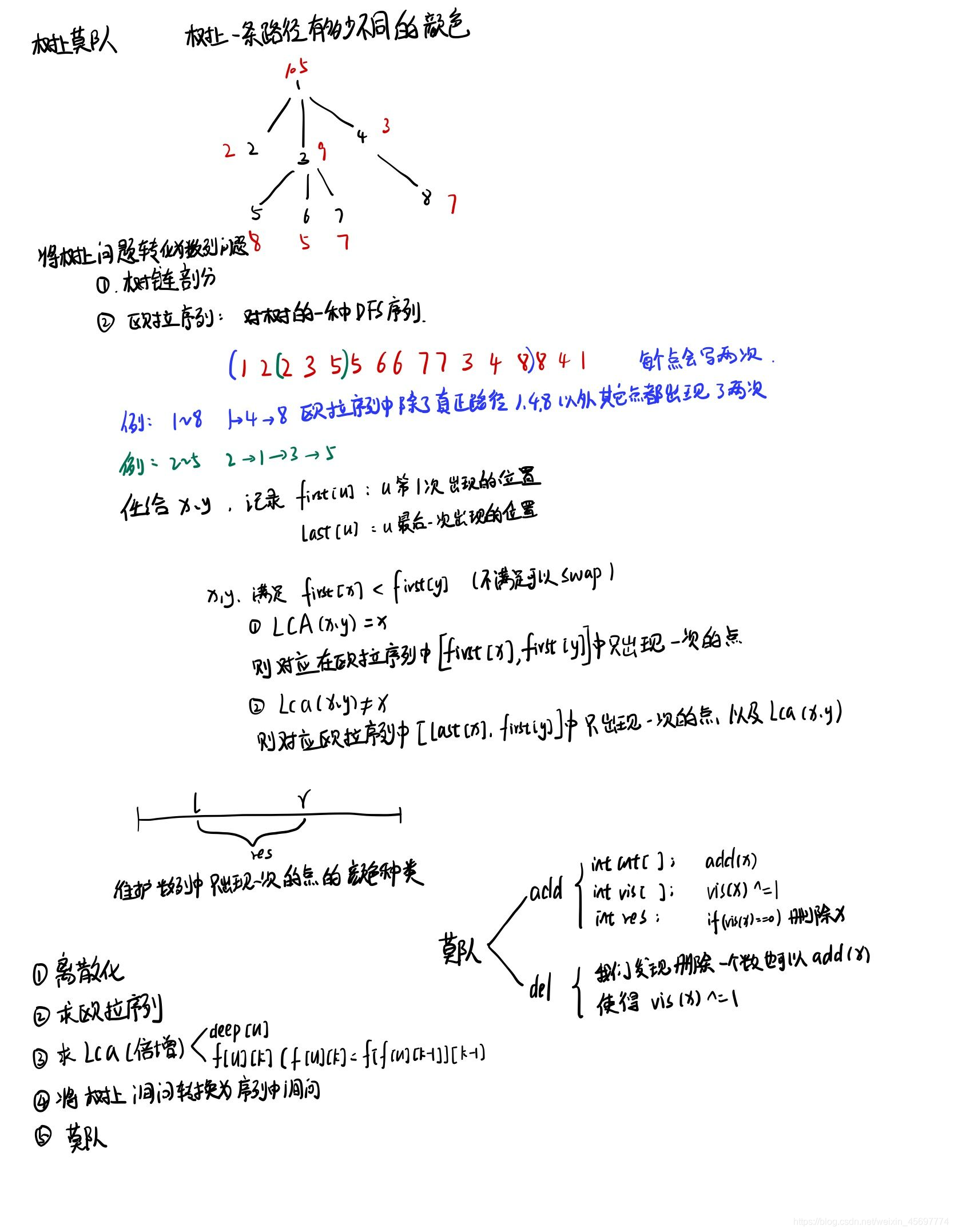
欧拉序
我们考虑用什么东西可以把树上的问题转化到序列上,dfs序是可以的,但是这道题不行(无法搞lca的贡献)
有一种神奇的东西,叫做欧拉序。
它的核心思想是:当访问到点i时,加入序列,然后访问i的子树,当访问完时,再把i加入序列
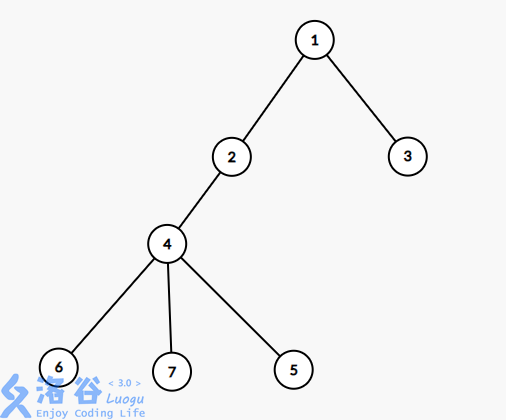
煮个栗子,下面这棵树的欧拉序为
1 2 3 4 4 5 5 6 6 3 7 7 2 1

有了这个有什么用呢?
我们考虑我们要解决的问题:求x到y的路径上有多少个不同的整数
这里我们设st[i]表示访问到i时加入欧拉序的时间,ed[i]表示回溯经过i时加入欧拉序的时间
不妨设st[x]<st[y](也就是先访问x,再访问y)
分情况讨论
若lca(x,y)=x,这时x,y在一条链上,那么st[x]到st[y]这段区间中,有的点出现了两次,有的点没有出现过,这些点都是对答案没有贡献的,我们只需要统计出现过1次的点就好
比如当询问为2,6时,(st[2],st[6])=2 3 4 4 5 5 6 4,5这两个点都出现了两次,因此不统计进入答案
若lca(x,y)≠x,此时x,y位于不同的子树内,我们只需要按照上面的方法统计ed[x]到st[y]这段区间内的点。
比如当询问为4,7时,(ed[4],st[7])=4 5 5 6 6 3 7。大家发现了什么?没错!我们没有统计lca,因此我们需要特判lca
算欧拉序之后可以顺带重链剖分,这样lca就直接树剖来求了qaq
完整代码
#pragma GCC optimize("O3")
#include <bits/stdc++.h>
#define N 40005
#define M 100005
#define getchar nc
using namespace std;
inline char nc(){static char buf[100000],*p1=buf,*p2=buf; return p1==p2&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++;
}
inline int read()
{register int x=0,f=1;register char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+ch-'0',ch=getchar();return x*f;
}
inline void write(register int x)
{if(!x)putchar('0');if(x<0)x=-x,putchar('-');static int sta[20];register int tot=0;while(x)sta[tot++]=x%10,x/=10;while(tot)putchar(sta[--tot]+48);
}
inline void Swap(register int &a,register int &b)
{a^=b^=a^=b;
}
struct edge{int to,next;
}e[N<<1];
int head[N],cnt=0;
inline void add(register int u,register int v)
{e[++cnt]=(edge){v,head[u]};head[u]=cnt;
}
int n,m;
int a[N],date[N];
int dep[N],top[N],siz[N],son[N],fa[N],st[N],ed[N],pot[N<<1],tot=0;
inline void dfs1(register int x,register int f)
{fa[x]=f,siz[x]=1,st[x]=++tot;pot[tot]=x;for(register int i=head[x];i;i=e[i].next)if(e[i].to!=f){dep[e[i].to]=dep[x]+1;dfs1(e[i].to,x);siz[x]+=siz[e[i].to];if(siz[e[i].to]>siz[son[x]])son[x]=e[i].to;}ed[x]=++tot;pot[tot]=x;
}
inline void dfs2(register int x,register int topf)
{top[x]=topf;if(son[x])dfs2(son[x],topf);for(register int i=head[x];i;i=e[i].next)if(e[i].to!=fa[x]&&e[i].to!=son[x])dfs2(e[i].to,e[i].to);
}
inline int Getlca(register int x,register int y)
{while(top[x]!=top[y]){if(dep[top[x]]<dep[top[y]])Swap(x,y);x=fa[top[x]];}return dep[x]<dep[y]?x:y;
}
struct query{int l,r,id,lca;
}q[M];
int bel[N<<1],block;
inline bool cmp(register query a,register query b)
{return bel[a.l]!=bel[b.l]?a.l<b.l:((bel[a.l]&1)?a.r<b.r:a.r>b.r);
}
int ans[M],p[N],vis[N],res=0;
inline void add(register int x)
{res+=!p[x]++;
}
inline void del(register int x)
{res-=!--p[x];
}
inline void Add(register int x)
{vis[x]?del(a[x]):add(a[x]);vis[x]^=1;
}
int main()
{n=read(),m=read();block=sqrt(n);for(register int i=1;i<=n;++i)a[i]=date[i]=read();for(register int i=1;i<=(n<<1);++i)bel[i]=i/block+1;sort(date+1,date+1+n);int num=unique(date+1,date+1+n)-date-1;for(register int i=1;i<=n;++i)a[i]=lower_bound(date+1,date+1+num,a[i])-date;for(register int i=1;i<n;++i){int u=read(),v=read();add(u,v),add(v,u);}dep[1]=1;dfs1(1,0);dfs2(1,1);for(register int i=1;i<=m;++i){int x=read(),y=read();if(st[x]>st[y])Swap(x,y);int lcaa=Getlca(x,y);q[i].id=i;if(lcaa==x)q[i].l=st[x],q[i].r=st[y];elseq[i].l=ed[x],q[i].r=st[y],q[i].lca=lcaa;}sort(q+1,q+1+m,cmp);int l=1,r=0;for(register int i=1;i<=m;++i){int ll=q[i].l,rr=q[i].r;while(l<ll)Add(pot[l++]);while(l>ll)Add(pot[--l]);while(r<rr)Add(pot[++r]);while(r>rr)Add(pot[r--]);if(q[i].lca)Add(q[i].lca);ans[q[i].id]=res;if(q[i].lca)Add(q[i].lca);}for(register int i=1;i<=m;++i)write(ans[i]),puts("");return 0;
}
四、回滚莫队
1.我们以块编号为第一关键字排序,右端点位置为第二关键字排序
2.询问时依次枚举区间,我们保留右端点的移量(右边单增),左端点则每次在这一个块中来回移动
3.下一个块时,清空统计答案重做
所以对于每一个块:左端点每次操作\(O(\sqrt n)\),右端点总共移n,均摊\(O(\sqrt n)\),因此时间复杂度保证了\(O(n\sqrt n)\)
完整代码Luogu AT1219 歴史の研究
#include <bits/stdc++.h>
#define N 100005
#define ll long long
using namespace std;
inline ll read()
{register ll x=0,f=1;register char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+ch-'0',ch=getchar();return x*f;
}
inline void write(register ll x)
{if(!x)putchar('0');if(x<0)x=-x,putchar('-');static int sta[36];int tot=0;while(x)sta[tot++]=x%10,x/=10;while(tot)putchar(sta[--tot]+48);
}
inline ll Max(register ll a,register ll b)
{return a>b?a:b;
}
struct query{int l,r,id,bll,blr;
}q[N];
inline bool cmp(register query a,register query b)
{return a.bll==b.bll?a.r<b.r:a.bll<b.bll;
}
int n,m,blocksize;
int a[N],v[N];
ll sum[N],num[N],ans[N];
ll pre,now;
inline void add(register int x)
{sum[x]+=v[x];now=Max(now,sum[x]);
}
inline void del(register int x)
{sum[x]-=v[x];
}
int main()
{n=read(),m=read();blocksize=sqrt(n);for(register int i=1;i<=n;++i)v[i]=a[i]=read();sort(v+1,v+1+n);int tot=unique(v+1,v+1+n)-v-1;for(register int i=1;i<=n;++i)a[i]=lower_bound(v+1,v+1+tot,a[i])-v;for(register int i=1;i<=m;++i){int l=read(),r=read();q[i]=(query){l,r,i,(l-1)/blocksize+1,(r-1)/blocksize+1};}sort(q+1,q+1+m,cmp);int l=1,r=0,pos=0;for(register int i=1;i<=m;++i){int ql=q[i].l,qr=q[i].r;if(q[i].bll!=q[i-1].bll){memset(sum,0,sizeof(sum));pre=now=0;l=pos=q[i].bll*blocksize+1;r=l-1;}if(q[i].bll==q[i].blr){ll cur=0;for(register int j=ql;j<=qr;++j){num[a[j]]+=v[a[j]];cur=Max(cur,num[a[j]]);}for(register int j=ql;j<=qr;++j)num[a[j]]-=v[a[j]];ans[q[i].id]=cur;continue;}while(r<qr)add(a[++r]);pre=now;while(l>ql)add(a[--l]);ans[q[i].id]=now;while(l<pos)del(a[l++]);now=pre;}for(register int i=1;i<=m;++i)write(ans[i]),puts("");return 0;
}