upd：2021-08-11：重新对博客进行了外观美化修正，以及新增树上莫队
upd：2021-08-19：新增回滚莫队

问题引入

给定一个大小为$N$的数组，数组中所有元素的大小$\le N$。你需要回答$M$个查询。
每个查询的形式是$L,R$。你需要回答在范围$[L,R]$中至少重复$2$次的数字的个数

---

如果按照以往的想法，就会是$O(n^2)$的暴力枚举

for ( int i = 1;i <= Q;i ++ ) {scanf ( "%d %d", &l, &r );for ( int j = l;j <= r;j ++ ) {count[a[j]] ++;if ( count[a[j]] == 3 )result ++;}}

就算加一些优化，用$l,r$采取指针转移，但总归上还是在$[1,n]$区间内进行移动

最坏多半也是逼近于$O(n^2)$​

void add ( int x ) {count[a[x]] ++;if ( count[a[x]] == 3 )result ++;
}
void removed ( int x ) {count[a[x]] --;if ( count[a[x]] == 2 )result --;
}
for ( int i = 1;i <= m;i ++ ) {scanf ( "%d %d", &l, &r );while ( curl < l )removed ( curl ++ );while ( curl > l )add ( -- curl );while ( curr > r )removed ( curr -- );while ( curr < r )add ( ++ curr );printf ( "%d\n", result );
}

add ​添加该位置的元素到当前集合内，并且更新答案

remove 从当前集合内删除该位置的元素，并更新答案

---

那么这个时候莫队算法就重磅登场了

为什么叫做莫队算法呢？

据说算法是由之前的国家队队长莫涛发明的，他的队友平日里称他为莫队，所以称之为莫队算法

---

介绍莫队算法及其实现过程

莫队算法就是一个离线算法，仅仅调整了处理查询的顺序

实现过程如下：

• 将给定的输入数组分为$\sqrt{n}$​​​​​块。每一块的大小为 $\frac{n}{\sqrt{n}}$​

  每个$L$​​​​落入其中的一块，每个$R$也落入其中的一块

  如果某查询的$L$​​​落在第$i$​​块中，则该查询属于第$i$​块​​

• 所有的询问首先按照所在块的编号升序排列（所在块的编号是指询问的L属于的块）

  如果编号相同，则按R值升序排列

• 莫队算法将依次处理第$1$块中的查询，然后处理第$2$块$...$直到最后一块

  有很多的查询属于同一块

e.g.

假设我们有$3$​​个大小为$3$​的块$(0-2,3-5,6-8)$： { 0 , 3 } { 1 , 7 } { 2 , 8 } { 7 , 8 } { 4 , 8 } { 4 , 4 } { 1 , 2 } \{0,3\} \{1, 7\} \{2, 8\} \{7, 8\} \{4, 8\} \{4, 4\} \{1, 2\} {0,3}{1,7}{2,8}{7,8}{4,8}{4,4}{1,2}

先根据所在块的编号重新排列它们

• 第$1$块： { 0 , 3 } { 1 , 7 } { 2 , 8 } { 1 , 2 } \{0, 3\} \{1, 7\} \{2, 8\} \{1, 2\} {0,3}{1,7}{2,8}{1,2}
• 第$2$块： { 4 , 8 } { 4 , 4 } \{4, 8\} \{4, 4\} {4,8}{4,4}
• 第$3$​块： { 7 , 8 } \{7, 8\} {7,8}

接下来按照R的值重新排列

• 第一块： { 1 , 2 } { 0 , 3 } { 1 , 7 } { 2 , 8 } \{1, 2\} \{0, 3\} \{1, 7\} \{2, 8\} {1,2}{0,3}{1,7}{2,8}
• 第二块： { 4 , 4 } { 4 , 8 } \{4, 4\} \{4, 8\} {4,4}{4,8}
• 第三块： { 7 , 8 } \{7, 8\} {7,8}

上述过程只是重新排列了查询的顺序

---

时间复杂度

我们说了这么多，选用莫队算法无非就是想把时间复杂度给降下来

接下来我们来看看真正莫队的时间复杂度是多少，其实我看了很多博客也是有点懵逼

上面的代码就是起一个铺垫作用，所有查询的复杂性是由$4$个``while`循环决定的

前$2$​​个while循环可以理解为左指针curl的移动总量

后$2$​​个 while循环可以理解为右指针curr的移动总量

这两者的和将是总复杂性

---

先算右指针

对于每个块，查询是递增的顺序排序，所以右指针curr按照递增的顺序移动

在下一个块的开始时，指针可能在最右端，将移动到下一个块中的最小的$R$处

又可以从本块最左端移动到最右端

这意味着对于一个给定的块，右指针移动的量是$O(n)$（curr可以从$1$跑到最后的$n$）

我们有$O(\sqrt{n})$​块，所以总共是$O(n\sqrt{n})$​​

---

接下来看看左指针怎样移动

对于每个块，所有查询的左指针落在同一个块中，从一个查询移动到下一个查询左指针会移动

但由于前一个$L$​与下一个$L$在同一块中，此移动是$O(\sqrt{n})$​​​（块的大小）

在每一块中左指针的移动总量是$O(Q\sqrt{n})$​​，($Q$是落在那个块的查询的数量)

对于所有的块，总的复杂度为$O(m\ast \sqrt{n})$​​

---

综上，总复杂度为$O((n+m)\ast \sqrt{n})=O(n\ast \sqrt{n})$​

实在无法理解就跳过吧（如果有通俗易懂的解释欢迎评论)

莫队算法适用范围

首先莫队算法是一个离线算法，所以如果问题是在线操作带修或者强制特殊的顺序

莫队就失去了它的效应

---

其次一个重要的限制性：add和remove的操作

当有些题目的add和remove耗时很大，$O(\sqrt{N})$​​​​时就应该思考能否卡过

因为莫队本身就是一种优美的暴力而已

但是还是有很大一部分区间查询的题可以由莫队进行完成

莫队奇偶优化

sqt = sqrt( n )
bool cmp( node x, node y ) {return ( x.l / sqt == y.l / sqt ) ? ( ( ( x.l / sqt ) & 1 ) ? x.r < y.r : x.r > y.r ) : x.l < y.l;
}

---

普通莫队：小B的询问

小B有一个序列，包含N个1~K之间的整数。他一共有M个询问，
每个询问给定一个区间[L…R]，求Sigma(c(i)^2)的值,
其中i的值从1到K，其中c(i)表示数字i在[L…R]中的重复次数。
小B请你帮助他回答询问。

输入格式
第一行，三个整数N、M、K。
第二行，N个整数，表示小B的序列。
接下来的M行，每行两个整数L、R。
输出格式
M行，每行一个整数，其中第i行的整数表示第i个询问的答案。

输入输出样例
输入
6 4 3
1 3 2 1 1 3
1 4
2 6
3 5
5 6
输出
6
9
5
2
说明/提示
对于全部的数据，1<=N、M、K<=50000

简单题解

说了是算法模板入门题，肯定不会把你拒之门外，还是要让你摸摸门的

这个题就是要简单处理一下$\sum c_i^2$​，当$c_i\pm 1$​时，答案会发生怎样的转化？

完全平方公式大家都会吧！！！👇

$$(c[i]-1{)}^2=c[i{]}^2-2\ast c[i]+1$$​

$$(c[i]+1{)}^2=c[i{]}^2+2\ast c[i]+1$$

#include <cmath>
#include <cstdio>
#include <algorithm>
using namespace std;
#define LL l;ong long
#define MAXN 50005
struct node {int l, r, num;
}G[MAXN];
int n, m, k, apart, curl = 1, curr; 
int a[MAXN], cnt[MAXN];
LL result;
LL ans[MAXN];bool cmp ( node x, node y ) {return ( x.l / apart == y.l / apart ) ? x.r < y.r : x.l < y.l;
}void add ( int x ) {result += ( cnt[a[x]] << 1 ) + 1;cnt[a[x]] ++;
}
void removed ( int x ) {result -= ( cnt[a[x]] << 1 ) - 1;cnt[a[x]] --;
}int main() {scanf ( "%d %d %d", &n, &m, &k );for ( int i = 1;i <= n;i ++ )scanf ( "%d", &a[i] );apart = sqrt ( n );for ( int i = 1;i <= m;i ++ ) {scanf ( "%d %d", &G[i].l, &G[i].r );G[i].num = i;}sort ( G + 1, G + m + 1, cmp );for ( int i = 1;i <= m;i ++ ) {int l = G[i].l, r = G[i].r;while ( curl < l ) {removed ( curl ++ );}while ( curl > l ) {add ( -- curl );}while ( curr > r ) {removed ( curr -- );}while ( curr < r ) {add ( ++ curr );}ans[G[i].num] = result;}for ( int i = 1;i <= m;i ++ )printf ( "%lld\n", ans[i] );return 0;
}

树上莫队：SP10707 COT2 - Count on a tree II

顾名思义就是把序列莫队搬到树上实现

分块的大小以及移动的操作与序列莫队无差别

唯一的区别就在于询问的l,r

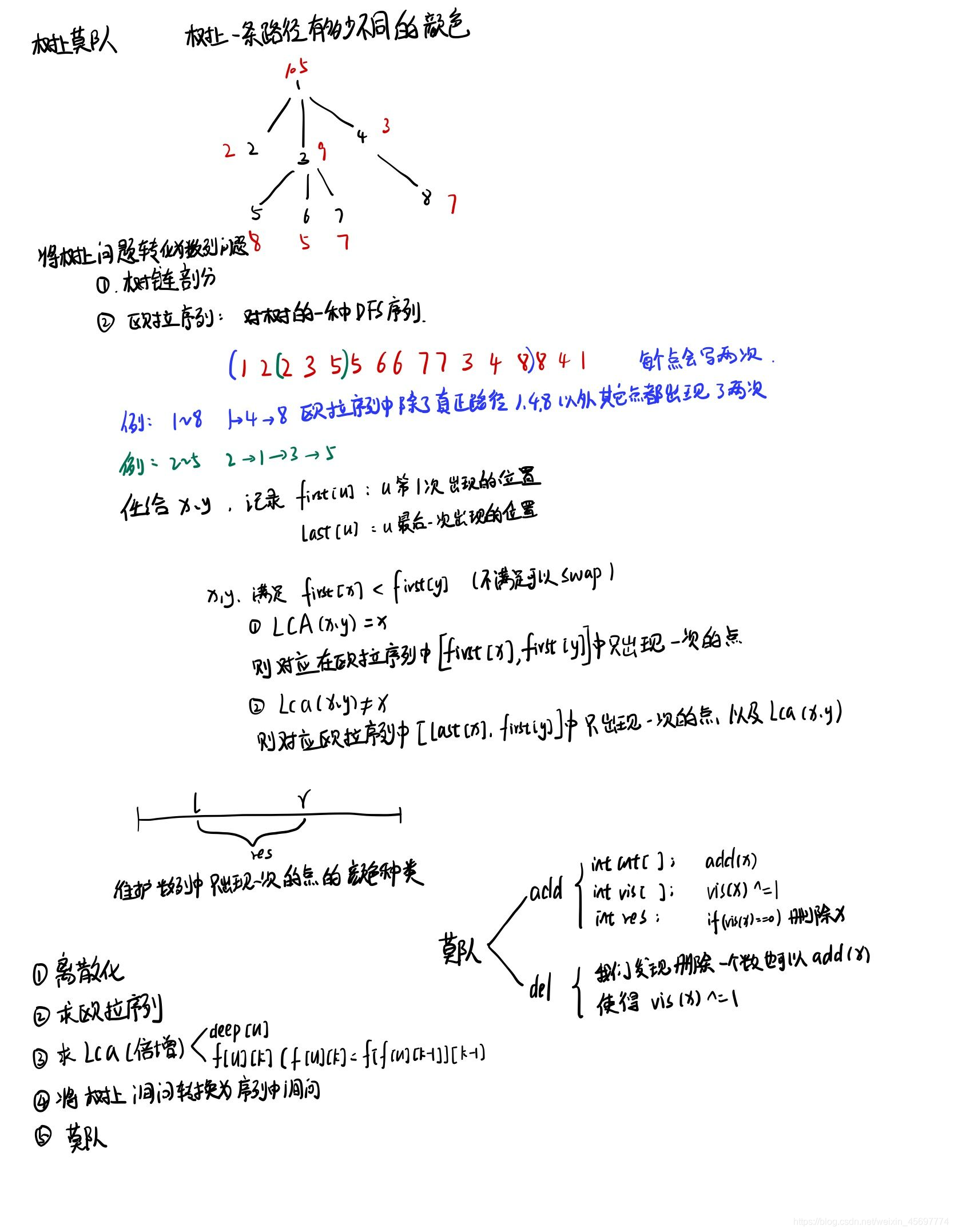
在树上莫队询问的$l,r$​要用欧拉序进行重新编号

e.g.

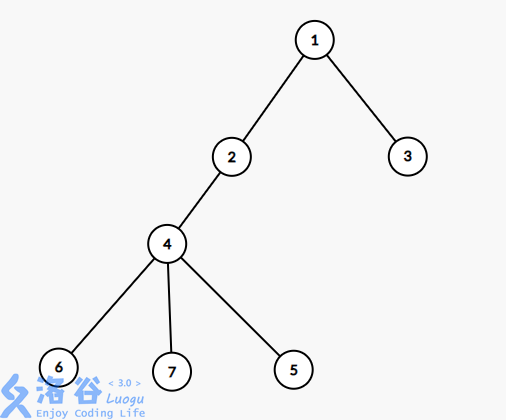
原图的欧拉序为1,2,4,6,6,7,7,5,5,4,2,3,3,1，对于点$i$，$l_i:$ 第一次访问$i$，$r_i:$ 最后一次访问$i$

树上莫队就是用欧拉序的$l_i,r_i$代替访问的$i$

对于查询的(u,v)有两种情况

• 是直系祖先关系（假设$u$是$v$的祖先）

  e.g. : $u=2,v=7$​​，拿出$[l_u,l_v]$​代替$u,v$​

  欧拉序为2,4,6,6,7

• 不隶属同一棵子树（假设$l_u<l_v$）

  e.g : $u=7,v=3$​，拿出$[r_u,l_v]$​

  欧拉序为7,5,5,4,2,3

不在路径上的点经过了恰好两次，真正在路径上的点都恰好只出现一次；对于不同子树的两点需要额外加上lca

source

#include <cmath>
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
#define maxn 40005
#define maxm 100005
vector < int > G[maxn];
int n, Q, B, cnt, ans;
bool vis[maxn];
int c[maxn], MS[maxn], tot[maxn], ret[maxm];
int dep[maxn], l[maxn], r[maxn], id[maxn << 1];
int f[maxn][20];
struct node {int l, r, id, lca;
}q[maxm];void dfs( int u, int fa ) {dep[u] = dep[fa] + 1, l[u] = ++ cnt, id[cnt] = u;for( int i = 1;i <= 16;i ++ )f[u][i] = f[f[u][i - 1]][i - 1];for( auto v : G[u] ) {if( v == fa ) continue;else f[v][0] = u, dfs( v, u );}r[u] = ++ cnt, id[cnt] = u;
}int get_lca( int u, int v ) {if( dep[u] < dep[v] ) swap( u, v );for( int i = 16;~ i;i -- )if( dep[f[u][i]] >= dep[v] ) u = f[u][i];if( u == v ) return u;for( int i = 16;~ i;i -- )if( f[u][i] != f[v][i] ) u = f[u][i], v = f[v][i];return f[u][0];
}void Delete( int x ) { if( -- tot[c[x]] == 0 ) ans --; }void Insert( int x ) { if( ++ tot[c[x]] == 1 ) ans ++; }void modify( int x ) { vis[x] ? Delete( x ) : Insert( x ); vis[x] ^= 1; }int main() {scanf( "%d %d", &n, &Q );for( int i = 1;i <= n;i ++ )scanf( "%d", &c[i] ), MS[i] = c[i];sort( MS + 1, MS + n + 1 );int m = unique( MS + 1, MS + n + 1 ) - MS - 1;for( int i = 1;i <= n;i ++ )c[i] = lower_bound( MS + 1, MS + m + 1, c[i] ) - MS;B = sqrt( n );for( int i = 1, u, v;i < n;i ++ ) {scanf( "%d %d", &u, &v );G[u].push_back( v );G[v].push_back( u );}dfs( 1, 0 );for( int i = 1, u, v;i <= Q;i ++ ) {scanf( "%d %d", &u, &v );q[i].id = i;if( l[u] > l[v] ) swap( u, v );int lca = get_lca( u, v );if( u == lca ) q[i].l = l[u], q[i].r = l[v], q[i].lca = 0;else q[i].l = r[u], q[i].r = l[v], q[i].lca = lca;}sort( q + 1, q + Q + 1, []( node x, node y ) { return ( x.l / B == y.l / B ) ? ( x.r < y.r ) : ( x.l < y.l ); } );int curl = 1, curr = 0;for( int i = 1;i <= Q;i ++ ) {while( curl < q[i].l ) modify( id[curl ++] );while( q[i].l < curl ) modify( id[-- curl] );while( curr < q[i].r ) modify( id[++ curr] );while( q[i].r < curr ) modify( id[curr --] );if( q[i].lca ) modify( q[i].lca );ret[q[i].id] = ans;if( q[i].lca ) modify( q[i].lca );}for( int i = 1;i <= Q;i ++ )printf( "%d\n", ret[i] );
}

回滚莫队：[PA2011]Kangaroos

普通莫队是能做到快速增添和删减操作的

但有些题目在区间转移时，可能会出现增加或者删除无法实现的问题

在只有增加不可实现或者只有删除不可实现的时候，就可以使用回滚莫队

同样在$O(n\sqrt{n})$的时间内解决问题

回滚莫队的核心思想就是既然只能实现一个操作，那么就只使用一个操作，剩下的交给回滚解决

回滚莫队分为只使用增加操作的回滚莫队和只使用删除操作的回滚莫队

以只使用添加操作的回滚莫队为例

• 首先仍是按照区间左端点分块排序，然后右端点为第二关键字
• 枚举区间左端点的块
  • 对于询问的左右端点都在同一区间的直接暴力做
  • 将左端点都在该块的按右端点升序排序
  • 每次都是右端点右移，加入答案
  • 左端点每次都回滚到这个块的末尾，然后暴力的往前移到本次询问的左端点处，记录这一路上的答案，但是不像右端点一样是永久的
    再回退到块末尾，这样的时间复杂度，$m$个询问，每次询问左端点最多暴力移整个区间$\sqrt{n}$，还是根号级别的复杂度
• 到下一块的时候，$l,r$一起遍历了整个区间，扔掉所有的标记那些，然后手动重置为初始局面

只支持删除的话，我想应该就是右端点$r$递减，不断前移，然后还是左端点$l$在块中反复移动清空

可以看一下这道题$\to$ 回滚莫队的例题——历史研究

Kangaroos比较难一点

区间过大，实际上区间相交只关系左右端点的大小关系，所以先离散化区间的端点，最多只有$2n$个

然后按询问左端点分块，将询问挂到块上

接下来就是回滚莫队问题了

这道题主要是要维护最大连续区间

每次将新增区间的下标扔进去的时候，更新

可以用线段树维护最大连续区间，但是实际上可以用$\mathrm{l}[],\mathrm{r}[]$数组来维护左右端点，省去$\mathrm{l}\mathrm{o}\mathrm{g}$

这只是简单口胡，看不懂可以看代码，代码里有详细注释

#include <cmath>
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
#define maxn 200005
#define maxB 320
struct node {int l, r, id;node(){}node( int L, int R, int ID ) {l = L, r = R, id = ID;}
}t[maxn];
struct Node {int val, id;Node(){}Node( int Val, int ID ) {val = Val, id = ID;}
}x[maxn];
vector < node > q[maxB];
int n, m, ans, top;
int block[maxn], L[maxB], R[maxB], l[maxn], r[maxn], ret[maxn];bool operator < ( Node s, Node t ) {return s.val == t.val ? s.id < t.id : s.val < t.val;
}struct opt {//记录操作前的相关信息 方便回滚 //flag 0:左 1:右 记录被更改的是哪边 int flag, pos, lst, ans;opt(){}opt( int  Flag, int Pos, int Lst, int Ans ) {flag = Flag, pos = Pos, lst = Lst, ans = Ans;}
}s[maxn << 4];
//l[i]:在当前已加入区间中i区间所能连的最左边区间下标 -> [l(i),i]的所有区间都与当前查询区间有交 
//r[i]:在当前已加入区间中i区间所能连的最右边区间下标 -> [i,r(i)]的所有区间都与当前查询区间有交 
void add( int i ) {if( l[i] || r[i] ) return;//已经算过了i的贡献 if( ! l[i - 1] and ! r[i + 1] ) {//左右的区间都还没有被加进来//只能自己这一个区间 长度为1 s[++ top] = opt( 0, i, l[i], ans );s[++ top] = opt( 1, i, r[i], ans );l[i] = r[i] = i, ans = max( ans, 1 );}else if( ! l[i - 1] ) {//i+1的区间被加入了 可以往左延伸和i接上 s[++ top] = opt( 0, r[i + 1], l[r[i + 1]], ans );s[++ top] = opt( 1, i, r[i], ans );r[i] = r[i + 1], l[r[i + 1]] = i;ans = max( ans, r[i] - i + 1 );}else if( ! r[i + 1] ) {//i-1的区间被加入了 可以往右延伸和i接上 s[++ top] = opt( 1, l[i - 1], r[l[i - 1]], ans );s[++ top] = opt( 0, i, l[i], ans );l[i] = l[i - 1], r[l[i - 1]] = i;ans = max( ans, i - l[i] + 1 );}else {//i-1 i+1都被加入 直接左右连接拼起来 s[++ top] = opt( 0, r[i + 1], l[r[i + 1]], ans );s[++ top] = opt( 1, l[i - 1], r[l[i - 1]], ans );s[++ top] = opt( 0, i, l[i], ans );s[++ top] = opt( 1, i, r[i], ans );//都连起来了 也没有i什么事了 所以随便记录i的一边l/r有值 下次就可以在第一个if语句直接return l[r[i + 1]] = l[i - 1], r[l[i - 1]] = r[i + 1], l[i] = r[i] = i;ans = max( ans, r[i + 1] - l[i - 1] + 1 );		}
}void remove( int lst ) {while( top > lst ) {if( ! s[top].flag ) l[s[top].pos] = s[top].lst;else r[s[top].pos] = s[top].lst;ans = s[top --].ans; }
}void solve( int id ) {remove( 0 );//移动到新块 莫队里的东西清空 for( int i = 1;i <= n;i ++ ) if( t[i].l < L[id] && R[id] < t[i].r )//完全覆盖该块且不在块内的区间一定会对块内所挂询问产生贡献 add( t[i].id );sort( q[id].begin(), q[id].end(), []( node x, node y ) { return x.r < y.r; } );//将块内询问按照右端点排序 只增加的回滚莫队 int lst = top;for( node now : q[id] ) //计算整个区间都在块内的询问的答案if( now.r > R[id] ) continue;else {for( int i = L[id];i <= R[id];i ++ )if( now.l <= t[x[i].id].r && t[x[i].id].l <= now.r )//与查询区间有交 可能会为答案贡献的区间 add( x[i].id );ret[now.id] = ans;remove( lst ); }remove( 0 );int cur = R[id];//处理r在其他块递增的询问 先把指针拨到块的最后for( int i = 1;i <= n;i ++ )if( t[i].l <= R[id] && R[id] <= t[i].r )//一定会与后面的查询有交点 R[id]add( t[i].id );for( node now : q[id] )if( now.r <= R[id] ) continue;else {while( cur < now.r ) add( x[++ cur].id );lst = top;for( int i = R[id];i >= now.l;i -- )//回滚莫队 滚到当前询问的左端 add( x[i].id );ret[now.id] = ans;remove( lst );//返回 回滚 抵消 }
}int main() {scanf( "%d %d", &n, &m );for( int i = 1, l, r;i <= n;i ++ ) {scanf( "%d %d", &l, &r );x[i] = Node( l, i );x[i + n] = Node( r, i );t[i] = node( l, r, i );}//为了块的大小能开出来 1e9首先要离散化 sort( x + 1, x + ( n << 1 ) + 1 );for( int i = 1;i <= n;i ++ ) {t[i].l = lower_bound( x + 1, x + ( n << 1 | 1 ), Node( t[i].l, 0 ) ) - x;t[i].r = upper_bound( x + 1, x + ( n << 1 | 1 ), Node( t[i].r, 1e9 ) ) - x - 1;}int N = n << 1;int B = sqrt( N );for( int i = 1;i <= N;i ++ )block[i] = ( i - 1 ) / B + 1;//L,R 记录块的左右端点 for( int i = N;i;i -- ) L[block[i]] = i;for( int i = 1;i <= N;i ++ ) R[block[i]] = i;for( int i = 1, l, r;i <= m;i ++ ) {scanf( "%d %d", &l, &r );l = lower_bound( x + 1, x + ( n << 1 | 1 ), Node( l, 0 ) ) - x;r = upper_bound( x + 1, x + ( n << 1 | 1 ), Node( r, 1e9 ) ) - x - 1;q[block[l]].push_back( node( l, r, i ) );}for( int i = 1;i <= block[N];i ++ )if( ! q[i].empty() )solve( i );for( int i = 1;i <= m;i ++ )printf( "%d\n", ret[i] );return 0;
}