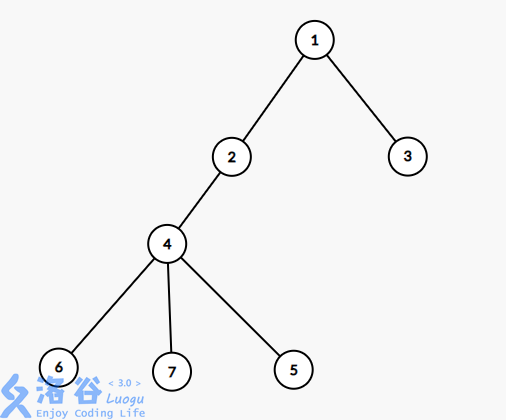
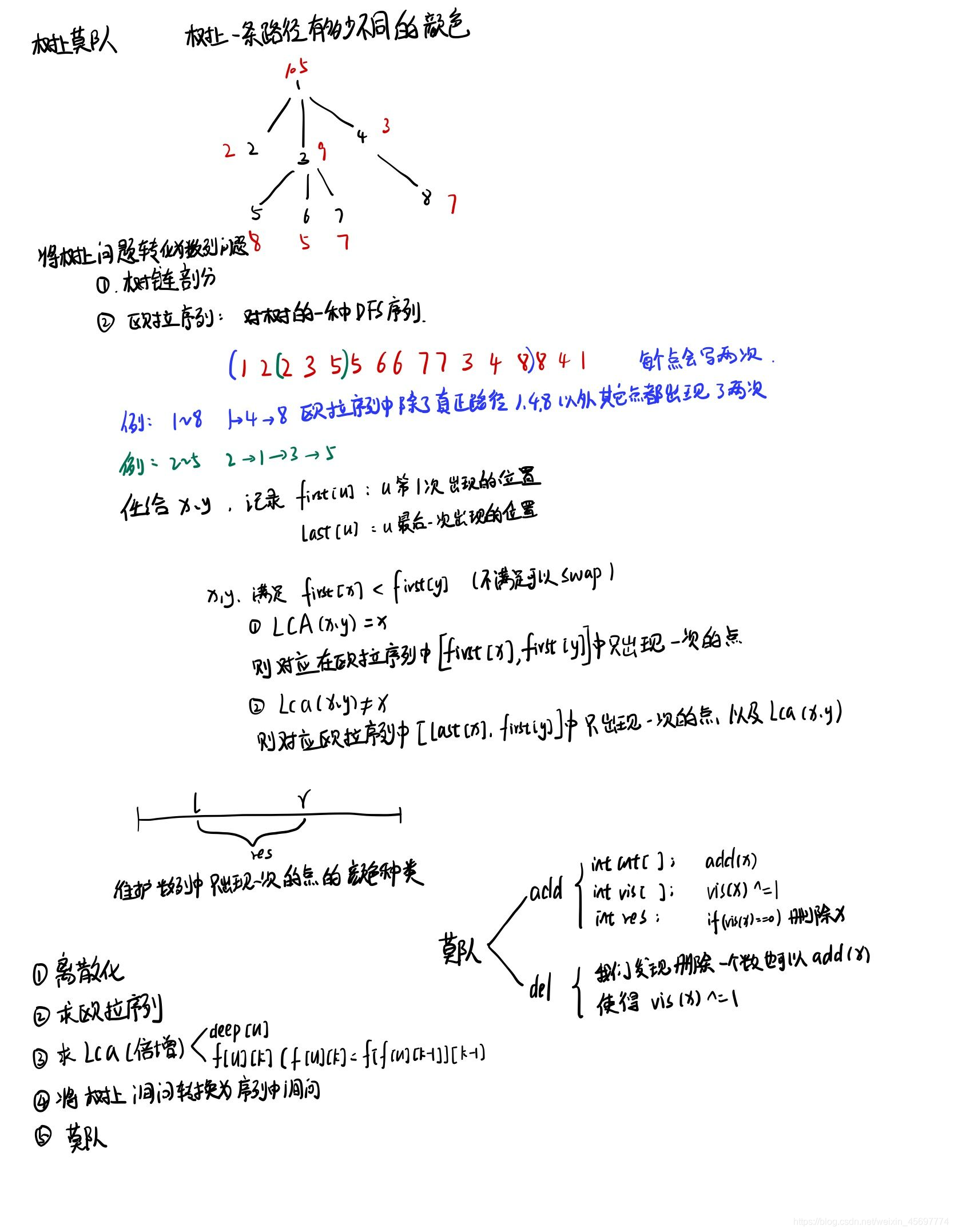
待补：树上莫队，二次离线莫队

关于莫队 其实是个神奇的暴力算法..

通常就是一种处理区间的东西 通过上一次的的左端点和右端点跳来跳去 从而得到这次区间的值

很暴力啊...完全不用思考就能懂的 那么 接下来首先是

普通莫队

排序和移动两点提及一下

关于排序 :

Q1 : 为什么要排序？

A1 : 因为可能两次询问的区间不重叠 如 [1,233] 和 [233,2333] 那多麻烦

Q2 : 那按左端点位置排还是右端点位置排？

A2 : 都是片面的 举个例子 [1,2333] [2,4] [3,2333] [4,6] 这几个如果按左端点排 右端点要跳四千多次 另一个同理

Q3 : 那要怎么排呢？

A3 : 分块排序 同一块中按其中一种排序 不同块中就按另一种排序 然后块的话....自己分个合适的就好 不要一个一块之类就好

然后听说这个的复杂度比较玄学......

关于处理每个询问 :

左右端点同理 这里以左为 Eg :

    如果 原来的 l 在 本次 l 的 左边 说明右侧部分区间无用但上次记录了 于是往右移 删除第 l 个点的影响 然后使 l = l + 1

    如果 原来的 l 在 本次 l 的 右边 说明左侧部分区间有用但上次没记录 于是往左移 增加第 l - 1 个点的影响 并使 l = l - 1

好了下放例题 然后下放代码

#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;
const int MAXN = 100010;
struct bot {int l,r,id;
} s[MAXN];
int ans[MAXN],tot[MAXN],v[MAXN],base,l,r,answ;
inline short cmpto(bot x,bot y) {return x.l/base==y.l/base?x.r<y.r:x.l<y.l;}
inline void del(int p){if (!(--tot[v[p]])) --answ;}
inline void inc(int p){if (++tot[v[p]] == 1) ++answ;}
int main()
{int n,m;scanf("%d%d",&n,&m),base = sqrt(m);for (int a = 1 ; a <= n ; ++ a) scanf("%d",&v[a]);for (int a = 1 ; a <= m ; ++ a) scanf("%d%d",&s[a].l,&s[a].r),s[a].id = a;sort(s + 1,s + m + 1,cmpto);for (int a = 1 ; a <= m ; ++ a){int i = s[a].l,j = s[a].r;while (l < i) del(l++);while (l > i) inc(--l);while (r < j) inc(++r);while (r > j) del(r--);if (answ == j - l + 1) ++ans[s[a].id];}for (int a = 1 ; a <= m ; ++ a)if (ans[a]) printf("Yes\n");else printf("No\n");return 0;
}

然后来看看升级版的 题目戳这里 最后两个点卡莫队

然而事实上略略优化一下 然后 Take a O2 breath 就可以过了

主要还是分块大小需调整 这个优化对玄学算法很有帮助 不过很有碰运气的成分 例如 (下放AC链接)

https://www.luogu.org/record/show?rid=11544517

https://www.luogu.org/record/show?rid=11544631

这第二个的最后一个点是卡着 1000ms 过的......  然后感觉管理看见鄙人过了又要加强数据了 =-=

下放代码

#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;
const int MAXN = 500005;
struct bot {int l,r,id;
} s[MAXN];
int v[MAXN],tot[MAXN << 1],ans[MAXN],l,r,base,answ;
inline short cmp(bot x,bot y) {return x.l/base==y.l/base?x.r<y.r:x.l<y.l;}
inline void del(int p) {if (!(--tot[v[p]])) --answ;}
inline void inc(int p) {if (++tot[v[p]] == 1) ++answ;}
inline int re()
{char q = getchar(); int x = 0;while (q < '0' || q > '9') q = getchar();while ('0' <= q && q <= '9') x = (x << 3) + (x << 1) + q - (3 << 4),q = getchar();return x;
}
int main()
{int n = re();base = n>=2333?2333:n;for (int a = 1 ; a <= n ; ++ a) v[a] = re();int m = re();for (int a = 1 ; a <= m ; ++ a) s[a].l = re(),s[a].r = re(),s[a].id = a;sort(s + 1,s + m + 1,cmp);for (int a = 1 ; a <= m ; ++ a){int i = s[a].l,j = s[a].r;while (l < i) answ -= !(--tot[v[l++]]);while (l > i) answ += ++tot[v[--l]] == 1;while (r < j) answ += ++tot[v[++r]] == 1;while (r > j) answ -= !(--tot[v[r--]]);ans[s[a].id] = answ;}for (int a = 1 ; a <= m ; ++ a) printf("%d\n",ans[a]);return 0;
}

好了话不多说 进入下一块 接下来是

带修莫队

看名字很明显 就是带修改的莫队

哇带修改好强啊 而且听说别称是可持久化莫队？难道还要开20倍空间存版本？

但别忘了我们的莫队是个暴力算法 你再持久也是暴力算 维护啥版本呢

于是 这里的时间就可以理解为 像左右一样的 一个维度就好

用处的话同普通莫队 就是查询区间 但是同时支持了修改区间 (或单点) 的值

没有想法？其实只添加了几行而已！不要以为查询版本很麻烦 其实也就像左右端点一样跳来跳去就好啦

关于排序

同普通莫队的排序 但同样我们可以举出 l 和 r 差不多 但是 版本 (用 e 表示) 每次要跳上千次的反例

所以我们排序还要考虑版本 即 l 和 r 都是 同一块的时候 按版本大小排 然后比较整洁的表示方法是这样的

short cmp(bot x,bot y)
{if (x.l / base != y.l / base) return x.l < y.l;//base是块大小if (x.r / base != y.r / base) return x.r < y.r;return x.edit < y.edit;
}

关于查询之前的版本预处理

我们需要记录第 sizq 次修改的点 和 修改前 修改后的值 再记录第 x 次询问时 修改了几个值就好

可以显然地发现 每次记录询问时 此时已经修改的次数肯定是递增 (可能同) 的 反正不可能减 然而这条并没有什么卵用.....

不过我们处理会方便一点！

修改的要像这样记录 其中 sizr 很显然是记录输入的修改操作的次数

	date[++sizr].ago = cpy[x];date[sizr].nod = x;date[sizr].ure = y;cpy[x] = y;

然后询问同普通莫队 不过要加上一个这个玩意 还有编号肯定不是 1 到 m 了 所以也要用一个数来存询问个数

	//s[a].id = a; 这句改成下一行的s[++sizq].id = sizq;s[sizq].edit = sizr;//上面就是存当前点修改的版本啦

正式关于查询

查询的话嘛 同普通莫队 但在这之前要把版本调到当前查询的版本

同样两个 while 一大于一小于 不多讲 (看代码绝对能懂了) 然后要记住 如果修改的点在区间里面 就要像左右端点加减一样 修改 answ 的值 但如果不在的话 修改 v 数组的值 就好了

哦对了关于 v 数组

就是读入初始值的数组啊 用这个顺便修改 因为左右端点跳的时候是通过 v 数组判定的 所以顺便要修改这个

然后之前预处理存修改的数组 因为要前驱所以也要用到 v 数组 所以建议开一个相同的数组 cpy 然后预处理时修改这个

还要还有 之前左右端点判重不是 ++--tot[v[p]] 嘛 因为查版本修改的数直接是颜色了 为了查询方便一点 改成 ++--tot[p]

其实完全可以在版本修改的子程序里重打一遍的...上面那种办法在外面的话 l++ r-- 之类的还要套上一个 v[ ]

继续关于查询

查询多出来的 while 长这样子

	z = s[a].edit;while (e < z) ++e,ate(date[e].nod,date[e].ure);while (e > z) ate(date[e].nod,date[e].ago),--e;

千万不要写成这样子

	z = s[a].edit;while (e < z) ate(date[++e].nod,date[e].ure);while (e > z) ate(date[e].nod,date[e--].ago);

然后 ate (就是 update 吃货别想歪了) 长这样

void ate(int p,int f)
{if (l <= p && p <= r) del(v[p]),inc(f);v[p] = f;
}

其他和普通莫队差不多了 下放例题 还有代码

#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;
const int MAXN = 50005;
const int MAXM = 1000010;
struct bot {int l,r,edit,id;
} s[MAXN];
struct etion {int nod,ago,ure;
} date[MAXN];
int tot[MAXM],ans[MAXN],v[MAXN],cpy[MAXN],sizq,sizr,base,l,r,e,answ;
void inc(int p) {if (++tot[p] == 1) ++answ;}
void del(int p) {if (!(--tot[p])) --answ;}
void ate(int p,int f)
{if (l <= p && p <= r) del(v[p]),inc(f);v[p] = f;
}
short cmp(bot x,bot y)
{if (x.l / base != y.l / base) return x.l < y.l;if (x.r / base != y.r / base) return x.r < y.r;return x.edit < y.edit;
}
int main()
{char q[4];int n,m,x,y,z;scanf("%d%d",&n,&m);for (int a = 1 ; a <= n ; ++ a) scanf("%d",&v[a]),cpy[a] = v[a];for (int a = 1 ; a <= m ; ++ a){scanf("%s%d%d",q,&x,&y);if (q[0] == 'Q'){s[++sizq].id = sizq;s[sizq].edit = sizr;s[sizq].l = x;s[sizq].r = y;continue;}date[++sizr].ago = cpy[x];date[sizr].nod = x;date[sizr].ure = y;cpy[x] = y;}base = pow(n,2.0 / 3);//那种听说比base = sqrt(n);快诶sort(s + 1,s + sizq + 1,cmp);for (int a = 1 ; a <= sizq ; ++ a){x = s[a].l;y = s[a].r;z = s[a].edit;while (e < z) ate(date[++e].nod,date[e].ure);while (e > z) ate(date[e].nod,date[e--].ago);while (l < x) del(v[l++]);while (l > x) inc(v[--l]);while (r < y) inc(v[++r]);while (r > y) del(v[r--]);ans[s[a].id] = answ;}for (int a = 1 ; a <= sizq ; ++ a) printf("%d\n",ans[a]);return 0;
}