【算法笔记】莫队算法（基础莫队，带修莫队，回滚莫队，树上莫队，二次离线莫队）

整理的算法模板合集： ACM模板

我们首先考虑双指针的暴力法，发现很容易就会被卡成 $O (n m)$ ，这时候我们的莫队出现了，莫队说，我可以像变魔术一样，把 $O (n m)$ 的算法通过一个神奇的排序方式，使得我们最坏的情况下，时间复杂度也会非常优秀： $O(n\sqrt{n})$ 。

莫队算法是一个离线的算法，我们先将所有的询问全部存下来，然后排序。我们的每一个询问都是一个左右区间， $(l, r)$

我们的排序方法为双关键字排序，我们将每个询问的左端点 $l$ 分块。
第一关键字为左端点分块的编号从小到大，第二关键字为右端点的下标从小到大。
在这里插入图片描述

编码时，还可以对排序做一个小优化：奇偶性排序，让奇数块和偶数块的排序相反。例如左端点L都在奇数块，则对R从大到小排序；若L在偶数块，则对R从小到大排序（反过来也可以：奇数块从小到大，偶数块从大到小）。

1. 基础莫队

AcWing 2492. HH的项链
在这里插入图片描述

#include <cstdio>
#include <algorithm>
#include <cstring>
#include <iostream>
#include <cmath>using namespace std;
const int N = 50007, M = 200007, S = 1000007;int n, m;
int w[N];
int block;
int cnt[S];
int ans[M];struct Query{int id, l, r;
}q[M];int get_block(int x){return x / block;//这里是从0开始
}bool cmp(const Query& x, const Query& y){int a = get_block(x.l);int b = get_block(y.l);if(a != b)return a < b;return x.r < y.r;
}void add(int x, int &res){if(cnt[x] == 0)res ++ ;cnt[x] ++ ;
}void del(int x, int &res){cnt[x] -- ;if(cnt[x] == 0)res -- ;
}int main()
{scanf("%d", &n);for(int i = 1; i <= n; ++ i) scanf("%d", &w[i]);scanf("%d", &m);block = sqrt((double)n * n / m);//1488 ms//block = sqrt(n);             //1700 msfor(int i = 0; i < m; ++ i){int l, r;scanf("%d%d", &l, &r);q[i] = {i, l, r};}sort(q, q + m, cmp);for(int k = 0, i = 0, j = 1, res = 0; k < m; ++ k){int id = q[k].id, l = q[k].l, r = q[k].r;while(i < r)add(w[ ++ i], res);while(i > r)del(w[i -- ], res);while(j < l)del(w[j ++ ], res);while(j > l)add(w[ -- j], res);//注意这里的细节，自己模拟一遍ans[id] = res;}for(int i = 0; i < m; ++ i)printf("%d\n", ans[i]);return 0;
}

玄学优化版，成功卡过了洛谷上的这道题

#include <cstdio>
#include <algorithm>
#include <cstring>
#include <iostream>
#include <cmath>using namespace std;
const int N = 1000007, M = 1000007, S = 1000007;int n, m;
int w[N];
int block;
int cnt[S];
int ans[M];inline int read()
{int x = 0, f = 1;char ch = getchar();while(ch > '9' || ch < '0'){if(ch == '-')f = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){x = x * 10 + ch - '0';ch = getchar();}return x * f;
}inline void write(int res){if(res<0){putchar('-');res=-res;}if(res>9)write(res/10);putchar(res%10+'0');
}struct Query{int id, l, r;
}q[M];inline int get_block(int x){return x / 2000;//这里是从0开始
}bool cmp(const Query& x, const Query& y){int a = get_block(x.l);int b = get_block(y.l);//int a = x.l / block, b = y.l / block;if(a != b)return a < b;if(a & 1)return x.r < y.r;return x.r > y.r;
}inline void add(int x, int &res){if(cnt[x] == 0)res ++ ;cnt[x] ++ ;
}inline void del(int x, int &res){cnt[x] -- ;if(cnt[x] == 0)res -- ;
}int main()
{n = read();for(register int i = 1; i <= n; ++ i) w[i] = read();m = read();block = sqrt((double)n * n / m);//1488 ms//block = sqrt(n);             //1700 ms//block = 2000;for(register int i = 0; i < m; ++ i){int l = read(), r = read();q[i] = {i, l, r};}sort(q, q + m, cmp);for(register int k = 0, i = 0, j = 1, res = 0; k < m; ++ k){int id = q[k].id, l = q[k].l, r = q[k].r;while(i < r)add(w[ ++ i], res);while(i > r)del(w[i -- ], res);while(j < l)del(w[j ++ ], res);while(j > l)add(w[ -- j], res);//注意这里的细节，自己模拟一遍/*while(i < r)res += ++ cnt[w[ ++ i]] == 1;while(i > r)res -= -- cnt[w[i -- ]] == 0;while(j < l)res -= -- cnt[w[j ++ ]] == 0;while(j > l)res += ++ cnt[w[ -- j]] == 1;
*/ans[id] = res;}for(register int i = 0; i < m; ++ i)write(ans[i]), puts("");return 0;
}

2. 带修莫队

AcWing 2521. 数颜色
在这里插入图片描述

我发现直接把块的大小开成一个常数跑的最快…

//#pragma GCC optimize(2)
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <iostream>
#include <cmath>
using namespace std;const int N = 1000007, M = 1000007, S = 1000007;inline int read()
{int x = 0, f = 1;char ch = getchar();while(ch > '9' || ch < '0'){if(ch == '-')f = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){x = x * 10 + ch - '0';ch = getchar();}return x * f;
}inline void write(int res){if(res<0){putchar('-');res=-res;}if(res>9)write(res/10);putchar(res%10+'0');
}int n, m;
int block = 2589;//n ^ (2 / 3)
int w[N];
int cnt[S];
int ans[N];
int bi[N];
struct Query{int id, l, r, t;
}q[M];struct Modify{int pos, col, lst;
}c[M];bool cmp(const Query &a, const Query &b){int al = bi[a.l], ar = bi[a.r];int bl = bi[b.l], br = bi[b.r];if(al != bl)return a.l < b.l;if(ar != br)return a.r < b.r;return a.t < b.t;
}void add(int x, int& res){if(cnt[x] == 0)res ++ ;cnt[x] ++ ;
}void del(int x, int& res){cnt[x] -- ;if(cnt[x] == 0)res -- ;
}int main()
{n = read(), m = read();for(register int i = 1; i <= n; ++ i) w[i] = read();int mq = 0, mc = 0;for(register int i = 1; i <= m; ++ i){char op[2];int l, r;scanf("%s", op);l = read(), r = read();if(op[0] == 'Q'){q[ ++ mq] = (Query){mq, l, r, mc};}else {c[ ++ mc] = (Modify){l, r};}}//这里block一定要加1，可能出现0的情况导致除0发生浮点错误//block=ceil(exp((log(n)+log(mc))/3));//分块大小//block = cbrt(n * mc);//block = pow(n * n, 1.0 / 3);//block = pow(n, 2.0 / 3);for(int i = 1; i <= n; ++ i){bi[i] = (i - 1) / block;}sort(q + 1, q + 1 + mq, cmp);for(register int k = 1, i = 0, j = 1, t = 0, res = 0; k <= mq; ++ k){int id = q[k].id, l = q[k].l, r = q[k].r, tim = q[k].t;//先处理x轴/*while(i < r)add(w[ ++ i], res);while(i > r)del(w[i -- ], res);while(j < l)del(w[j ++ ], res);while(j > l)add(w[ -- j], res);*/while(i < r)res += ++ cnt[w[ ++ i]] == 1;while(i > r)res -= -- cnt[w[i -- ]] == 0;while(j < l)res -= -- cnt[w[j ++ ]] == 0;while(j > l)res += ++ cnt[w[ -- j]] == 1;//再处理y轴while(t < tim){t ++ ;if(c[t].pos >= j && c[t].pos <= i){del(w[c[t].pos], res);add(c[t].col, res);//res -= !--cnt[w[c[t].pos]] - !cnt[c[t].col]++;}swap(w[c[t].pos], c[t].col);}while(t > tim){if(c[t].pos >= j && c[t].pos <= i){del(w[c[t].pos], res);add(c[t].col, res);//res -= !--cnt[w[c[t].pos]] - !cnt[c[t].col]++;}swap(w[c[t].pos], c[t].col);t -- ;}ans[id] = res;}for(register int i = 1; i <= mq; ++ i)write(ans[i]), puts("");return 0;
}

3. 回滚莫队

AcWing 2523. 历史研究

在这里插入图片描述

左指针j，右指针i。

对于块外的情况，左端点一定是在块内的，如果有的询问的右端点是在块外，我们把i右定在right，j左端点定在right+1，我们i右端点一定只会一直向右走，因为我们是按照右端点升序排序的，块外的时候j往左走到实际位置左端点，只有增加操作，维护答案。

还是要删除的，但是删除的时候只需要维护cnt即可，res已经更新过了。

注意res只是当前块的右端点到中间的res，但是我们的答案是整个区间，所以我们备份一下中间到右端的res，往左走更新res，更新答案以后res回档为备份，相当于一个 $O (1)$ 删除操作，我们每次更新所有左端点在一个块的好多个询问区间，所以每次cnt需要每次清零。

#include <cstdio>
#include <algorithm>
#include <cstring>
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
typedef long long ll;
const int N = 200007;int read()
{int x = 0, f = 1;char ch = getchar();while(ch > '9' || ch < '0') {if(ch == '-')f = -1;ch = getchar();}while(ch <= '9' && ch >= '0') {x = x * 10 + ch - '0';ch = getchar();}return x * f;
}int n, m;
int bi[N];
int v[N];
int block;
ll ans[N];struct Query
{int id, l, r;
}q[N];bool cmp(const Query& x, const Query& y) {int a = bi[x.l], b = bi[y.l];if(a != b) return a < b;return x.r < y.r;
}vector<int>nums;
int cnt[N];int get_block(int x)
{return x / block;
}void add(int x, ll& res)
{cnt[x] ++ ;res = max(res, (ll)cnt[x] * nums[x]);
}int main()
{n = read(), m = read();block = sqrt(n);for(int i = 1 ; i <= n; ++ i) {v[i] = read();nums.push_back(v[i]);bi[i] = i / block;}sort(nums.begin(), nums.end());for(int i = 1; i <= n; ++ i) {v[i] = lower_bound(nums.begin(), nums.end(), v[i]) - nums.begin();}for(int i = 0; i < m; ++ i) {int l = read(), r = read();q[i] = {i, l, r};}sort(q, q + m, cmp);for(int x = 0; x < m;) {//先找同一个块里的左右询问区间左x右y;int y = x;while(y < m && bi[q[y].l] == bi[q[x].l]) y ++ ;int right = bi[q[x].l] * block + block - 1; //当前块的右界while(x < y && q[x].r <= right) {ll res = 0;int id = q[x].id, l = q[x].l, r = q[x].r;for(int k = l; k <= r; ++ k)//O(sqrt(n))add(v[k], res);ans[id] = res;for(int k = l; k <= r; ++ k)cnt[v[k]] -- ;x ++ ;}ll res = 0;int i = right, j = i + 1;//j是左指针i是右指针while(x < y){int id = q[x].id, l = q[x].l, r = q[x].r;while(i < r) add(v[ ++ i], res);ll backup = res;//res只是当前块的右端点到右指针的答案，所以要备份while(j > l) add(v[ -- j], res);//这个询问区间的左端点一定在左块内部，我们就是这么排序的ans[id] = res;while(j < right + 1) cnt[v[j ++ ]] -- ;res = backup;x ++ ;}memset(cnt, 0, sizeof cnt);}for(int i = 0; i < m; ++ i)printf("%lld\n", ans[i]);return 0;
}

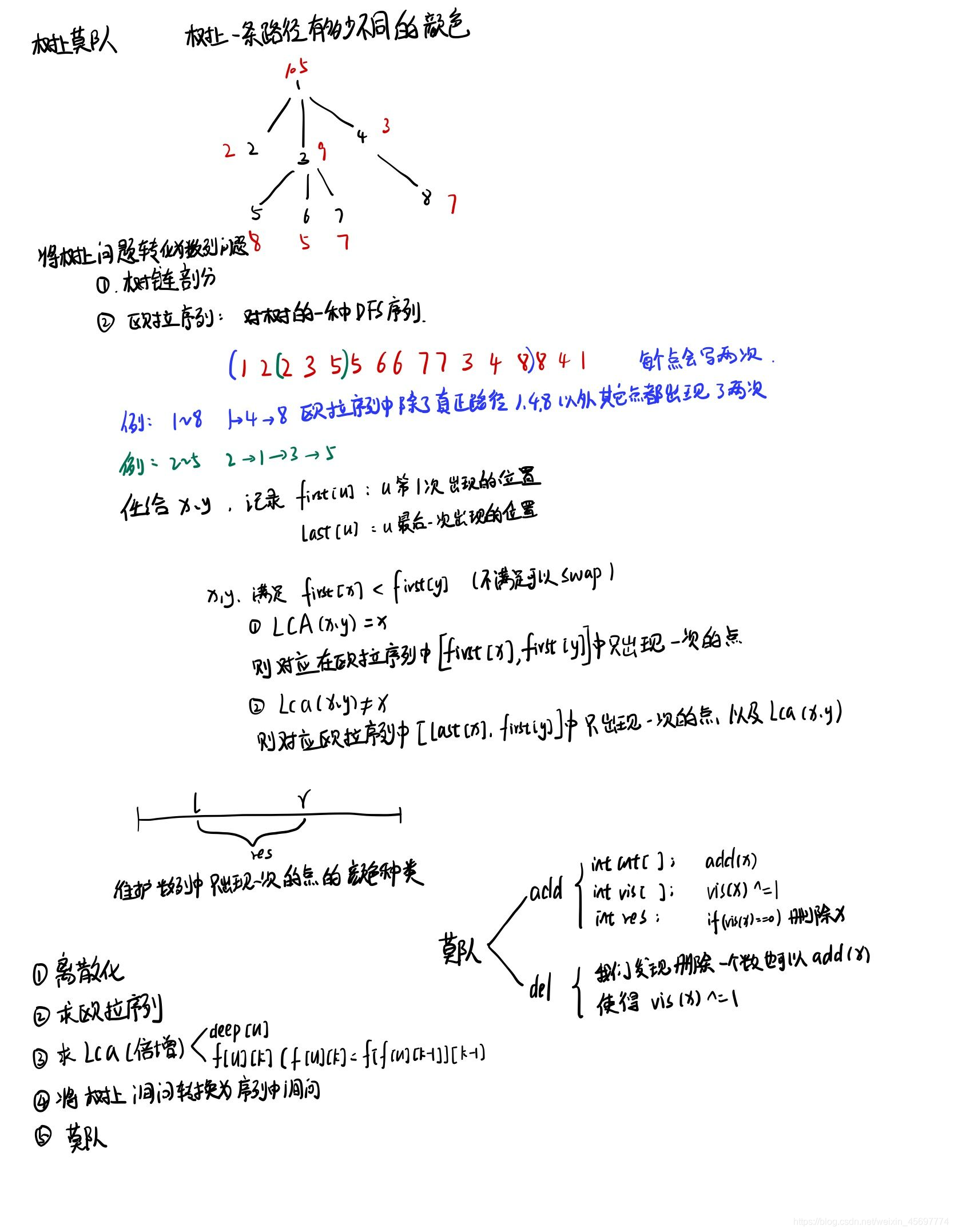
4. 树上莫队

AcWing 2534. 树上计数2

在这里插入图片描述

#include <cstdio>
#include <algorithm>
#include <cstring>
#include <iostream>
#include <vector>
#include <cmath>
//如果顺序有关系，涉及修改，需要用树链剖分
using namespace std;
//不涉及修改，没有顺序关系的可以用欧拉序列
const int N = 500007, M = 500007, INF = 0x3f3f3f3f;
int n, m;
int cnt[N], vis[N];
vector<int>v;
int f[N][20], dep[N];
int head[N], ver[M], nex[M], tot;
int w[M];
int seq[N], top, first[N], last[N];
int block;
int ans[N];void add_edge(int x, int y)
{ver[tot] = y;nex[tot] = head[x];head[x] = tot ++ ;
}struct Query{int id, l, r, p;
}q[N];int get_block(int x)
{return x / block;
}bool cmp(Query &a, Query &b)
{int x = get_block(a.l);int y = get_block(b.l);if(x != y)return x < y;return a.r < b.r;
}void dfs(int x, int fa){seq[ ++ top] = x;first[x] = top;for(int i = head[x]; ~i; i = nex[i]){int y = ver[i];if(y == fa) continue;dfs(y, x);}seq[ ++ top] = x;last[x] = top;
}int que[N];void bfs()
{memset(dep, 0x3f, sizeof dep);int hh = 0, tt = 0;que[0] = 1;dep[0] = 0, dep[1] = 1;while(hh <= tt){int x = que[hh ++ ];if(hh == N) hh = 0;for(int i = head[x]; ~i; i = nex[i]){int y = ver[i];if(dep[y] > dep[x] + 1){dep[y] = dep[x] + 1;f[y][0] = x;for(int k = 1; k <= 15; ++ k){f[y][k] = f[f[y][k - 1]][k - 1];}que[ ++ tt] = y;if(tt == N) tt = 0;}}}
}int lca(int x, int y)
{if(dep[x] < dep[y]) swap(x, y);for(int k = 15; k >= 0; -- k){if(dep[f[x][k]] >= dep[y]){x = f[x][k];}}if(x == y) return x;for(int k = 15; k >= 0; -- k){if(f[x][k] != f[y][k]){x = f[x][k];y = f[y][k];}}return f[x][0];
}void add(int x, int &res)
{//!欧拉序列中出现两次就不是路径上的点了!要删掉//要删掉的点一定是只出现一次的，添加的时候add一次，删除的时候add一次，两次即为删除vis[x] ^= 1;//需要的是点的编号if(vis[x] == 0){cnt[w[x]] -- ;//需要的是点的权值（离散化过了）if(cnt[w[x]] == 0) res -- ;}else {cnt[w[x]] ++ ;if(cnt[w[x]] == 1) res ++ ;}
}int main()
{scanf("%d%d", &n, &m);for(int i = 1; i <= n; ++ i){scanf("%d", &w[i]);v.push_back(w[i]);}sort(v.begin(), v.end());v.erase(unique(v.begin(), v.end()), v.end());for(int i = 1; i <= n; ++ i){w[i] = lower_bound(v.begin(), v.end(), w[i]) - v.begin();}memset(head, -1, sizeof head);for(int i = 1; i <= n - 1; ++ i){int x, y;scanf("%d%d", &x, &y);add_edge(x, y);add_edge(y, x);}dfs(1, -1);//得到欧拉序列bfs();//lca预处理for(int i = 0; i < m; ++ i){int a, b;scanf("%d%d", &a, &b);//a,b是树上的点//first[a], first[b], last[a], last[b]才是数列上的点，也是我们莫队要处理的点if(first[a] > first[b]) swap(a, b);int p = lca(a, b);if(a == p)q[i] = {i, first[a], first[b]};else q[i] = {i, last[a], first[b], p}; }block = sqrt(top);//这里应该是欧拉序列里的点的个数sort(q, q + m, cmp);//右指针i左指针j, 右指针先冲左指针跟上//左指针在1，右指针在0，初始状态形成一个空集for(int k = 0, i = 0, j = 1, res = 0; k < m; ++ k){int l = q[k].l, r = q[k].r, id = q[k].id, p = q[k].p;//这里走的应该是欧拉序列里的点了while(i < r) add(seq[ ++ i], res);//addwhile(i > r) add(seq[i -- ], res);//delwhile(j < l) add(seq[j ++ ], res);//delwhile(j > l) add(seq[ -- j], res);//addif(p) add(p, res);ans[id] = res;if(p) add(p, res);//最后一定要删除p，因为它不属于 i 到 i 这一连续序列中}for(int i = 0; i < m; ++ i)printf("%d\n", ans[i]);return 0;
}