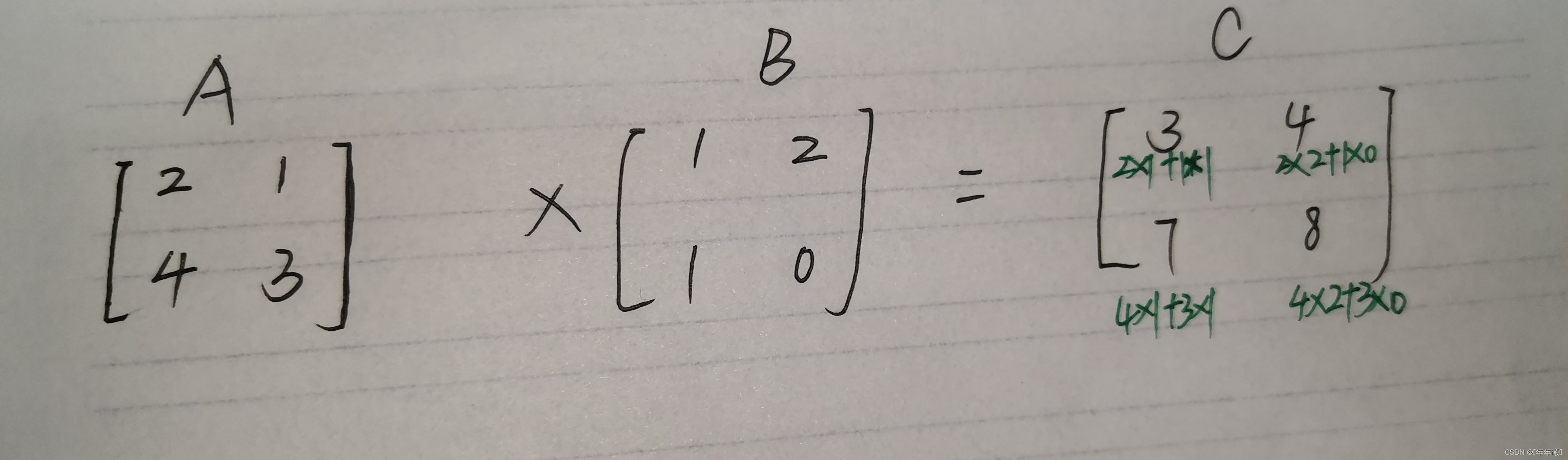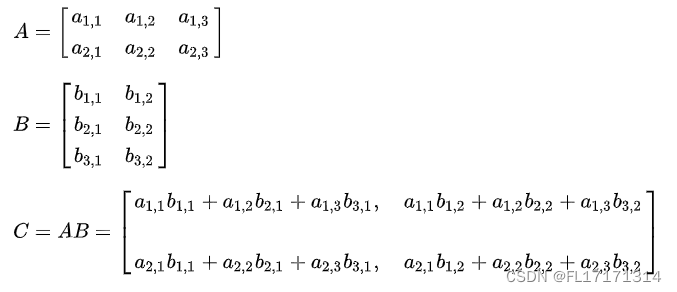之前介绍了C语言用代数余子式求行列式
本次开始介绍如何用公式法对矩阵求逆,并用C语言将其实现。
之前程序有点小bug,已于2022年11月29日修改。
更新:
伴随法只适合求低阶矩阵的逆,对于相对高阶(20维以上)对矩阵求逆用高斯法求解效率更高,此外本文中使用了_msize函数用于判断内存维数,但该函数只适合winodows系统,Linux和Mac系统无法使用(笔者也是在用了Mac系统后才发现),对于上述两个问题,您应该可以在:C语言求矩阵的逆(高斯法)得到满意的答案。
如果矩阵接近奇异值,求逆的数值将不稳定,那么使用C语言LU分解法求逆将会得到更好的效果。
目录
数学原理
矩阵求逆的公式
数乘矩阵
程序设计
整体代码
求行列式的值(Det、Cof)
求伴随矩阵(FindCof)
求逆矩阵的主函数(matrix_inver)
测试
数学原理
矩阵求逆的方法有很多种,本次主要介绍如何利用公式法求解。
矩阵求逆的公式
其中,为A的行列式的值,
为矩阵A的伴随矩阵。
伴随矩阵的表达方式为:
其中,为代数余子式,代数余子式
与余子式
的关系为:
是矩阵A去掉i行j列,剩下元素重新组成的新矩阵 。
数乘矩阵
假设矩阵A为:
如果一个数b乘以一个矩阵A,那么A中的每一个元素都要乘以b,其表示如下:
程序设计
为了后面方便调试,先利用malloc函数创建一个矩阵,并为其赋值。关于malloc函数有不理解的可以参考之前写的C语言动态内存管理。
malloc使用的基本方式:
- void* malloc (size_t size);
- void free (void* ptr);
- size是指定的开辟内存的大小,单位是字节
- size_t的无符号整型则限制程序员误操作开辟负字节的空间
- 如果开辟成功,malloc会返回一个void*类型的指针
- 如果开辟失败,则返回的是空指针,所以在malloc之后需要对指针进行检查
- 当malloc的东西不再使用时,需要free对其进行释放,否则会造成内存泄漏
- malloc和free均需要包含头文件<stdlib.h>
//创建n维矩阵空间,并初始化
double** test1(int n)
{double** arr = (double**)malloc(sizeof(double*) * n);int i, j;if (arr != NULL){for (i = 0; i < n; i++){arr[i] = (double*)malloc(sizeof(double) * n);}//为矩阵赋值if (*arr != NULL){for (i = 0; i < n; i++){for (j = 0; j < n; j++){arr[i][j] = pow(i, j);}}}}return arr;
}其中:
- double** arr = (double**)malloc(sizeof(double*) * n);表示开辟n个double*类型的空间,将其地址赋给arr
- 然后再开辟n个double类型的空间,将其地址赋给double**中每个double*
- 配合下图更好理解

整体代码
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<math.h>
#include<malloc.h>
#include<string.h>#define MatMax 20//函数声明
double Det(const double arr[MatMax][MatMax], int n);
double Cof(const double arr[MatMax][MatMax], int i, int n);
void FindCof(double arr[MatMax][MatMax], double arr2[MatMax][MatMax], int i, int j, int n);
double** matrix_inver(double** arr);//计算行列式
double Det(const double arr[MatMax][MatMax], int n)
{assert(n > 0);double sum = 0;int i = 0;if (n == 1)//1阶行列式直接得出结果{sum = arr[0][0];}else if (n == 2){sum = arr[0][0] * arr[1][1] - arr[0][1] * arr[1][0];//杀戮法求解}else if (n == 3){sum = arr[0][0] * arr[1][1] * arr[2][2]+ arr[0][1] * arr[1][2] * arr[2][0]+ arr[1][0] * arr[2][1] * arr[0][2]- arr[0][2] * arr[1][1] * arr[2][0]- arr[0][1] * arr[1][0] * arr[2][2]- arr[1][2] * arr[2][1] * arr[0][0];//划线法求解}else{for (i = 0; i < n; i++)//按第一行展开{if (arr[0][i] != 0)//展开项不为0才计算{sum += ((int)pow(-1, i + 0)) * arr[0][i] * (Cof(arr, i, n));//2阶以上继续递归 }elsesum += 0;//展开项为0}}return sum;
}
//找到余子式
double Cof(const double arr[MatMax][MatMax], int i, int n)
{assert(n > 0);int k = 0;int j = 0;double arr2[MatMax][MatMax] = { 0 };for (k = 0; k < n - 1; k++)//去除0行i列,剩下的组成新的矩阵{for (j = 0; j < n - 1; j++){if (j < i){arr2[k][j] = arr[k + 1][j];}else{arr2[k][j] = arr[k + 1][j + 1];}}}return Det(arr2, n - 1);
}
//找到去掉i行j列的余子式
void FindCof(double arr[MatMax][MatMax], double arr2[MatMax][MatMax], int i, int j, int n)
{int m = 0;int k = 0;for (m = 0; m < n - 1; m++){for (k = 0; k < n - 1; k++){if (k < j){if (m < i){arr2[m][k] = arr[m][k];}else{arr2[m][k] = arr[m + 1][k];}}else{if (m < i){arr2[m][k] = arr[m][k + 1];}else{arr2[m][k] = arr[m + 1][k + 1];}}}}
}//计算逆的主函数
double** matrix_inver(double** arr)
{int i, j, n;double** res=NULL;n = (int)_msize(arr) / (int)sizeof(double*);res = (double**)malloc(sizeof(double*) * n);if (res == NULL)exit(-1);for (i = 0; i < n; i++){res[i] = (double*)malloc(sizeof(double) * n);memset(res[i], 0, sizeof(double) * n);}double tmp[MatMax][MatMax] = { 0 };//保护arr,将arr指向内存的数据拷贝到tmp二维数组中for (i = 0; i < n; i++){memcpy(tmp[i],arr[i],sizeof(double) * n);}double a = 1.0 / (Det(tmp, n));for (i = 0; i < n; i++){for (j = 0; j < n; j++){double tmp2[MatMax][MatMax] = { 0 };FindCof(tmp, tmp2, j, i, n);//求转置后的伴随double b = pow(-1, i + j) * Det(tmp2, n - 1);res[i][j] = a * b;}}return res;
}接下来针对上述代码进行讲解
求行列式的值(Det、Cof)
通过观察发现,利用公式法求矩阵的逆离不开求行列式的值。我们创建两个函数Det和Cof2
利用代数余子式的方法求解行列式:
Det:求解行列式的主函数,判断行列式的维数,如果维数大于3则进行代数余子式计算,按第一行展开,将其传给Cof函数;如果小于等于3则直接求解,避免过度递归。
Cof:求余子式,将新的余子式传给Det函数。
行列式的计算在这篇博客中C语言计算行列式
求伴随矩阵(FindCof)
该函数与cof函数类似,都是求余子式的,区别在于:
- FindCoi是找到去掉第i行第j列的余子式;Cof函数固定从第1行第j列
- FindCof函数不参与递归,只要找到余子式即可
其中:
- if部分是用来判断组成新的行列式的位置
求逆矩阵的主函数(matrix_inver)
对照之前的公式,对n维的方阵,其伴随矩阵需要求解n*n个代数余子式,利用两个for循环逐行逐列进行处理。
主要思想:
- 计算行列式的值a,计算1/a
- 从i行j列开始,求代数余子式,并将求得的余子式部分传给Det函数,计算其行列式的值b
- 计算a*b,并赋值
主函数中:
- n = (int)_msize(arr) / (int)sizeof(double*);求矩阵的维数,_msize是库函数,需要包含头文件:<malloc.h>求其指针指向地址的内存大小,单位是字节;对照res开辟内存的过程,即可明白其计算原理。
- memcpy(tmp[i],arr[i],sizeof(double) * n);进行内存拷贝,将动态内存中数据拷贝到二维数组中。有两层意义:一:防止递归中造成内存泄漏;二:保护原矩阵
测试
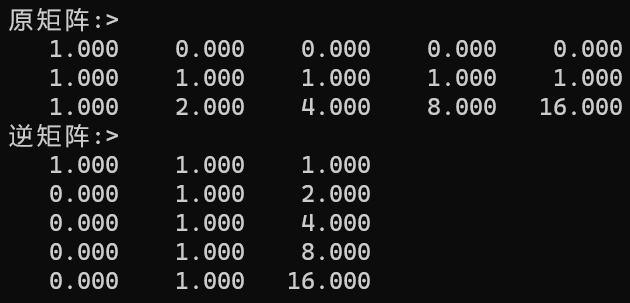
int main()
{int n = 5;double** arr = test1(n);printf("原矩阵:>\n");print(arr);double** res = matrix_inver(arr);printf("逆矩阵:>\n");print(res);return 0;
}其中:
- test1是上述创建矩阵的函数
- print是用来打印矩阵的函数,代码如下:
//打印矩阵
void print(double** arr)
{putchar('\n');int i, j, row, col;row = (int)_msize(arr) / (int)sizeof(double*);//判断行数col = (int)_msize(*arr) / (int)sizeof(double);//判断列数for (i = 0; i < row; i++){for (j = 0; j < col; j++){printf("%10.5lf ", arr[i][j]);}putchar('\n');}putchar('\n');
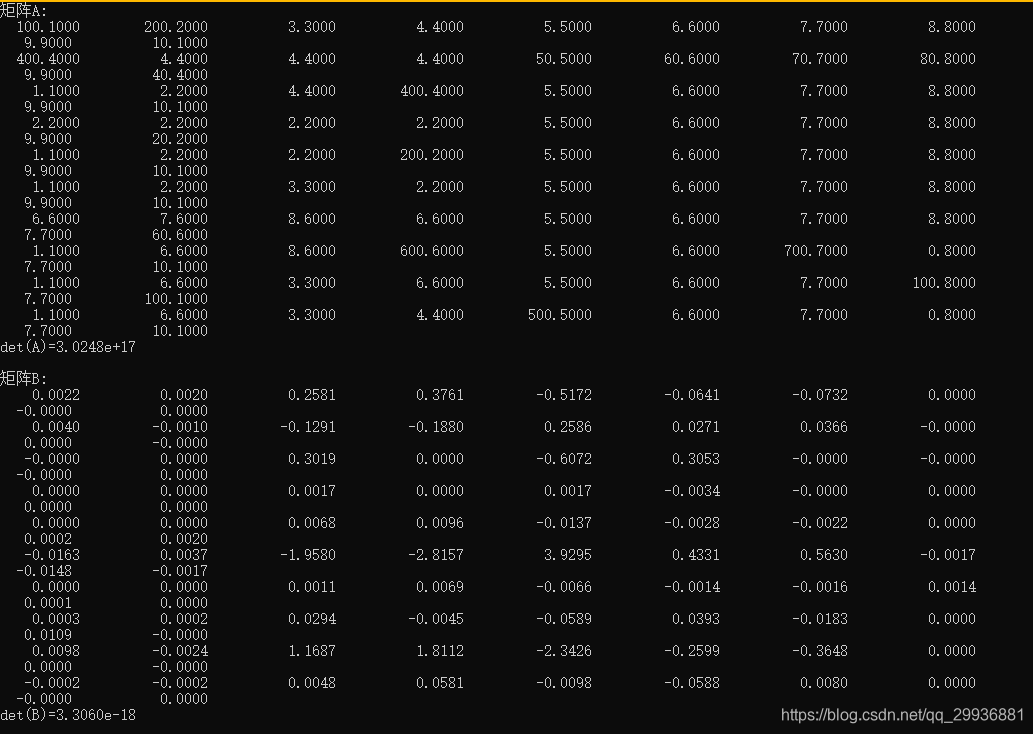
}测试结果如下:
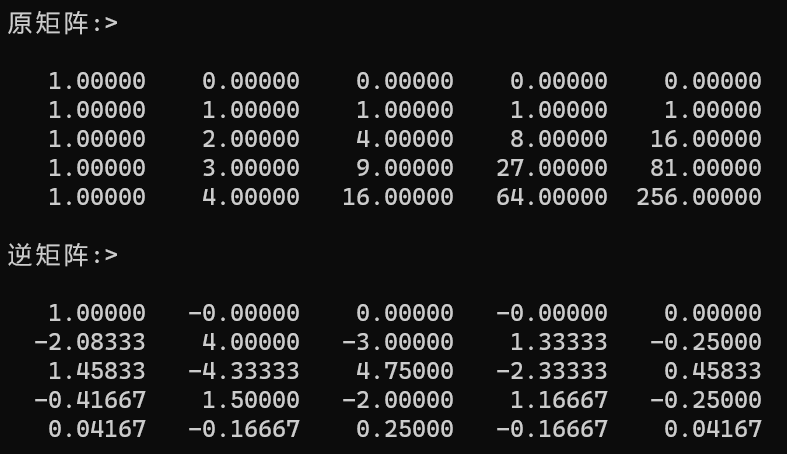
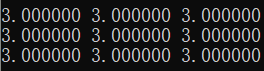
与matlab计算的结果进行比对:

如果矩阵治亏,则会输出:

因为公式法涉及到递归,因此无法计算高维逆矩阵,想要保证精度和效率,可以尝试利用LU分解法进行矩阵求逆,这也是目前大多数计算机在处理高维矩阵时的策略。