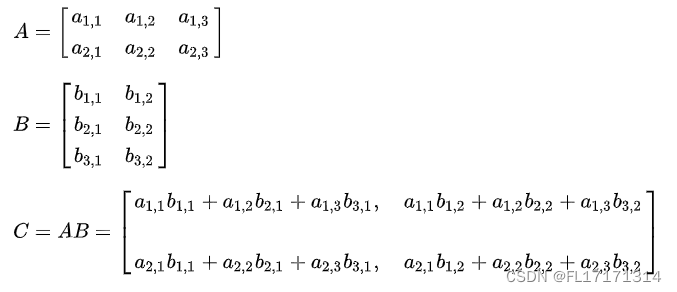目录
1.转置矩阵(普通矩阵)
2.转置矩阵(稀疏矩阵)
(1)稀疏矩阵
(2)稀疏矩阵的压缩存储方式
(3)理论运算方法
1.转置矩阵(普通矩阵)
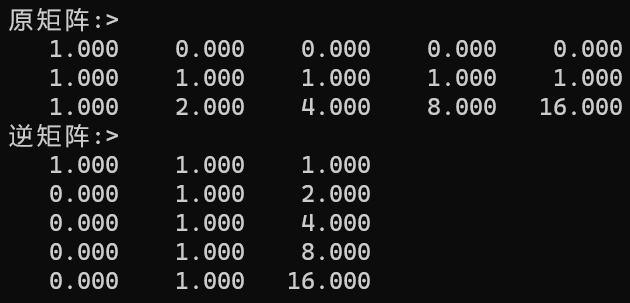
矩阵的转置:根据主对角元素作为对称轴进行元素的互换。转置运算是一种最简单的矩阵运算。对一个mxn的矩阵M进行转置得到矩阵T(nxm),且T(i,j)=M(j,i),1<=i<=n,1<=j<=m.
注:虽然矩阵的转置非常的简单,但是对于其在计算机上的时间复杂度也是做了很多的优化,特别是对稀疏矩阵的转置,因为稀疏矩阵的存储方式不是直接使用nxn的方式进行存储的,而是采用其他的方式:如三元组等。

#include<stdlib.h>
#include<stdio.h>#define Mat_n 5typedef int ElemType;int M[Mat_n][Mat_n];
//矩阵的转置
void TransposeMatrix(int N[Mat_n][Mat_n],int n,int m){for(int col=1;col<=m;col++){for(int row=1;row<=n;row++){M[col][row]=N[row][col];}}
} int main(){int n,m; int N[Mat_n][Mat_n];printf("请输入矩阵(方阵)行和列: ");scanf("%d %d",&n,&m);//初始化for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){N[i][j]=M[i][j]=0; }}printf("请输入矩阵(方阵):\n");for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){scanf("%d",&N[i][j]); }}TransposeMatrix(N,n,m);for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){printf("%d ",M[i][j]);}printf("\n");}return 0;
}/*
4 4
1 2 0 3
5 6 3 8
12 23 45 67
9 5 3 5
*/2.转置矩阵(稀疏矩阵)
(1)稀疏矩阵
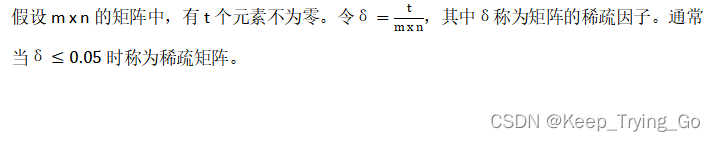
(2)稀疏矩阵的压缩存储方式
由于是稀疏矩阵,所以只需要存储非零元即可,非零元的位置为(i,j),所以采用三元组的形式(i,j,aij)唯一确定矩阵A的非零元。
比如:((1,2,2),(1,3,9),(3,1,3),(3,6,4),(4,3,2),(5,2,8),(6,1,5),(6,4,7))

(3)理论运算方法
假设M矩阵的三元组形式如下:
| 行 | 列 | 元素 |
| 1 | 2 | 12 |
| 1 | 3 | 9 |
| 3 | 1 | -3 |
| 3 | 6 | 14 |
| 4 | 3 | 24 |
| 5 | 2 | 18 |
| 6 | 1 | 15 |
| 6 | 1 | -7 |
转置之后的T矩阵三元组如下:
| 行 | 列 | 元素 |
| 1 | 3 | -1 |
| 1 | 6 | 15 |
| 2 | 1 | 12 |
| 2 | 5 | 18 |
| 2 | 1 | 9 |
| 2 | 4 | 24 |
| 4 | 6 | -7 |
| 6 | 3 | 14 |
步骤:
第一步:将矩阵的行列值进行互换;
第二步:将每个元组中的i和j值进行调换;
第三步:重排三元组之间的次序即可实现矩阵的转置;
而对于第三步的具体实现步骤:
方法一:
按照T.data中的三元组的次序依次在M.data中找到相应的三元组进行转置。也就是说对其M.data中的三元组表进行扫描一遍(从第一行到最后一行),由于M.data是以行序为主序来存放每个非零元的,所以也可以得到T.data应有的次序。
#include<stdlib.h>
#include<stdio.h>#define MAXSIZE 10typedef int ElemType;typedef struct {int i,j;ElemType e;
}Triple;typedef struct {Triple data[MAXSIZE];int mu,nu,tu;//矩阵的行,列和非零元个数
}TSMatrix; void TransposeSMatrix(TSMatrix M,TSMatrix&T){//矩阵的行列互换 T.mu=M.nu;T.nu=M.mu;T.tu=M.tu;if(T.tu){int q=1;for(int col=1;col<=M.nu;col++){for(int p=1;p<=M.tu;p++){if(M.data[p].j==col){T.data[q].i=M.data[p].j;T.data[q].j=M.data[p].i;T.data[q].e=M.data[p].e;q++;}}}}
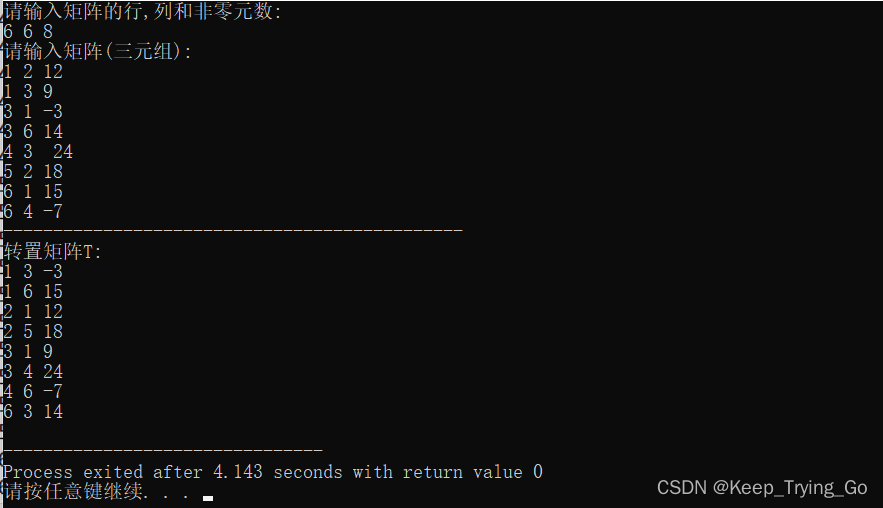
}int main(){TSMatrix M,T;printf("请输入矩阵的行,列和非零元数: \n");scanf("%d %d %d",&M.mu,&M.nu,&M.tu);printf("请输入矩阵(三元组): \n");for(int i=1;i<=M.tu;i++){scanf("%d %d %d",&M.data[i].i,&M.data[i].j,&M.data[i].e);}printf("----------------------------------------------\n");TransposeSMatrix(M,T);printf("转置矩阵T: \n");for(int i=1;i<=T.tu;i++){printf("%d %d %d\n",T.data[i].i,T.data[i].j,T.data[i].e);}return 0;
}
/*
6 6 81 2 12
1 3 9
3 1 -3
3 6 14
4 3 24
5 2 18
6 1 15
6 4 -7
*/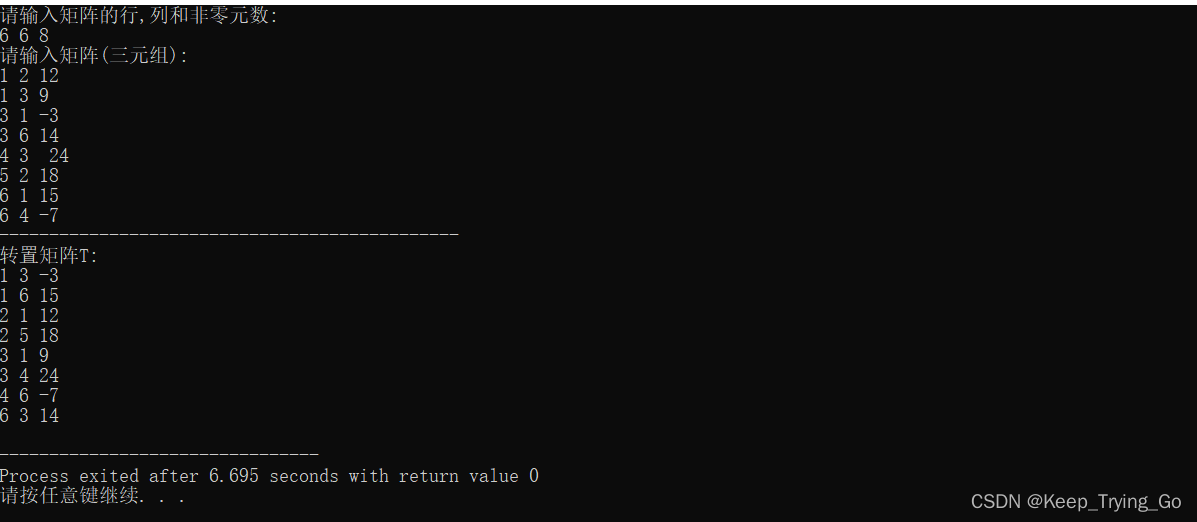
注:但是方法一从时间复杂度上来说:O(nu x tu),所以和非零元的个数是成正比的;普通的矩阵的转置时间复杂度为O(mu x nu);但是对于方法一来说,当tu的数量级和nu x mu相同时,就会出现时间复杂度为O(mu x nu x nu),所以这个时候比普通的方法还要耗时。因此方法二对其进行了改进。
方法二:
假设:如果能够预先确定矩阵M中的每一列(也就是转置之后的矩阵中的每一行)的第一个非零元在T.data中的应有位置,那么在对M.data中的三元组依次做转置时,便可直接放到T.data中恰当的位置。
为了提前确定位置,首先需要设置两个数组变量:num和cpot。
其中num[col]表示矩阵M中的第col列中非零元的个数,cpot[col]表示M中第col列的第一个非零元在T.data中的恰当位置。
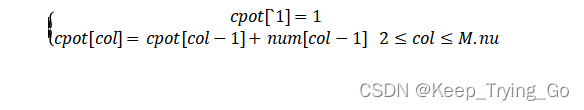
| col | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| num[co] | 2 | 2 | 2 | 1 | 0 | 1 | 0 |
| cpot[col] | 1 | 3 | 5 | 7 | 8 | 8 | 9 |
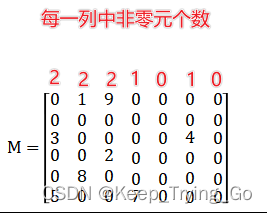
num[co]更加形象的计算方式:

#include<stdlib.h>
#include<stdio.h>#define MAXSIZE 10const int maxn=100;typedef int ElemType;typedef struct {int i,j;ElemType e;
}Triple;typedef struct {Triple data[MAXSIZE];int mu,nu,tu;//矩阵的行,列和非零元个数
}TSMatrix; void TransposeSMatrix_1(TSMatrix M,TSMatrix&T){//矩阵的行列互换 T.mu=M.nu;T.nu=M.mu;T.tu=M.tu;int num[100];int cpot[100];if(T.tu){//初始化for(int col=1;col<=M.nu;col++){num[col]=0;}for(int t=1;t<=M.tu;t++){++num[M.data[t].j];}cpot[1]=1;for(int col=2;col<=M.nu;col++){cpot[col]=cpot[col-1]+num[col-1];}for(int p=1;p<=M.tu;p++){int col=M.data[p].j;//提前得到在T.data中第q行int q=cpot[col];T.data[q].i=M.data[p].j;T.data[q].j=M.data[p].i;T.data[q].e=M.data[p].e;//这里之所以要加就是因为一行有多个元素++cpot[col];}}
}int main(){TSMatrix M,T;printf("请输入矩阵的行,列和非零元数: \n");scanf("%d %d %d",&M.mu,&M.nu,&M.tu);printf("请输入矩阵(三元组): \n");for(int i=1;i<=M.tu;i++){scanf("%d %d %d",&M.data[i].i,&M.data[i].j,&M.data[i].e);}printf("----------------------------------------------\n");TransposeSMatrix_1(M,T);printf("转置矩阵T: \n");for(int i=1;i<=T.tu;i++){printf("%d %d %d\n",T.data[i].i,T.data[i].j,T.data[i].e);}return 0;
}
/*
6 6 81 2 12
1 3 9
3 1 -3
3 6 14
4 3 24
5 2 18
6 1 15
6 4 -7
*/注:方法二比之前多用了两个辅助的数组空间num和cpot,但是从时间上来看的话,时间复杂度为O(nu+tu),如果tu的数量级和nu x mu同等,时间复杂度为O(nu x mu).
参考书籍《数据结构》(清华大学版)