流程
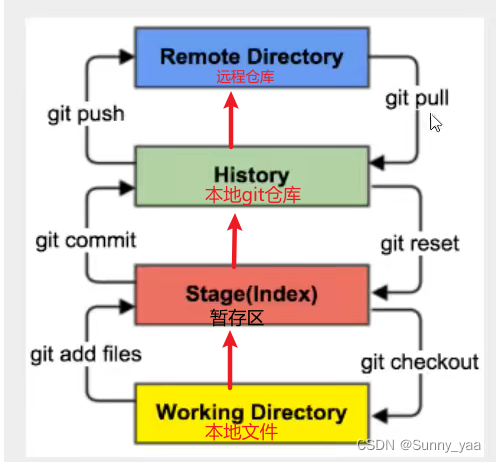
1在本地clone项目【保持与远程仓库一致】
此时已绑定远程仓库
git clone xxxx
2.添加文件
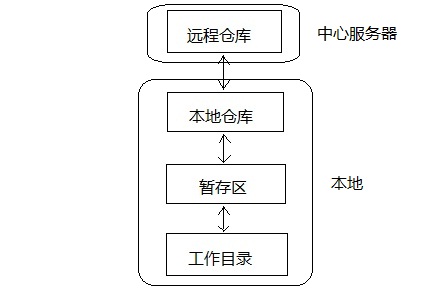
3.放到暂存区
git add .
4.提交到本地仓库
git commint -m "提示信息"
5推送到远程仓库
git push origin master
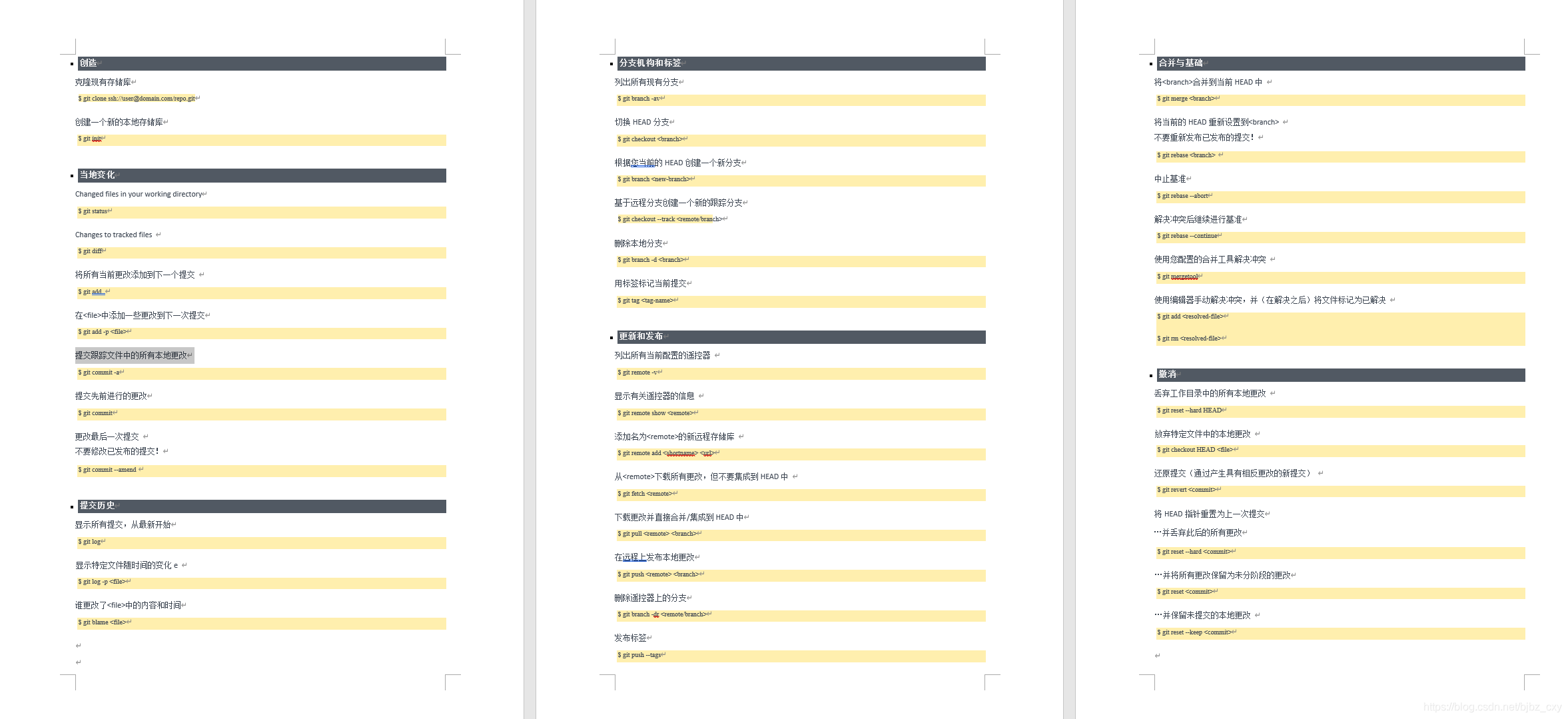
其他命令
分支命令
分支就是每个人开发 互不影响 之后再合并
1.创建分支
git branch
2.查看分支
git branch xxx 【xxx表示分支名】
- 切换分支
git checkout xxx 【xxx表示分支名】git checkout -b xxx 【xxx表示分支名,这里表示没有这个分支的话就创建分支并且切换到这个分支来】
仓库命令
绑定仓库
`git remote add xxx xxxxxxxxx 【第一个xxx代表给远程仓库起一个名字,第二个xxxx代表远程仓库的`地址】
查看仓库
git remote -v
1.自己创建一个空的git项目进行提交可能会出错:
这时因为本地仓库和远程仓库不一致缺少了东西 【主要原因是oschina中的README.md文件不在本地代码目录中】
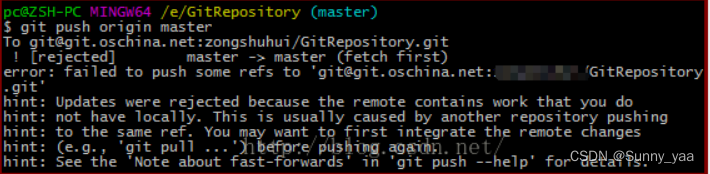
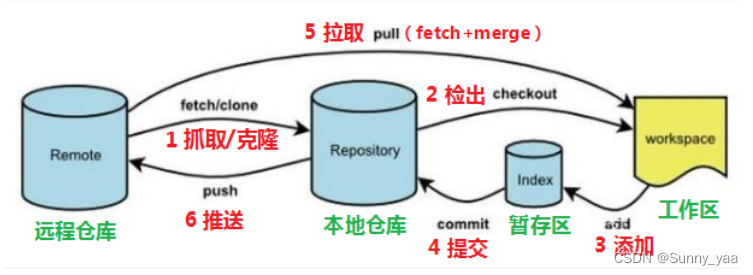
远程分支和本地的分支一样,我们可以进行merge操作,只是需要先把远端仓库里的更新都下载到本地,再进行操作。
抓取命令
git fetch [remote name] [branch name] // 抓取指令就是将仓库里的更新都抓取到本地,不会进行合并,如果不指定远端名称和分支名,则抓取所有分支。
拉取命令
git pull [remote name] [branch name] 拉取指令就是将远端仓库的修改拉到本地并自动进行合并,等同于fetch+merg如果不指定远端名称和分支名,则抓取所有并更新当前分支。
查看配置
所有的配置文件都保存在本地
git config -l
2.查看系统配置
git config --system --list
3.查看本地配置
git config --global --list
克隆命令
git clone 你复制的url
与远程仓库一致