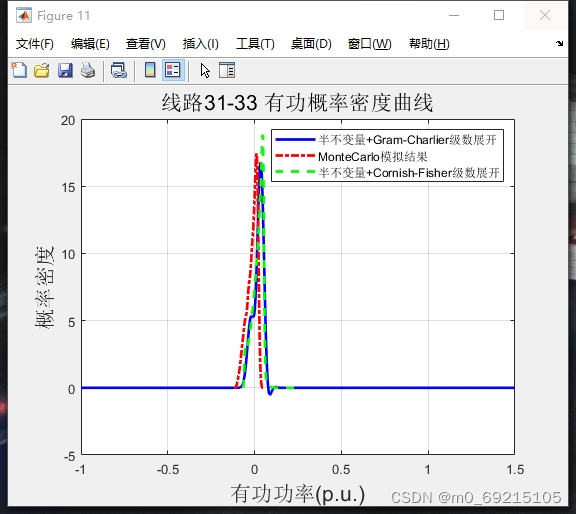
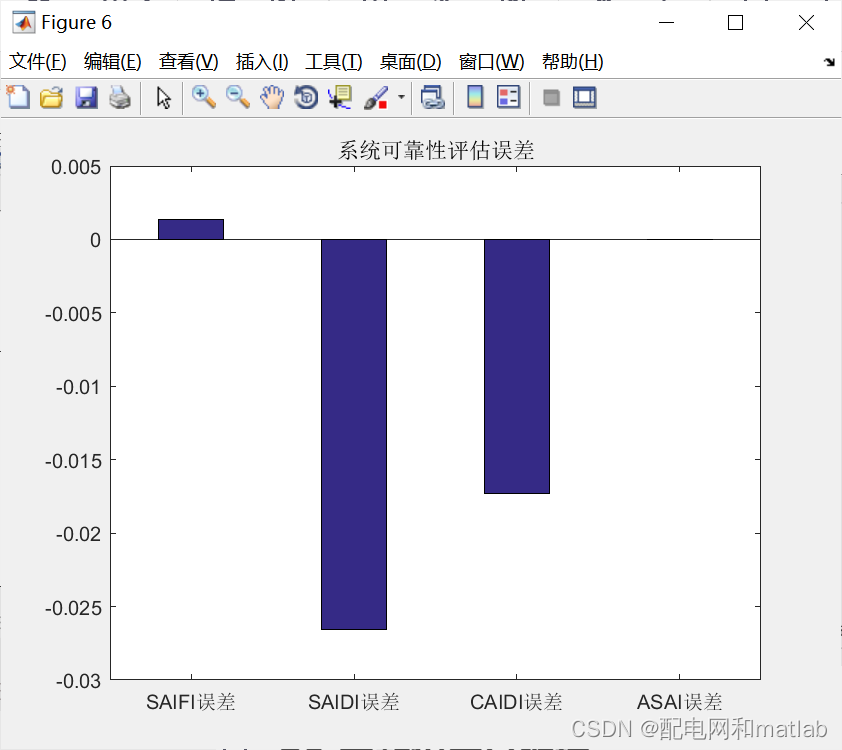
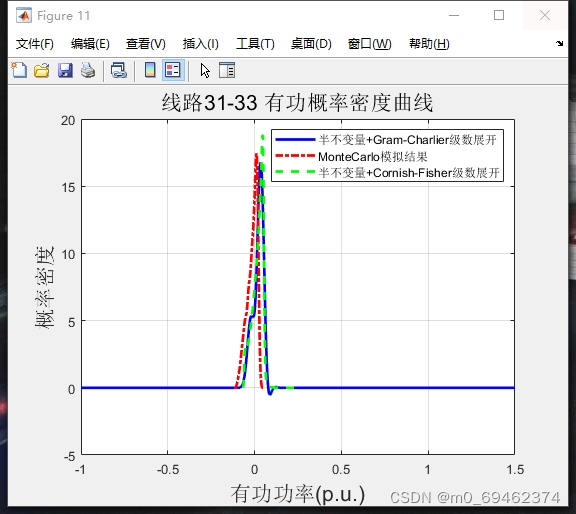
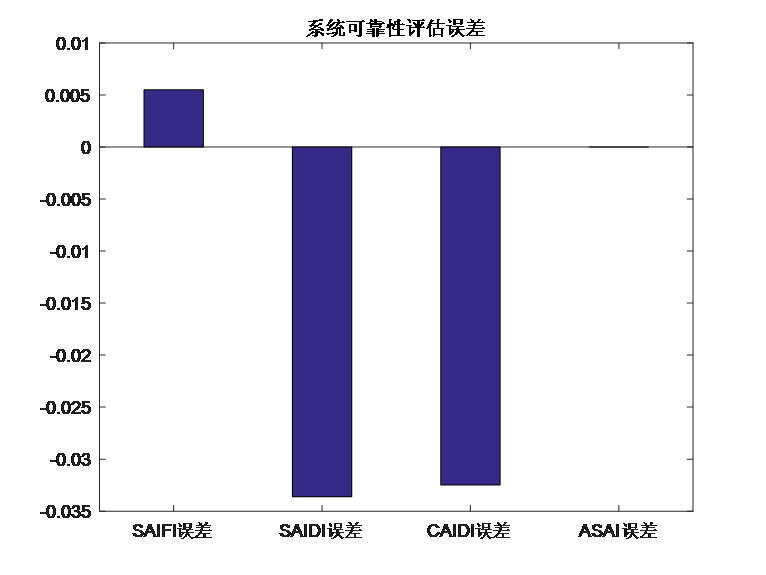
与需要空间、时间离散的有限差分法不同,随机法(例如蒙特卡洛方法)是另外一种模拟的方法,其无需进行空间和时间的离散。
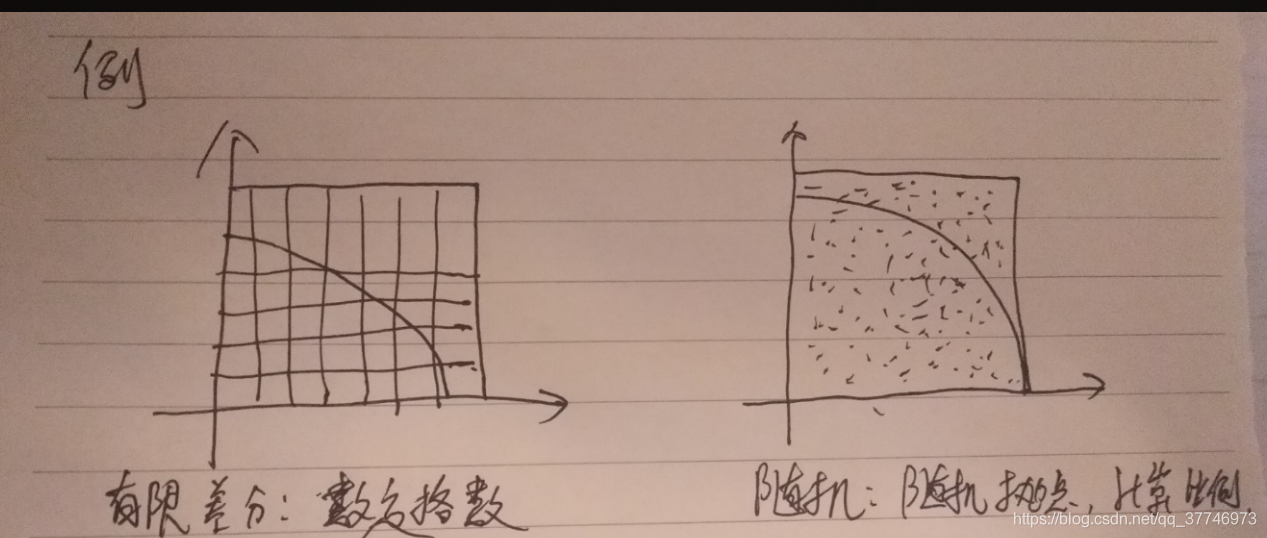
总结随机法的特点,基本思路,并以面积积分为例来分析两种方法的差异和各自的优缺点并恰出随机法适用的领域。
有限差分法
微分方程和积分微分方程数值解的方法。基本思想是把连续的定解区域用有限个离散点构成的 网格来代替, 这些离散点称作网格的节点;把连续定解区域上的连续变量的函数用在网格上定义的离散变量函数来近似;把原方程和定解条件中的微商用差商来近似, 积分用积分和来近似,于是原微分方程和定解条件就近似地代之以代数方程组,即有限差分方程组 , 解此方程组就可以得到原问题在离散点上的近似解。然后再利用插值方法便可以从离散解得到定解问题在整个区域上的近似解。
在采用 数值计算方法求解偏微分方程时,若将每一处导数由有限差分近似公式替代,从而把求解偏微分方程的问题转换成求解代数方程的问题,即所谓的有限差分法。有限差分法求解偏微分方程的步骤如下:
1、区域离散化,即把所给偏微分方程的求解区域细分成由有限个格点组成的网格;
2、近似替代,即采用有限差分公式替代每一个格点的导数;
3、逼近求解。换而言之,这一过程可以看作是用一个插值多项式及其微分来代替偏微分方程的解的过程
蒙特卡洛随机模拟法
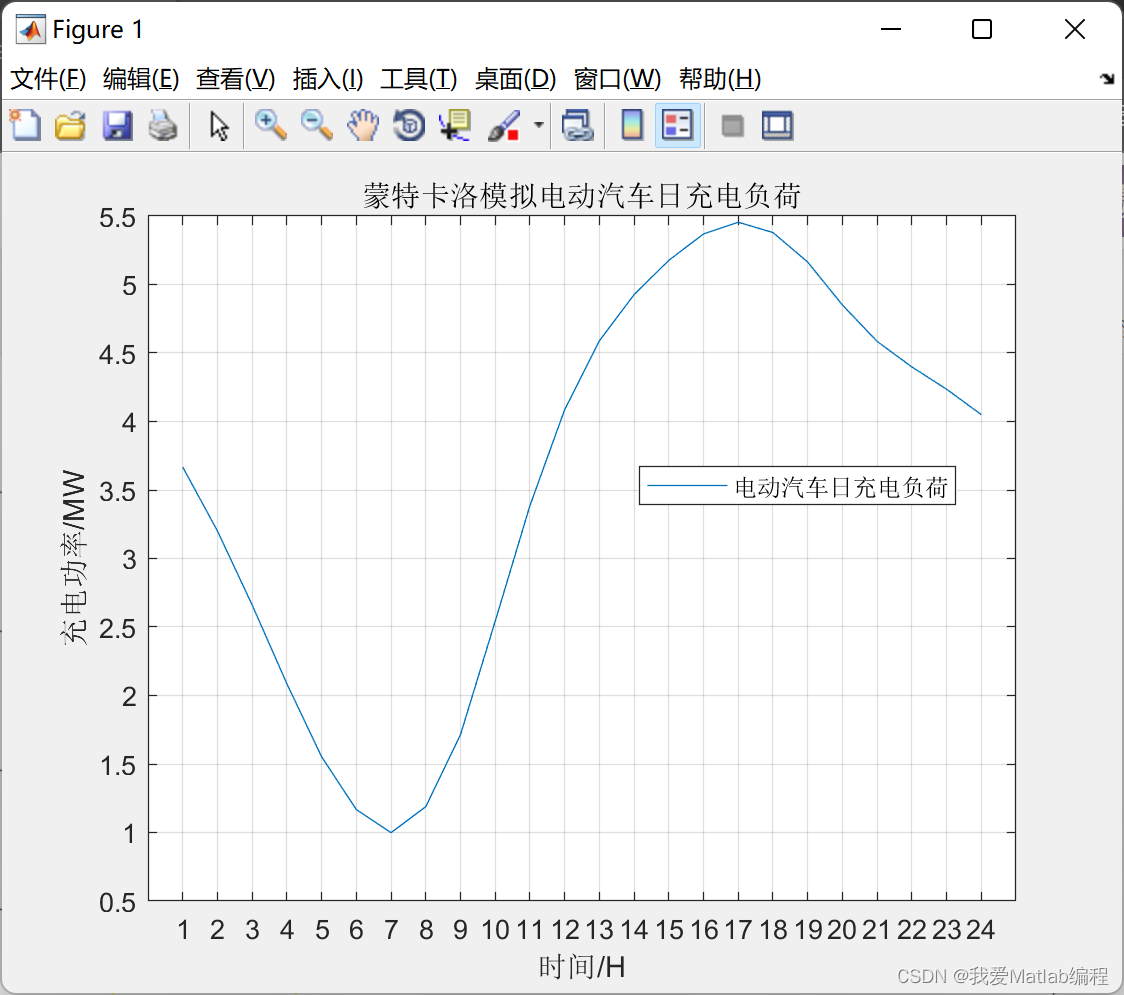
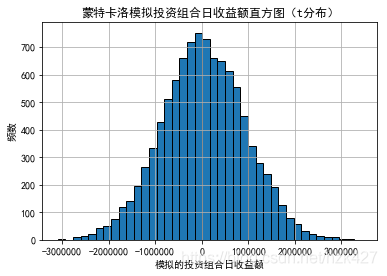
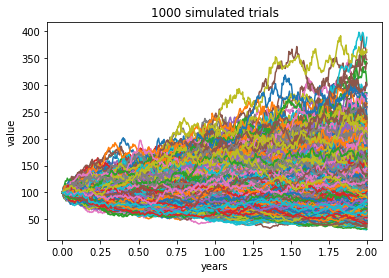
蒙特卡洛随机模拟法的原理是当问题或对象本身具有概率特征时,可以用计算机模拟的方法产生抽样结果,根据抽样计算统计量或者参数的值;随着模拟次数的增多,可以通过对各次统计量或参数的估计值求平均的方法得到稳定结论。
蒙特卡洛随机模拟法 - 实施步骤抽样计算统计量或者参数的值;随着模拟次数的增多,可以通过对各次统计量或参数的估计值求平均的方法得到稳定结论。
特点
基本思路
- 根据提出的问题构造一个简单、适用的概率模型或随机模型,使问题的解对应于该模型中随机变量的某些特征(如概率、均值和方差等),所构造的模型在主要特征参量方面要与实际问题或系统相一致。
- 根据模型中各个随机变量的分布,在计算机上产生随机数,实现一次模拟过程所需的足够数量的随机数。
- 根据概率模型的特点和随机变量的分布特性,设计和选取合适的抽样方法,并对每个随机变量进行抽样(包括直接抽样、分层抽样、相关抽样、重要抽样等)。
- 按照所建立的模型进行仿真试验、计算,求出问题的随机解。
- 统计分析模拟试验结果,给出问题的概率解以及解的精度估计。
抄了,然后刘涛老师看起来整整齐齐。。。。