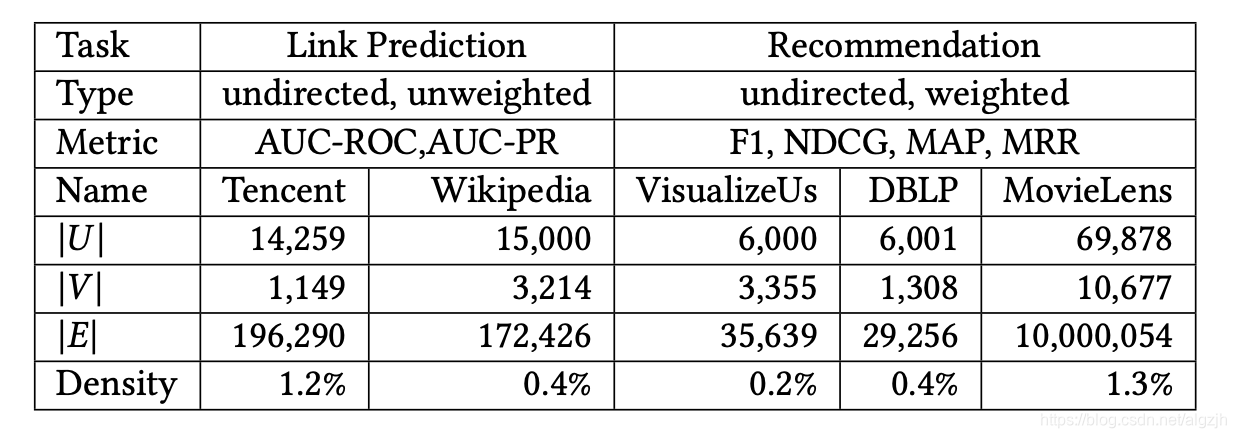
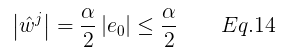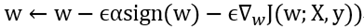Sparse Learning
本文的内容主要来自余凯老师在CVPR2012上给的Tutorial。前面在总结ScSPM和LLC的时候,引用了很多Tutorial上的图片。其实这个Tutorial感觉写的挺好的,所以这次把它大致用自己的语言描述一下。不过稀疏编码是前两年比较火的东西,现在火的是deep learning了。
1、What is sparse coding?
1988年,神经稀疏编码的概念由Mitchison提出,由牛津大学的Rolls等正式引用。灵长目动物颚叶视觉皮层和猫视觉皮层的电生理实验报告和一些相关模型的研究结果都说明了视觉皮层复杂刺激的表达是采用稀疏编码原则的。研究表明:初级视觉皮层V1区第四层有5000万个(相当于基函数),而负责视觉感知的视网膜和外侧膝状体的神经细胞只有100万个左右(理解为输出神经元)。说明稀疏编码是神经信息群体分布式表达的一种有效策略。1996年,加州大学伯克利分校的Olshausen等在Nature杂志发表论文指出:自然图像经过稀疏编码后得到的基函数类似V1区简单细胞感受野的反应特性(空间局部性、空间方向性、信息选择性)。
典型的sparse coding的过程分为训练和测试。
Training:给定一些训练样本(training samples)[ x1, x2, …, xm(in Rd)],学习一本字典的基(bases)[Φ1,Φ2……(also in Rd)]。可是用k-means等无监督的方法,也可以用优化的方法(这时training完了同时也得到了这些training samples的codes,这是一个LASSO和QP问题的循环迭代);
Coding:用优化的方法求解测试样本的codes(此时字典已经学得)。经典的方法是求解LASSO:
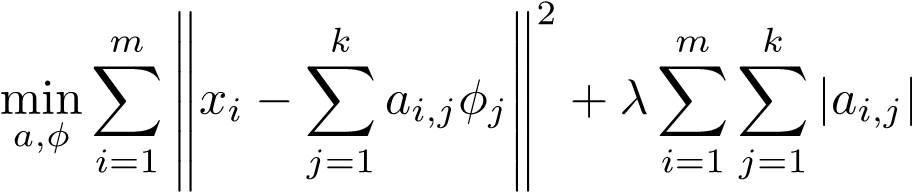
自我学习就是在Training的时候采用大量无标注的自然图像训练字典,然后对带标注的图像进行编码得到特征codes。
近十几年来,稀疏(sparsity)已经成为信号处理及其应用领域中处于第一位的概念之一。近来,研究人员又致力于过完备(overcomplete)信号表示的研究。这种表示不同于许多传统的表示。因为它能提供一个广阔范围的生成元素(atoms)。而冗余(redundant)信号表示的魅力正在于其能经济地(紧致)的表示一大类信号。对稀疏性的兴趣源自于新的抽样理论-压缩传感(compressed sensing)的发展,压缩传感是香农采样理论的一种替代,其利用信号本身是稀疏的这一先验,而香农理论是设计用于频率带宽有限的信号的。通过建立采样和稀疏的直接联系,压缩传感在大量的科学领域,如编码和信息论,信号和图像采集处理,医学成像,及地理和航天数据分析等都得到应用。压缩传感的另一贡献是许多传统的逆问题,如断层图像重建,可以看作压缩传感问题。这类病态(ill-posed)问题需要正则化。压缩传感对寻求系数性解的方法给出了强大的理论支持。
1、什么是稀疏性
设信号x是RN的有限维子空间向量,x=[x[1],x[2],…,x[N]], 如果x的绝大多数元素都为0,则x是严格稀疏的。
如果信号不稀疏,它却可能在某种变换域中稀疏。我们可以用T个基本波形(signal atoms)的线性组合来建模x,有
x= φa=sum(a[i]φ[i])
其中a[i]称为在字典φ中信号x的表示系数。
2、稀疏性的几个名词
1)原子(atom) 如前所述,原子是信号表示模板的元素。
2)字典(dictionary) 是许多原子的排序集合,可看作是一个NxT的矩阵,如果T>N, 则为过完备或冗余字典。
原子:字典的列向量。
完备字典与过完背字典:如果字典D中的原子恰能够张成n维的欧式空间,则字典D是完备的。如果m》n,字典D是冗余的,同时保证还能张成n维的欧式空间,则大字典D是过完备的。
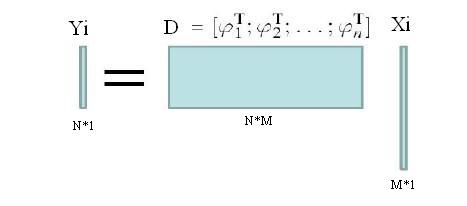
coding的过程就变成了已知Yi和D,求Xi的过程了。显然这是一个非齐次方程组求解的 问题,方程组有解的条件是rank(D)≤M,其中取等号时方程组有唯一解。过完备的定义是M>>N,所以此时 rank(D)≤N<<M,此时方程组有无穷多解。(你可能会问,这和最小化平方误差为目标函数不一样啊!其实求个导,就变成这个方程组 了。)这就是过完备造成的问题了。怎么办呢?办法就是对Xi做约束------稀疏的约束,这样Xi就有唯一解了。这就是需要加约束的原因。更多见:https://blog.csdn.net/zhangzhengyuan123123/article/details/38446185
2、Connections to RBMs, autoencoders
(1)式(经典的稀疏编码)有几个特点:
——系数a是稀疏的;
——a的维数一般比x的维数大;
——编码过程a=f(x)是一个非线性的关于x的隐函数(即我们没有f(x)的显示表达,因为求解LASSO没有解析解);
——重建过程x'=g(a)是一个线性的显示的关于a的函数(X’=ΣaiΦi)。
而RBM和自编码的特点则是:
——有显示的f(x);
——不会必然得到稀疏的a,但是如果我们增加稀疏的约束(如稀疏自编码,稀疏RBM),通常能得到更好的效果(进一步说明sparse helps learning)。
从广义上说,满足这么几个条件的编码方式a=f(x)都可以叫稀疏编码:
1) a是稀疏的,且通常具有比x更高的维数;
2) f(x)是一个非线性的映射;(jiang1st2010注:该条要求存疑,见下面解释。)
3) 重建的过程x'=g(a),使得重建后的x'与x相似。
因此,sparse RBM,sparse auto-encoder,甚至VQ都可以算是一种sparse coding。(jiang1st2010注:第二条要求称f(x)是一个非线性映射,然而SPM中用到的VQ是一个线性映射,原因可以参见这里和这里。余凯老师也是LLC论文的作者,似乎存在矛盾?不过这是个小问题了,没必要深究。)
3、Sparse activations vs. sparse models
现在可以用a=f(x)表示稀疏编码的问题了。它可以分解成两种情况:
1)sparse model:f(x)的参数是稀疏的
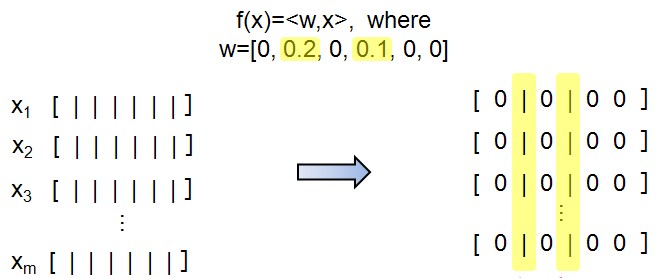
--例如:LASSO f(x)=<w,x>,其中w要求是稀疏的。(jiang1st2010注:这个例子中f(x)也是线性的!)
--这是一个特征选择的问题:所有的x都挑选相同的特征子集。
--hot topic.
2)sparse activation:f(x)的输出是稀疏的
--就是说a是稀疏的。
--这是特征学习的问题:不同的x会激活不懂的特征子集。
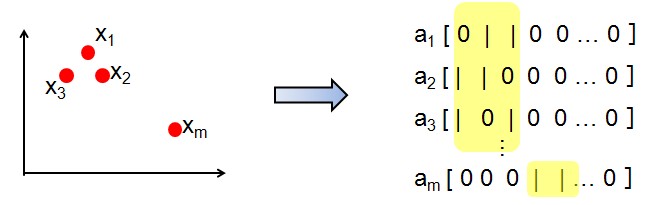
4、Sparsity vs. locality
其实这个问题在这里已经谈过了。简单的说就是sparsity不一定导致locality,而locality肯定是sparse的。sparse不比locality好,因为locality具有smooth的特性(即相邻的x编码后的f(x)也是相邻的),而仅仅sparse不能保证smooth。smooth的特性对classification会具有更好的效果,并且设计f(x)时,应尽量保证相似的x在它们的codes中有相似的非0的维度。
Tutorial上展示了(1)中取不同的λ,字典中各项呈现的效果:
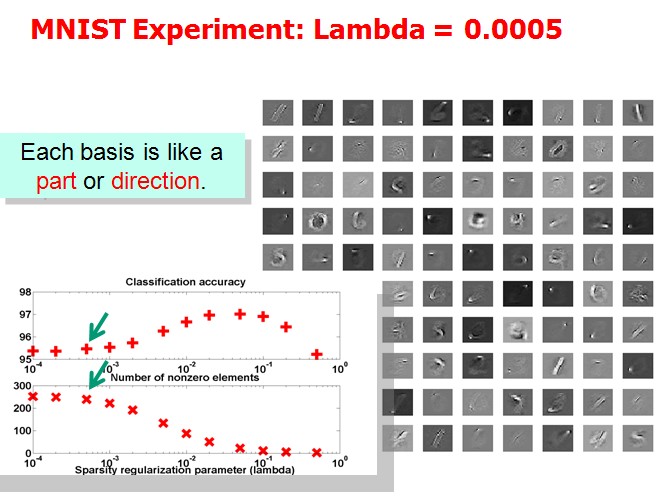
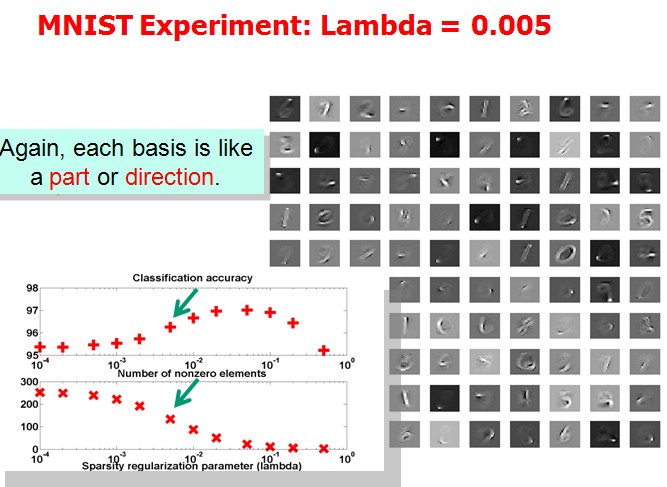
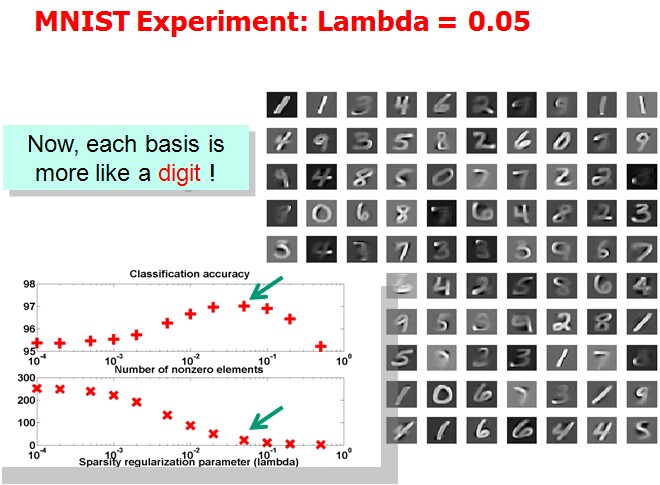
作者想说明的问题是分类效果越好的情况下,basis会更清晰地表现出属于某几个特定的类。但是我没太看明白。
5、Hierarchical sparse coding
这里图3曾说明了SIFT本身就是一个Coding+Pooling的过程,所以SPM是一个两层的Coding+Pooling。而Hierarchical sparse coding就是两层的coding都是sparse coding,如下图:
整个HSC的第一层就从pixel层级开始(不需要手动设计SIFT特征了),经过两层SC后,形成codes。这个过程可以从无标注的数据中学习,就是self-taught learning。从pixel层级开始,这点和DNN啥的很像了。
从结果来看,HSC的性能会比SIFT+SC稍微好些。
Tutorial的最后列举了关于SC的其他主题,我也不懂,这里就不废话了。
【转载】:http://blog.csdn.net/jwh_bupt/article/details/9902949