前些天发现一个通俗易懂，风趣幽默的人工智能学习网站：

传送门

A 简介

1 历史
最初的元胞自动机是由冯 · 诺依曼在 1950 年代为模拟生物细胞的自我复制而提出的. 但是并未受到学术界重视.
1970 年, 剑桥大学的约翰 · 何顿 · 康威设计了一个电脑游戏 “生命游戏” 后, 元胞自动机才吸引了科学家们的注意.

1983 年 S.Wolfram 发表了一系列论文. 对初等元胞机 256 种规则所产生的模型进行了深入研究, 并用熵来描述其演化行为, 将细胞自动机分为平稳型, 周期型, 混沌型和复杂型.

2 应用

社会学: 元胞自动机经常用于研究个人行为的社会性, 流行现象. 例如人口迁移, 公共场所内人员的疏散, 流行病传播.
图形学: 元胞自动机以其特有的结构的简单性, 内在的并行性以及复杂计算的能力成为密码学中研究的热点方向之一
物理学: 在物理学中, 元胞自动机已成功的应用于流体, 磁场, 电场, 热传导等的模拟. 例如格子气自动机.

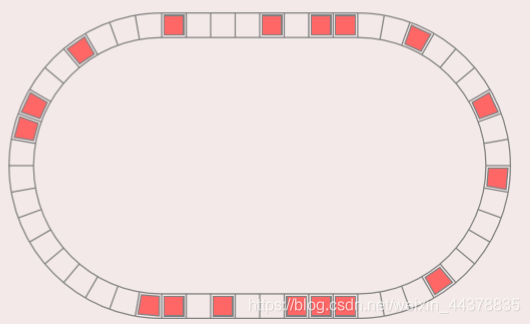
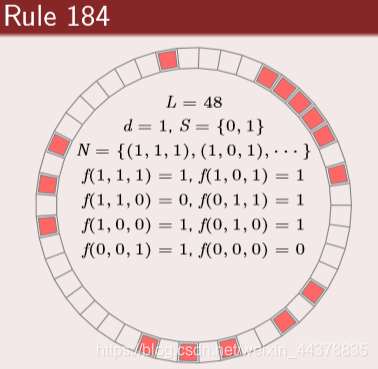
3 一维元胞自动机——交通规则
定义：

元胞分布于一维线性网格上.
元胞仅具有车和空两种状态.
元胞状态由周围两邻居决定.

规则：研究的变化对象只是中间的格子，后面的车子要比前面的车子起步延迟1格。
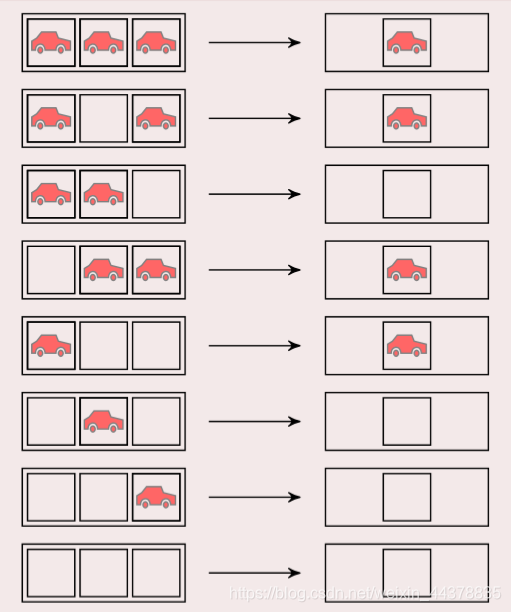
在这里插入图片描述

4 二维元胞自动机——生命游戏
定义：

元胞分布于二维方型网格上.
元胞仅具有生和死两种状态.
元胞状态由周围八邻居决定.

规则：
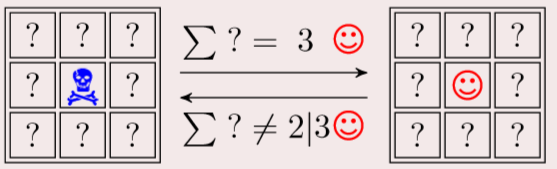
在这里插入图片描述

骷髅：死亡；笑脸：生存
周围有三个笑脸，则中间变为笑脸
少于两个笑脸或者多于三个，中间则变死亡。

5 什么是元胞自动机
离散的系统: 元胞是定义在有限的时间和空间上的, 并且元胞的状态是有限.
动力学系统: 元胞自动机的举止行为具有动力学特征.
简单与复杂: 元胞自动机用简单规则控制相互作用的元胞模拟复杂世界.
在这里插入图片描述

6 构成要素

（1）元胞 (Cell)
在这里插入图片描述
元胞是元胞自动机基本单元：

状态: 每一个元胞都有记忆贮存状态的功能.
离散: 简单情况下, 元胞只有两种可能状态; 较复杂情况下, 元胞具有多种状态.
更新: 元胞的状态都安照动力规则不断更新.

（2）网格 (Lattice)
不同维网格
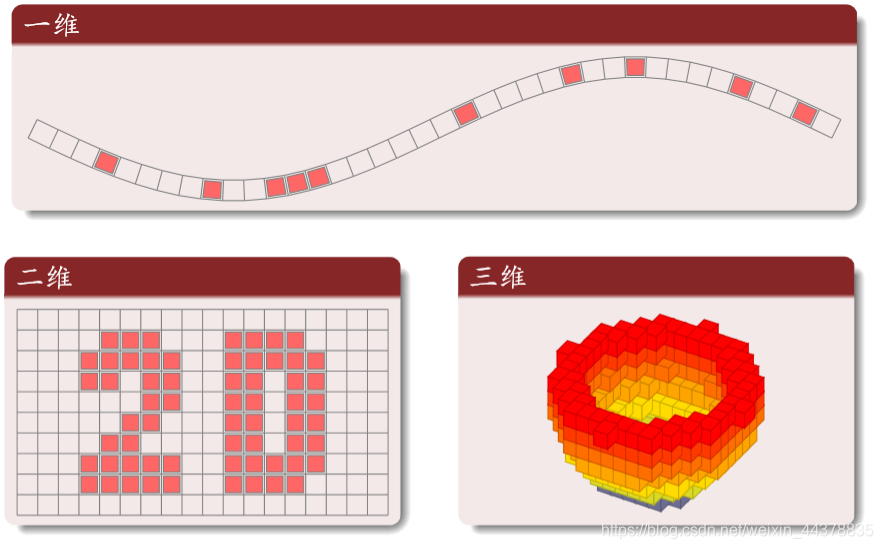
在这里插入图片描述

常用二维网格
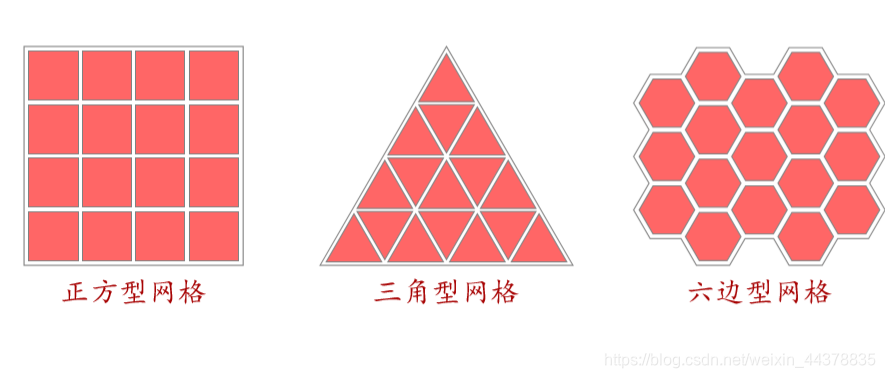
在这里插入图片描述

（3）邻居 (Neighborhood)
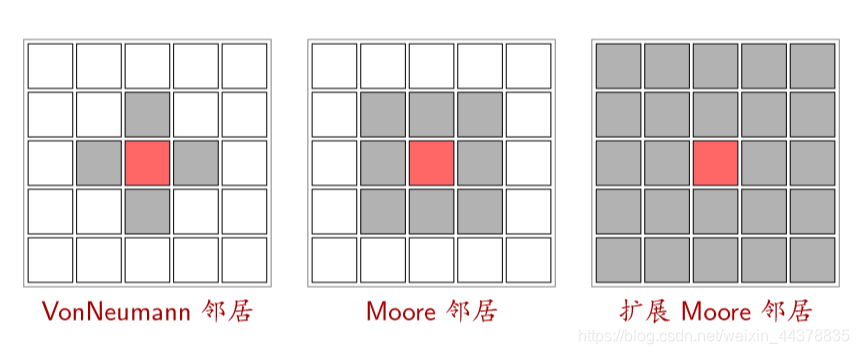
在这里插入图片描述

（4）边界 (Boundary)
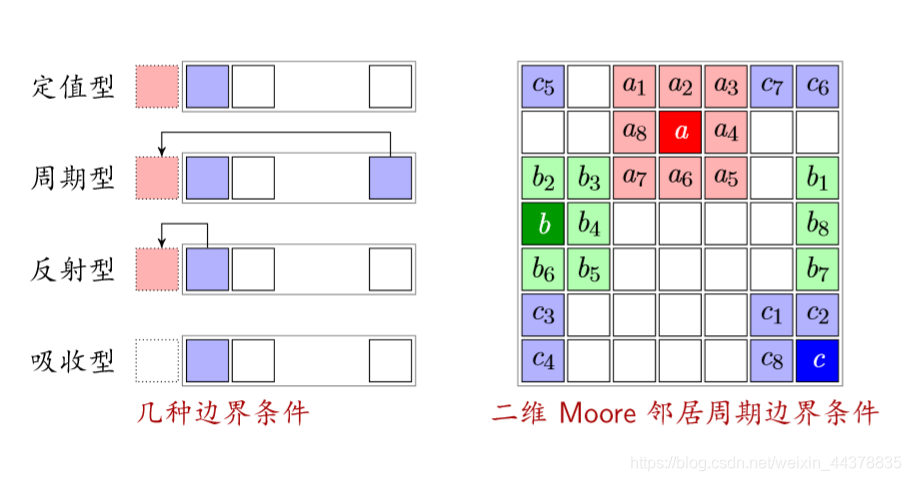
在这里插入图片描述
反射型：以自己作为边界的状态
吸收型：不管边界（车开到边界就消失）

（5）规则（状态转移函数）
定义：根据元胞当前状态及其邻居状况确定下一时刻该元胞状态的动力学函数, 简单讲, 就是一个状态转移函数.

分类：

总和型: 某元胞下时刻的状态取决于且仅取决于它所有邻居的当前状态以及自身的当前状态.
合法型: 总和型规则属于合法型规则. 但如果把元胞自动机的规则限制为总和型, 会使元胞自动机具有局限性.

（6）森林火灾
在这里插入图片描述

绿色：树木；红色：火；黑色：空地。
三种状态循环转化：
树：周围有火或者被闪电击中就变成火。
空地：以概率p变为树木

理性分析：红为火；灰为空地；绿是树
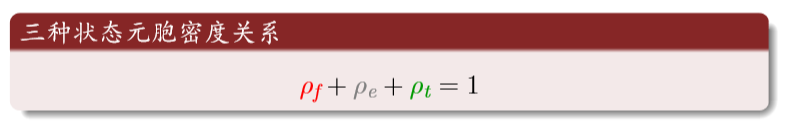
在这里插入图片描述
元胞三种状态的密度和为1

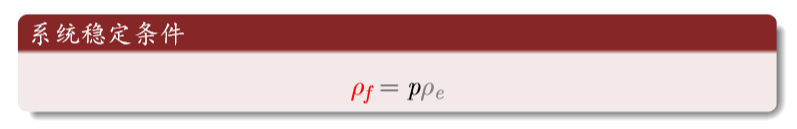
火转化为空地的密度等于空地转换为树的密度（新长出来的树等于烧没的树）

$f$ 是闪电的概率:远远小于树生成的概率； $T_{smax}$ 是一大群树被火烧的时间尺度

程序实现
周期性边界条件
购进啊
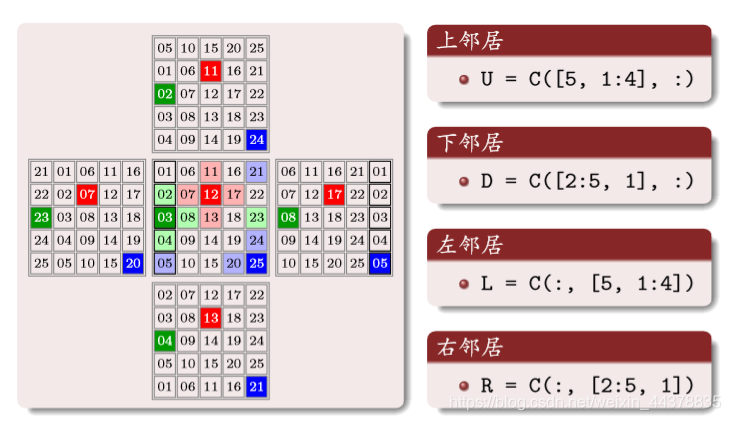
在这里插入图片描述
其中的数字为编号
构建邻居矩阵

上面矩阵中的数字编号，对应原矩阵相同位置编号的上邻居编号，一一对应
同样道理：
在这里插入图片描述

% simulate forest fire with cellular automata
% zhou lvwen: zhou.lv.wen@gmail.com
% August 15 2010 
n = 300;                           % 定义表示森林的矩阵大小
Plight = 5e-6; Pgrowth = 1e-2;     % 定义闪电和生长的概率  
UL = [n 1:n-1]; DR = [2:n 1];      % 定义上左，下右邻居
veg=zeros(n,n);                    % 初始化表示森林的矩阵
imh = image(cat(3,veg,veg,veg));   % 可视化表示森林的矩阵
% veg = 空地为0 着火为1 树木为2
for i=1:3000 sum =            (veg(UL,:)==1) + ...(veg(:,UL)==1)     +      (veg(:,DR)==1) + ...(veg(DR,:)==1);  % 计算出所有格子有几个邻居是着火的
% 根据规则更新森林矩阵：是否树=是否树-是否着火的树+是否新生的树（0-1运算）veg = 2*(veg==2) - ...( (veg==2) & (sum>0 | (rand(n,n)<Plight)) ) + ...     2*((veg==0) & rand(n,n)<Pgrowth) ;  set(imh, 'cdata', cat(3,(veg==1),(veg==2),zeros(n)) )drawnow                         % 可视化表示森林的矩阵
end

（7）交通概念
车距和密度
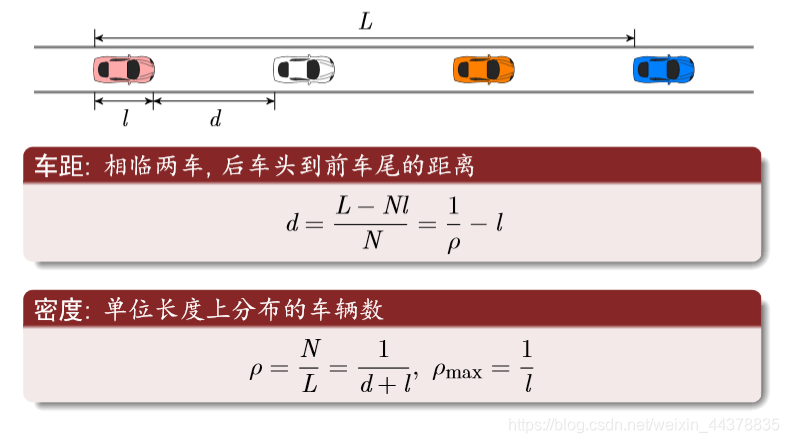
在这里插入图片描述

流量方程
在这里插入图片描述

守恒方程
在这里插入图片描述

时空轨迹（横轴是空间纵轴为时间）

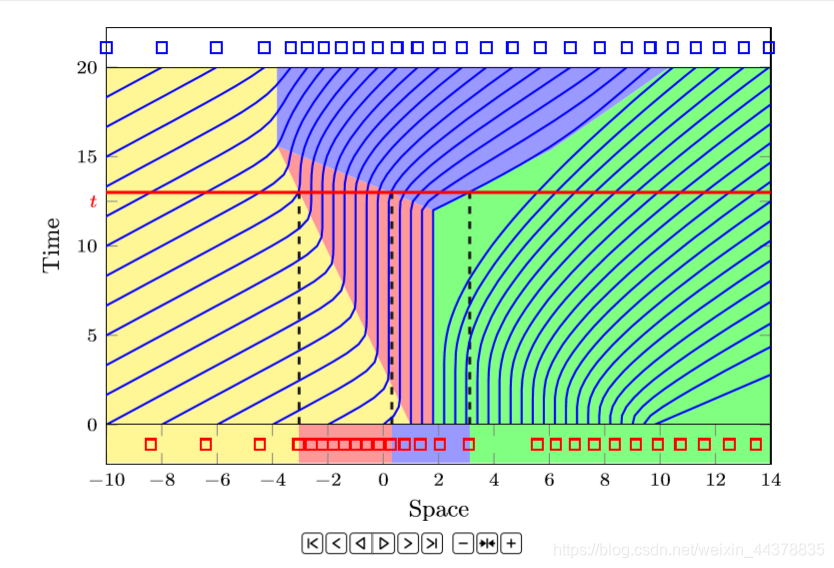
在这里插入图片描述

红线横线与蓝色交点表示每个时间车的位置。
如果是竖线则表示车子在该位置对应的时间

宏观连续模型：
在这里插入图片描述
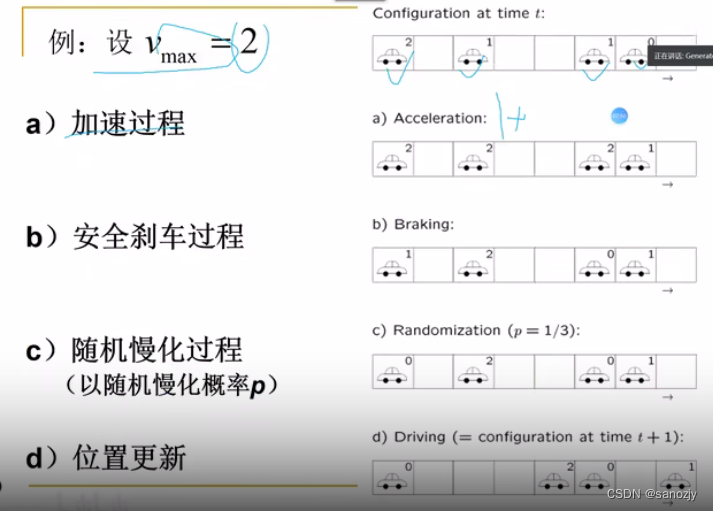
最常用的规则：

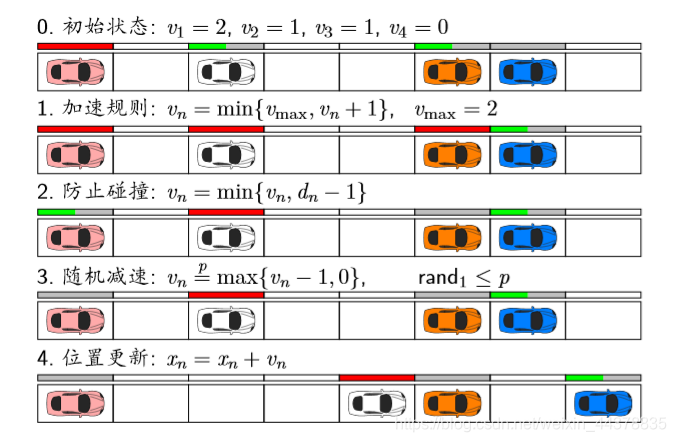
红色条表示速度是满的。

1 加速规则：不能超过 $v_{max}（2格/s）$
2 防止碰撞：不能超过车距

理论分析：
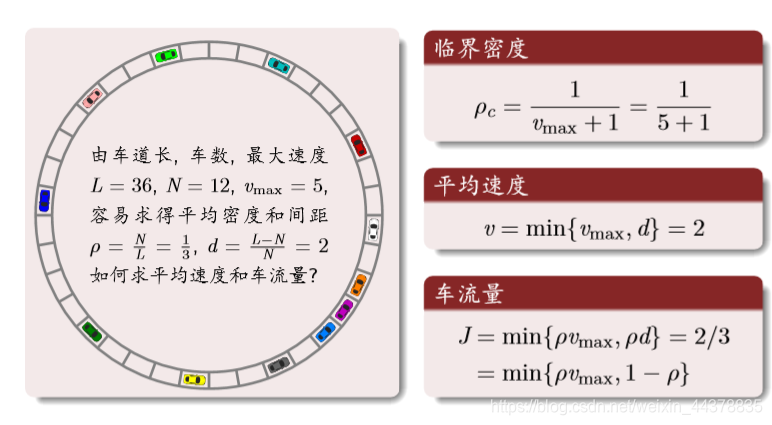
在这里插入图片描述

结果分析: 密度与流量
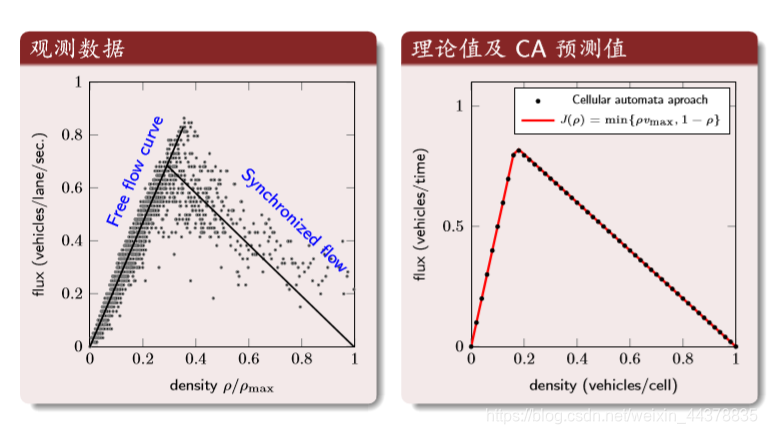
在这里插入图片描述
第一个图：横坐标是归一化后的密度，纵坐标是车流量。第二个图：理论值与CA的结果

结果分析: 时空轨迹
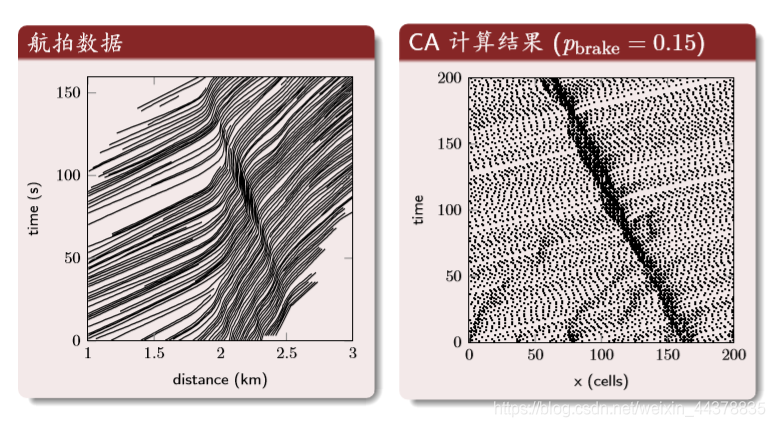
在这里插入图片描述
中间的深色区域是交通堵塞的区域。
ns.m

function [rho, flux, vmean] = ns(rho, p, L, tmax, animation, spacetime)
vmax = 5;                           %最大速度
% place a distribution with density
ncar = round(L*rho);                % 车数量=L*rho
rho = ncar/L;
x = sort(randsample(1:L, ncar));    % 从1到L中随机采ncar格样并排序
v = vmax * ones(1,ncar);            % 初始化所有车子su'du1为vmax
flux = 0;                  % number of cars that pass through the end
vmean = 0;
road = zeros(tmax, L);
for t = 1:tmax% 加速规则v = min(v+1, vmax);%防止碰撞gaps = gaplength(x,L); % 获得每一辆车到前面一辆车的距离v = min(v, gaps-1);% 随机减速vdrops = ( rand(1,ncar)<p );v = max(v-vdrops,0);% 更新位置x = x + v;passed = x>L;          % 车走过整个路段x(passed) = x(passed) - L;% 回到起点if t>tmax/2flux = flux + sum(v/L); %平均流量vmean = vmean + mean(v);endroad(t,x) = 1;
end
flux = flux/(tmax/2);
vmean = vmean/(tmax/2);
if spacetime; figure;imagesc(road);colormap([1,1,1;0,0,0]);axis image; end% -------------------------------------------------------------------------
function gaps = gaplength(x,L)
% 计算车距
ncar = length(x);
gaps=zeros(1, ncar);
if ncar>0gaps = x([2:end 1]) -x;   % d(i)=x(i+1)-x(i)gaps(gaps<=0) = gaps(gaps<=0)+L; %d(i)=d(i)+L,if d(i)<0
end
nsity = 0:0.02:1;
roadlength = 100;
vmax = 5;
tmax = 200;
pbrak = 0;
flux = [];
vmean = [];
for rho = density[R, J, V] = ns(rho, pbrak, roadlength, tmax, 0, 0);flux = [flux; J];vmean = [vmean; V];
end
% ------------------------- density vs. volecity --------------------------
figure
plot(density, vmean,'k.','markersize',15);
hold on
plot(density,min(vmax, 1./density-1),'-r','linewidth',2)
ylim([0,5.55])
legend({'Cellular automata aproach', ...'$v(\rho) = \min\{v_{\max}, 1/\rho-1\}$'}, ...'interpreter','latex')
xlabel('density in vehicles/cell')
ylabel('velocity in cell/time')
% --------------------------- density vs. flux ----------------------------
figure
plot(density, flux,'k.','markersize',15);
hold on;
plot(density,min(density*vmax, 1-density),'-r','linewidth',2)
legend({'Cellular automata aproach', ...'$J(\rho) = \min\{\rho\cdot v_{\max}, 1-\rho\}$'}, ...'interpreter','latex')
xlabel('density in vehicles/cell')
ylabel('flux in vehicles/time')

density = 0:0.02:1;
roadlength = 100;
vmax = 5;
tmax = 200;
pbrak = 0;
flux = [];
vmean = [];
for rho = density[R, J, V] = ns(rho, pbrak, roadlength, tmax, 0, 0);flux = [flux; J];vmean = [vmean; V];
end
% ------------------------- density vs. volecity --------------------------
figure
plot(density, vmean,'k.','markersize',15);
hold on
plot(density,min(vmax, 1./density-1),'-r','linewidth',2)
ylim([0,5.55])
legend({'Cellular automata aproach', ...'$v(\rho) = \min\{v_{\max}, 1/\rho-1\}$'}, ...'interpreter','latex')
xlabel('density in vehicles/cell')
ylabel('velocity in cell/time')
% --------------------------- density vs. flux ----------------------------
figure
plot(density, flux,'k.','markersize',15);
hold on;
plot(density,min(density*vmax, 1-density),'-r','linewidth',2)
legend({'Cellular automata aproach', ...'$J(\rho) = \min\{\rho\cdot v_{\max}, 1-\rho\}$'}, ...'interpreter','latex')
xlabel('density in vehicles/cell')
ylabel('flux in vehicles/time')