第三十四篇 特征多项式法求对称三对角矩阵的特征值

特征多项式

在之前的篇章中介绍过的，一个矩阵的特征值可以形成一个n阶多项式的根，称为“特征多项式”。线性方程的求解方法可以用来求这些根，详情可以翻看我之前写过的文章。但这并不是一个有效方法。还有一些更有效的方法是基于特征多项式的性质，当要求解特征值的矩阵是一个三对角矩阵时，使用这种性质可以很容易求出特征值。因此这种方法与前面描述的Householder法转换成三对角矩阵或Lanczos法转换成三对角矩阵变换结合使用非常方便。

计算三对角矩阵的行列式值

在上一篇中，已经介绍过将矩阵转化为三对角等价的非迭代方法。得到n × n系统的特征值方程为

因此，这个问题就成了求行列式方程的根的问题

虽然我们不能直接找到这些根，但想一下上面方程左边行列式的计算
对于 n = 1

对于 n = 2

对于n = 3

可以看出一个递归关系，使det3(λ)可以简单地从det2(λ)和det1(λ)的值来评估。如果使det0(λ) = 1，一般的递归式可以写成下面这样。

因此，对于任何λ值，都可以很快计算λ，并且如果知道根λ = 0的范围，它的值可以通过二分法来计算。难点是把λ代入方程确保它是一个根。由于第二个方程的“主次方程”所具有的一个特殊性质，即“Sturm序列”性质，使得这个问题变得容易得多。

Sturm序列性质

对于n = 5，第二个方程左边的例子如下:

|a |的主余子式是虚线勾勒出的子矩阵的行列式，即消去[A]的第n行、(n−1)行得到。[A]的λ值和它的余子式的λ值在下面给出。

从上面的推导中得到，它们的根，也就是它们的特征值。从上表可以看出，[A]n， [A]n−1，[A]n−2等的每一个后续的特征值集合总是从前一个集合插值出来的，即[Ai−1]的特征值总是出现在[Ai]的特征值之间的间隙中。对于所有对称[A]，这种分离性质被发现，称为“Sturm序列”性质。
它最有用的结论是，对于任何猜测的λ， i = 0,1,2，···，n时，deti(λ)符号变化的次数等于比λ值小[A]的的特征值数量。当计数符号变化时，应该设置det0(λ) = 1，并规定deti(λ) = 0不算作变化。
对于上面所示的具体例子，假设λ = 4，计算deti(4)， i = 0,1,2，···，5，得出表格

从det0(4) = 1.0开始，沿表向下移动，我们看到5个符号变化，因此有5个特征值小于4。
现在让我们试试λ = 3.5。在本例中，表格是


我们只看到4个符号变化，因此有4个小于3。5的特征值。这两个结果表明，最大特征值在3.5 <λ< 4范围内。下表总结了λ值的选择结果。

程序如下：
本程序使用之前的文章中得出的三对角矩阵，其中有一个主程序和检查收敛的子程序check

#LR转化求特征值
import numpy as np
import B
n=5;j=1;al=2.5;almax=5.0;tol=1e-5;limit=100
det=np.zeros(n+1)
alpha=np.array([2.0,2.0,2.0,2.0,2.0])
beta=np.array([-1.0,-1.0,-1.0,-1.0])
print('主对角线项',alpha)
print('非主对角线项',beta)
print('需要的特征值，1=最大,2=第二大...',j)
print('特征值   行列式的值    少于此值的根的数量')
iters=0;det[n]=1.0;aold=almax
while(True):iters=iters+1det[0]=alpha[0]-alfor i in range(2,n+1):det[i-1]=(alpha[i-1]-al)*det[i-2]-beta[i-2]*beta[i-2]*det[i-3]number=0for i in range(1,n+1):if abs(det[i-1])<1.0e-20:continueif abs(det[i-2])<1.0e-20:sign=det[i-1]*det[i-3]else:sign=det[i-1]*det[i-2]if sign<1.0e-20:number=number+1if number<=n-j:oldl=al;al=0.5*(al+almax)else:almax=al;al=0.5*(oldl+al)if det[n-1]<1.0e-20:number=number-1if j%2==0:number=number-1print('{:13.4e}'.format(al),end='')print('{:13.4e}'.format(det[n-1]),end='    ')print(number)if B.check(al,aold,tol) or iters==limit:breakaold=al
print('迭代到收敛次数',iters)

check

def check(x1,x0,tol):check=not abs(x1-x0)/abs(x0)>tolreturn check

终端输出结果如下

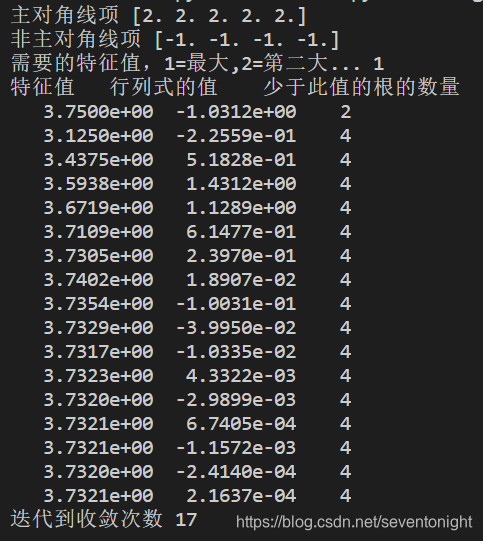
可知，得到的最大特征值为3.7321。