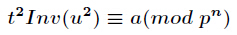昨天训练的时候遇到一道题怎么也不会做,在网上搜了题解之后第一次听说了二次剩余,看了一天各种dalao的博客,在这里总结一下自己所理解的二次剩余及其用法。
1,什么是二次剩余?
2,二次剩余有什么用?
※说白了就是如果该二次同余方程有解,那么n可以在模p的意义下开根号。
3,二次同余方程如何求解?
这一部分内容参考了这两篇文章:
http://blog.csdn.net/a_crazy_czy/article/details/51959546
http://blog.csdn.net/acdreamers/article/details/10182281
首先,以下解法有一个前提,就是p必须要是奇素数。
接下来我们引入一个新概念:勒让德符号(legender symbol)
它的定义如下
由此再引出一个定理
接下来是最后一个定理
有了最后一个定理,我们就可以通过随机选择a的值来找到一个满足条件的解。之前的链接里有详细地解释为何可以随机取a的值,总的来说就是找到正解所需的次数的期望只有2。所以随机取a的值可以很快地找到一个解,代码如下。
#include <iostream>
#include <ctime>
using namespace std;
typedef long long LL;
#define random(a,b) (rand()%(b-a+1)+a)
LL quick_mod(LL a, LL b, LL c) { LL ans = 1; while (b) { if (b % 2 == 1)ans = (ans*a) % c; b /= 2; a = (a*a) % c; }return ans; }LL p;
LL w;//二次域的D值
bool ok;//是否有解struct QuadraticField//二次域
{LL x, y;QuadraticField operator*(QuadraticField T)//二次域乘法重载{QuadraticField ans;ans.x = (this->x*T.x%p + this->y*T.y%p*w%p) % p;ans.y = (this->x*T.y%p + this->y*T.x%p) % p;return ans;}QuadraticField operator^(LL b)//二次域快速幂{QuadraticField ans;QuadraticField a = *this;ans.x = 1;ans.y = 0;while (b){if (b & 1){ans = ans*a;b--;}b /= 2;a = a*a;}return ans;}
};LL Legender(LL a)//求勒让德符号
{LL ans=quick_mod(a, (p - 1) / 2, p);if (ans + 1 == p)//如果ans的值为-1,%p之后会变成p-1。return -1;elsereturn ans;
}LL Getw(LL n, LL a)//根据随机出来a的值确定对应w的值
{return ((a*a - n) % p + p) % p;//防爆处理
}LL Solve(LL n)
{LL a;if (p == 2)//当p为2的时候,n只会是0或1,然后0和1就是对应的解return n;if (Legender(n) == -1)//无解ok = false;srand((unsigned)time(NULL));while (1)//随机a的值直到有解{a = random(0, p - 1);w = Getw(n, a);if (Legender(w) == -1)break;}QuadraticField ans,res;res.x = a;res.y = 1;//res的值就是a+根号wans = res ^ ((p + 1) / 2);return ans.x;
}int main()
{LL n,ans1,ans2;while (scanf("%lld%lld",&n,&p)!=EOF){ok = true;n %= p;ans1 = Solve(n);ans2 = p - ans1;//一组解的和是pif (!ok){printf("No root\n");continue;}if (ans1 == ans2)printf("%lld\n", ans1);elseprintf("%lld %lld\n", ans1, ans2);}
}