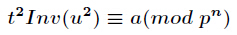• 近日备考学习二次剩余理论，其中了解到勒让德符号这个相比欧拉定理更加方便判断一个正整数在一个模数下是否为二次剩余；

• 基于勒让德符号理论的学习，本文旨在通过程序来实现基于勒让德符号的二次剩余判断方法；

• 本文着重点在于运算过程的展示及功能代码的实现，具体的理论细节还请读者独立了解；

• 本文使用C语言来实现功能，而且相较于其他简单实现的方式更倾向于了解其中的定理运算过程，难免较为繁琐，如有不足之处大可指出；

目录

手工运算

代码实现

测试结果(读者可手工运算验证)

---

手工运算

---

 

代码实现

---

#include <stdio.h>
#include <math.h>
#include <stdlib.h>typedef unsigned uint;// 判断互素
int gcd(uint a, uint b) {if (b == 0) {return a;}return gcd(b, a % b);
}// 判断素性
int is_prime(uint n) {uint rt = (uint)sqrt(n);for (int i = 2; i < rt; i++) {if (n % i == 0) return 0;}return 1;
}// 欧拉定理(未调用)
int Euler_T(uint a, uint p) {if (gcd(a, p) != 1)return 0;uint ex = (p - 1) / 2;uint eu = (uint)pow(a, ex) % p;if (eu % p == 1) {return 1;} else if (eu % p == p - 1) {return -1;} else {return 0;}
}// 勒让德符号运算
int Legendre(uint a, uint n) {uint p = a, q = n;int f = 1; // 正负表示while (p != 1 && q != 1) {if ((p & 1 == 1) && (q & 1 == 1)) {if ((p % 4 != 1) && (q % 4 != 1)) {f *= -1;}uint t = q;q = p;p = t;p %= q;}while (gcd(p, 2) > 1) {p /= 2;}}if (f == 1) {return 1;} else {return 0;}
}// 主程序测试
int main() {int a, n; scanf("%u%u", &a, &n);if (Legendre(a, n)) {printf("Quadratic Residue!\n");} else {printf("Not Quadratic Residue..\n");}return 0;
}

测试结果(读者可手工运算验证)

---