就是用来求解 x 2 ≡ n   m o d   p x^2\equiv n \bmod p x2≡nmodp的一个方法
对 p p p进行分类讨论:
- p = 2 p=2 p=2 ,则 x = n x=n x=n
- p p p为奇素数
勒让德符号:
( a p ) = { 1 a 在 模 p 意 义 下 是 二 次 剩 余 − 1 a 在 模 p 意 义 下 是 非 二 次 剩 余 0 a ≡ 0   m o d   p \begin{pmatrix}\frac{a}{p}\end{pmatrix}=\begin{cases}1&a在模p意义下是二次剩余\\-1&a在模p意义下是非二次剩余\\0&a\equiv 0\bmod p\end{cases} (pa)=⎩⎪⎨⎪⎧1−10a在模p意义下是二次剩余a在模p意义下是非二次剩余a≡0modp
有一个定理: ( a p ) ≡ a p − 1 2   m o d   p \begin{pmatrix}\frac{a}{p}\end{pmatrix}\equiv a^{\frac{p-1}{2}}\bmod p (pa)≡a2p−1modp
证明:
若 a a a在模 p p p意义下是二次剩余,设 x 2 ≡ a   m o d   p x^2\equiv a\bmod p x2≡amodp,则有 x p − 1 ≡ 1   m o d   p x^{p-1}\equiv 1\bmod p xp−1≡1modp,由费马小定理显然成立
若 a a a在模 p p p意义下是非二次剩余,设 x 2 ≡ a   m o d   p x^2\equiv a\bmod p x2≡amodp,则有 x p − 1 ≡ − 1   m o d   p x^{p-1}\equiv -1\bmod p xp−1≡−1modp,由费马小定理显然不成立
若 a   m o d   p = 0 a\bmod p=0 amodp=0显然成立
所以可以首先判断是否有解,就用勒让德符号来判断
第二步需要找到一个 a a a,使得 w = a 2 − n w=a^2-n w=a2−n在模 p p p意义下是非二次剩余,
则 x = ( a + w ) p + 1 2 x=(a+\sqrt{w})^{\frac{p+1}{2}} x=(a+w)2p+1
证明:
定理: ( a + b ) p ≡ a p + b p   m o d   p (a+b)^p\equiv a^p+b^p \bmod p (a+b)p≡ap+bpmodp
证明:(其实可以感性理解,可以根据二项式定理展开,在中间的组合数的阶乘中, p p p无法被消掉,因此   m o d   p \bmod p modp一定为 0 0 0,有贡献的只有第一项和最后一项也就是 a p , b p a^p,b^p ap,bp
证明2:
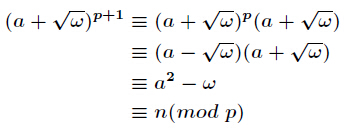
算法实现:因为大约有一半的数都是非二次剩余,所以可以随机一个 a a a,把 w \sqrt{w} w当作一个复数单位,定义一个复数运算
像这样:
struct F{int x,y;F(){}F(const int &xx,const int &yy){x=xx,y=yy;}
};inline F mul(F a,F b,int mod,int w){return F((1LL*a.x*b.x%mod+1LL*a.y*b.y%mod*w%mod)%mod,(1LL*a.x*b.y%mod+1LL*a.y*b.x%mod)%mod);
}
例题:模板题
代码如下:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<cstdlib>
#include<ctime>
#define LL long long
using namespace std;inline int rd(){int x=0,f=1;char c=getchar();while(c<'0' || c>'9') f=c=='-'?-1:1,c=getchar();while(c<='9' && c>='0') x=x*10+c-'0',c=getchar();return x*f;
}int t,a,n;struct F{int x,y;F(){}F(const int &xx,const int &yy){x=xx,y=yy;}
};inline F mul(F a,F b,int mod,int w){return F((1LL*a.x*b.x%mod+1LL*a.y*b.y%mod*w%mod)%mod,(1LL*a.x*b.y%mod+1LL*a.y*b.x%mod)%mod);
}inline F qpow(F x,int k,int mod,int w){F ret(1,0);while(k){if(k&1) ret=mul(ret,x,mod,w);x=mul(x,x,mod,w); k>>=1;} return ret;
}inline int Qpow(int x,int k,int mod){int ret=1;while(k){if(k&1) ret=1LL*ret*x%mod;x=1LL*x*x%mod; k>>=1;} return ret%mod;
}inline int solve(int n,int mod){if(mod==2) return 1;if(Qpow(n,(mod-1)>>1,mod)==mod-1) return -1;while(1){int a=rand()%mod;int w=(1LL*a*a%mod+mod-n)%mod;if(Qpow(w,(mod-1)>>1,mod)==mod-1){F ans=qpow(F(a,1),(mod+1)>>1,mod,w);return ans.x;}}
}int main(){scanf("%d",&t);while(t--){scanf("%d%d",&a,&n); a%=n;int ans=solve(a,n);if(ans==-1) puts("No root");else{int ans2=n-ans;if(ans>ans2) swap(ans,ans2);if(ans==ans2) printf("%d\n",ans);else printf("%d %d\n",ans,ans2);}}return 0;
}
- p p p为奇素数的幂
这里参考了这个博客
求解 x 2 ≡ a   m o d   p n x^2\equiv a\bmod p^n x2≡amodpn, g c d ( n , p ) = 1 gcd(n,p)=1 gcd(n,p)=1,下面只介绍方法
先求出方程 x 2 ≡ a   m o d   p x^2\equiv a\bmod p x2≡amodp的一个解 r r r,那么进一步有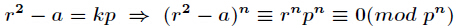
我们知道
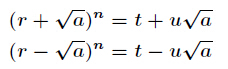
也就是
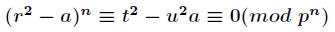
可证明 g c d ( t , p ) = 1 , g c d ( u , p ) = 1 gcd(t,p)=1,gcd(u,p)=1 gcd(t,p)=1,gcd(u,p)=1,最终得到
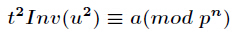
这里由于 p n p^n pn不是素数,所以求逆元用扩展欧几里得算法即可。 - p p p为合数
将 p p p质因数分解,问题变成了 3 3 3中的内容,然后解出各答案用中国剩余定理合并即可。