元胞自动机
元胞自动机( Cellular Automata) 是 20 世纪 50 年代初由计算机之父冯·诺依曼为了模拟生命系统所具有的自复制功能而提出来的网格动力学模型。
概念
元胞自动机采用离散的空间布局和离散的时间间隔,将元胞分成有限种状态,元胞个体状态的演变仅与其当前状态以及其某个局部邻域的状态有关。
将所有元胞自动机的动力学行为归纳为四大类(Wolfram. S.,1986):
⑴ 平稳型:自任何初始状态开始,经过一定时间运行后,元胞空间趋于一个空间平稳的构形,这里空间平稳即指每一个元胞处于固定状态。不随时间变化而变化。
⑵ 周期型:经过一定时间运行后,元胞空间趋于一系列简单的固定结构(Stable Patterns)或周期结构(Perlodical Patterns)。由于这些结构可看作是一种滤波器(Filter),故可应用到图像处理的研究中。
⑶ 混沌型:自任何初始状态开始,经过一定时间运行后,元胞自动机表现出混沌的非周期行为,所生成的结构的统计特征不再变止,通常表现为分形分维特征。
⑷ 复杂型:出现复杂的局部结构,或者说是局部的混沌,其中有些会不断地传播。
初等元胞自动机( Elementary Cellular Automata, ECA)的基本要素如下:
- 元胞空间:元胞在空间分布的空间格点的集合,如一维直线上等间距的点。可为某区间上的整数点的集合。二维的元胞自动机通常有三种划分方式(三角形、正方形、正六边形)
| 网格类型 | 优点 | 缺点 |
|---|---|---|
| 三角形 | 拥有相对较少的邻居数目,易于处理复杂边界 | 在计算机的表达与显示不方便,需要转换为四方网格 |
| 正方形 | 直观简单,而且适合于在现有计算机环境下进行表达显示 | 不能较好地模拟各向同性的现象 |
| 正六边形 | 能够较好地模拟各向同性的现象,因此,模型更更加自然而真实 | 在表达显示上较为困难、复杂 |
元胞空间的边界条件
理论上,元胞空间是无限的,实际应用中无法达到这一理想条件。常用的边界条件有以下几种:周期型、定值型、绝热型、反射型
-
周期型边界条件(Periodic Boundary)
是指相对边界连接起来的元胞空间,对于一维空间,首尾相接形成一个圆环;
对于二维空间,上下相接、左右相接,形成一个拓扑圆环面,形似车胎

-
定值型边界条件(Constant Boundary)
所有边界外元胞均取某一固定常量

-
绝热型边界条件(Adiabatic Boundary)
在指边界外邻居元胞的状态始终和边界元胞的状态保持一致,即具有状态的零梯度。
-
反射型边界条件(Constant Boundary)
在边界外邻居的元胞状态是以边界元胞为轴的镜面反射

- 状态集:S={s1,s2} 即只有两种不同的状态。这两种不同的状态可将其分别编码为0 与 1;若用图形表示,则可对应“黑”与“白” 或者其他两种不同的颜色。
- 邻居:若一维邻居半径r=1,即每个元胞最多只有“左邻右舍”两个邻居。
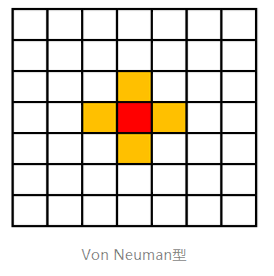
- 冯诺依曼型
邻居数目=2d
2. 摩尔型
邻居数目=3^d-1
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-zK0qkYQ5-1604564226207)(https://i.loli.net/2020/10/26/IO2TqoRk316LJpH.png)]
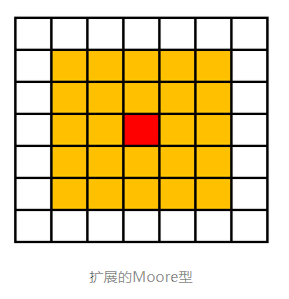
3. 扩展摩尔型
邻居数目=(2r+1)^d-1
4. 马格勒斯型(Margolus)
主要区别:以2*2的元胞块为单元进行处理,而不是单独处理
主要应用领域:格子气流体、颗粒流
- 演化规则:任意设定, 最多2^8=256种不同的设定方式。元胞以相邻的8个元胞为邻居。即Moore邻居;一个元胞的生死由其在该时刻本身的生死状态和周围八个邻居的状态决定。根据元胞及其邻居元胞的状态,决定下一时刻该元胞状态的动力学函数,也可以是状态转移方程或局部映射。
从数学上来定义,有限自动机是一个五元组:
FA=(Q,S,δ,q0,F)
其中,Q是控制器的有限状态集、S是输入符号约有限集、δ是控制状态转移规律的Q×S到Q的映射 (可用状态转移图或状态转移表表示),q0是初始状态、F是终止状态集。若δ是单值映射,则称M为确定性有限自动机;若δ是多值映射,则称M为非确定性 有限自动机。
特征
(1)同质性、齐性:同质性反映在元胞空间内的每个元胞都服从相同的规则;齐性指的是元胞的分布方式相同,大小形状相同,空间分布整齐。
(2)空间离散:元胞分布在按一定规则划分的离散的元胞空间上。
(3)时间离散:系统的演化是按等时间间隔分步进行的。t时刻的状态只对t+1时刻的状态产生影响。
(4)状态离散、有限:元胞自动机的状态参量只能取有限个离散值。
(5)同步计算(并行性):元胞自动机的处理是同步进行的。
(6)时空局域性:每个元胞在t+1时刻的状态,取决于其邻居的元胞在t时刻的状态。
(7)维数高:动力系统中一般将变量的个数成为维数。任何完备元胞自动机的元胞空间是在空间上的无穷集,每个元胞的状态是这个动力学系统的变量,因此元胞自动机是一类无穷维动力系统。
应用:
生物学领域
肿瘤细胞的增长机理和过程模拟
人类大脑的机理探索
艾滋病病毒HIV的感染过程
自组织、自繁殖等生命现象的研究
克隆技术
模拟植物的生长
贝壳上色素的沉积图案
生态学领域
生态系统动态变化过程的模拟
蚂蚁的行走路线,大雁、鱼类洄游动物的群体行为的模拟
生物群落的扩散模拟
物理学模拟
LGA 格子气自动机
LBM格子-玻尔兹曼法
流体领域,在多孔介质、多相流、微小尺寸具有独特的优越性
LBM同样被成功用于磁场、电场、热扩散、热传导的模拟
雪花等枝晶的形成
液态金属材料的凝固结晶过程
颗粒材料的垮塌现象
交通科学领域
两条主线:
1)Nagel-Schreckenberg模型
对城市道路交通流的研究
2)BML模型
对城市交通网络的研究
计算机科学与信息学领域
研究信息的保存、传递、扩散
图像处理和模式识别
184号模型
- 道路被划分为等距格子,每个格点表示一个元胞;
- 某个时刻,元胞或者是空的,或者被一辆车占据;
- 所有车辆的行进方向都是一致的(如向右);
- 在每一个时间步内:若第n辆车的前方元胞是空的,则该车可以向前行驶一步;
- 若前面的元胞被另一辆车n+1所占据,即使第n+1辆车在本时间步内离开此元胞,第n辆车也停在原地不动;
- 整个系统采用周期性边界条件以确保车辆数守恒。
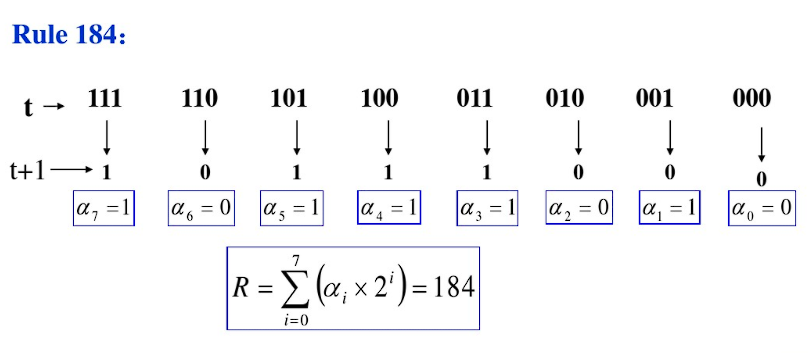
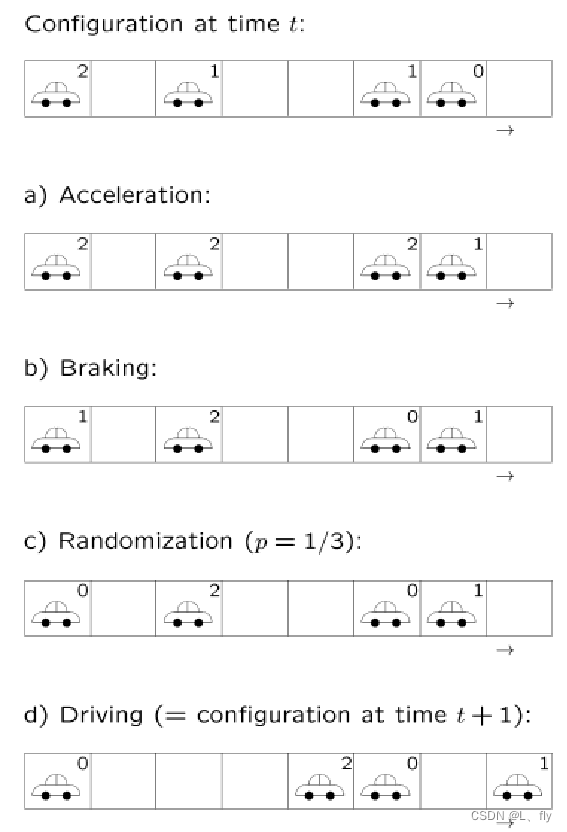
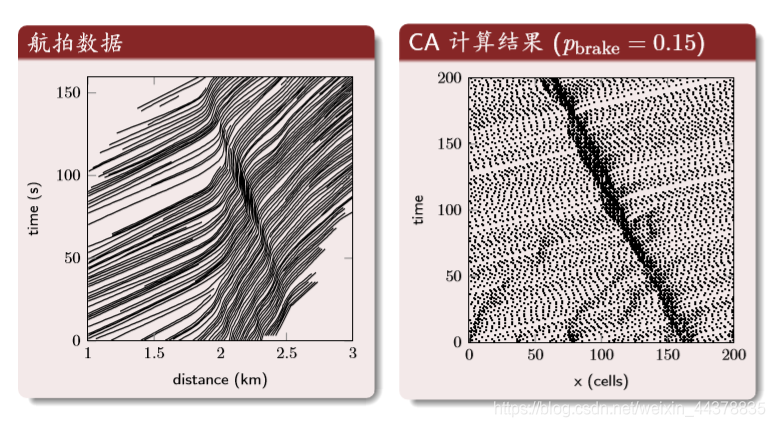
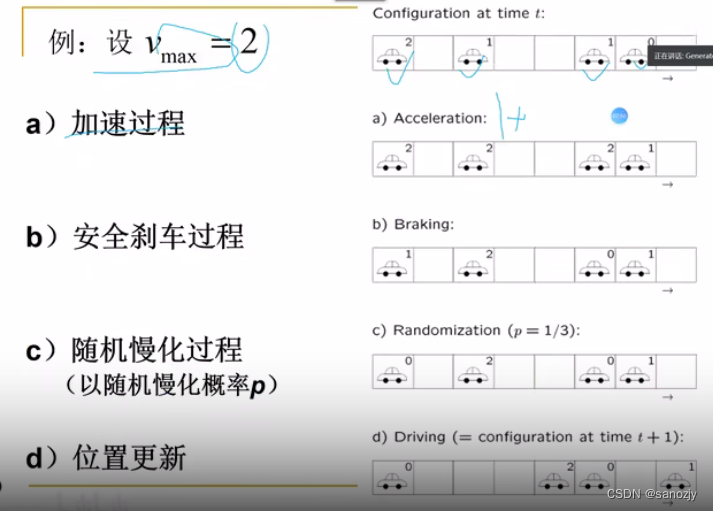
NaSch模型
NaSch模型是对184号模型的推广,1992年Nagle和Schreckenberg提出了著名的NaSch模型
Python 实现最简单的元胞自动机
选取的元胞状态只有两种,分别为 0 和 1。每一层由 64 个元胞组成,若元胞状态为 1,那么控制台将打印星号(*);如果元胞状态为 0,那么控制台将打印连字符(-)。也就是说,每一行由 64 个混合星号与连字符的图案组成。
状态更新规则:若当前元胞的前一个元胞的状态为 1,或者前一个元胞的左右两边的元胞的状态有且只有一个值为 1, 那么该元胞的状态就为 1。反之,元胞的状态设为 0。对于第一列和最后一列,我们只需分别考虑右元胞和左元胞即可。对于中间部分的元胞来说,若其领域元胞的状态为[0,1,0]、[0,0,1]、[1,0,0]、[1,1,0]等状态时,当前元胞的状态就为 1。
import time
def print_seq(seq, speed=0.5):for item in seq:if item:print('*', end='')else:print('-', end='')print('')time.sleep(speed)class Cell:def __init__(self, deepth=31):self.ca = [0 if i != 31 else 1 for i in range(64)]self.ca_new = []self.deepth = deepthdef process(self):print_seq(self.ca)for i in range(self.deepth):self._rule()print_seq(self.ca_new)self.ca = self.ca_newself.ca_new = []def _rule(self):for i in range(64):if 0 < i < 63:if self.ca[i - 1] == self.ca[i + 1]:self.ca_new.append(0)else:self.ca_new.append(1)elif i == 0:if self.ca[1]:self.ca_new.append(1)else:self.ca_new.append(0)else:if self.ca[62]:self.ca_new.append(1)else:self.ca_new.append(0)def main():cell = Cell()cell.process()if __name__ == '__main__':main()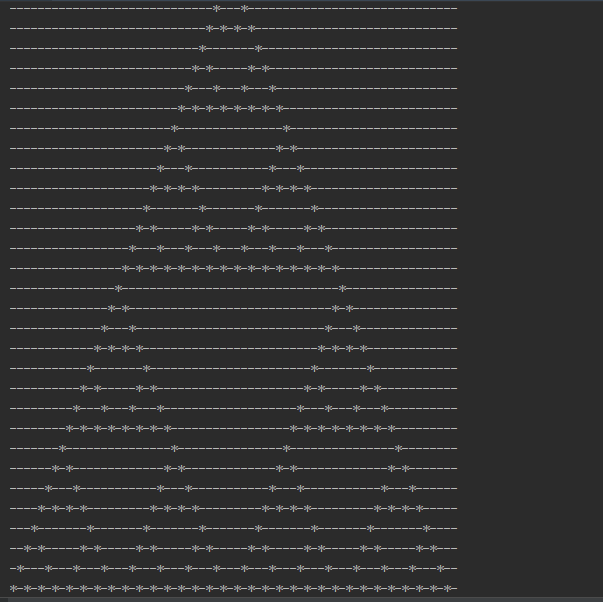
参考文章:
- 元胞自动机研究的相关理论方法