数据结构-第五章 二叉树

article/2025/9/20 3:11:58

一、树

1.树的概念

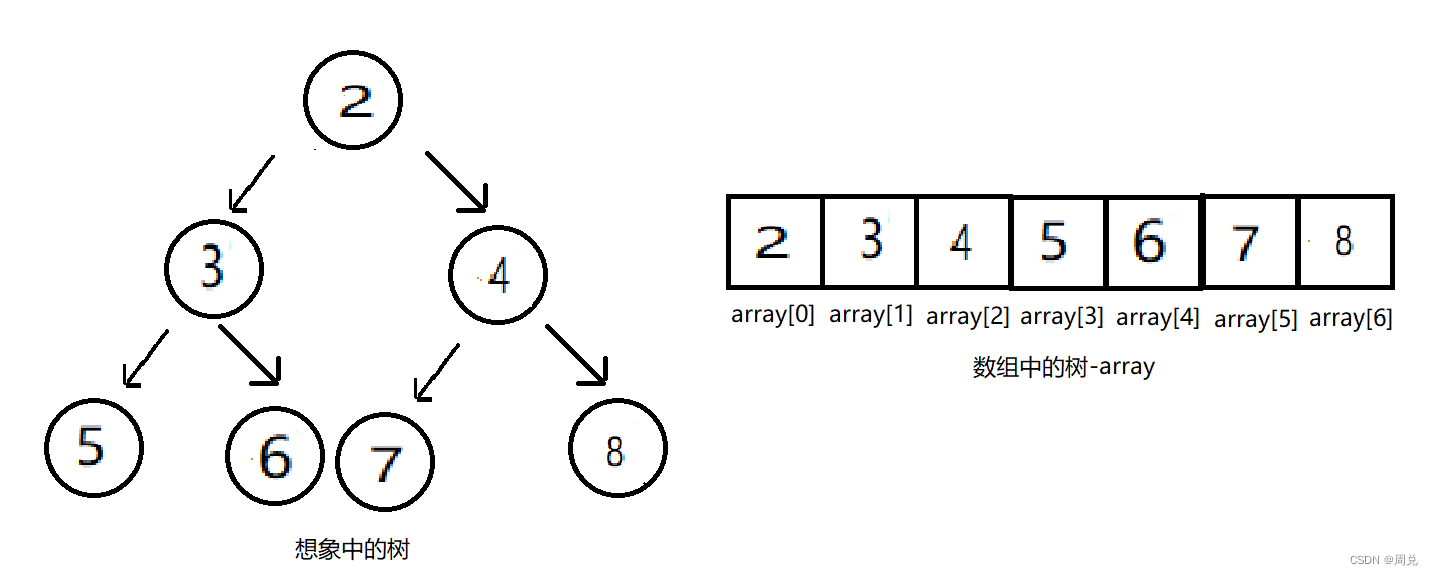
树是一种非线性的数据结构，是由n个结点组成的一个集合。每一棵树都可以被分解为根节点和n棵子树构成(n>=0)

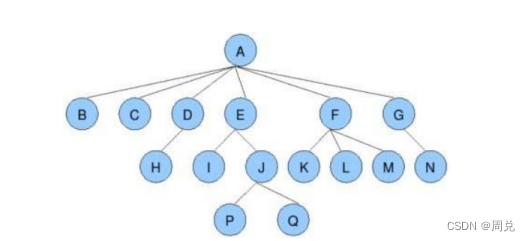
根节点(Root)：没有父结点的结点称为根节点，如A

父结点：含有子结点的结点，如A是B的父结点

子结点：含有父结点的结点，如B、C、D、E是A的子结点

子树：以自身节点为根节点，下面的所有子结点与子结点的子结点等，如B是A的子树，G、N也是A的子树、E、I、J、P、Q也是A的子树

叶节点：没有子节点的节点，如B、C、H、I、P、Q、K、L、M、N

兄弟结点：拥有同一个父结点的结点，如B、C、D、E、F、G是兄弟结点，I、J是兄弟结点

结点的度(子节点的个数)：树中父结点中，含有的子结点个数，如A的度是6，B的度是0，D的度是1，E的度是2

树的度：树中最大的结点的度就是树的度，该树的度是6

节点的层次：根节点的层次为第一层，根结点的子结点的层次为第二层，如E为第2层、Q为第4层

树的高度/深度：树中节点的最大层次，该树的深度是4

2.树的特征

1.子树是不相交的，即只有一条路线能找到子结点

2.除了根结点外，每个结点有且仅有一个父结点

3.一棵N个结点的树有N-1条边

二、二叉树

1.二叉树的概念

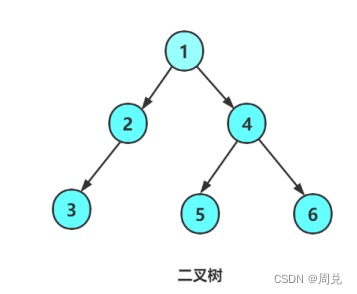
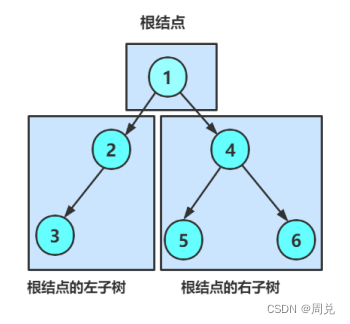
1.二叉树的度为2(一个父节点最多有两个子节点)

2.二叉树的子树有左右之分

2.二叉树的分类

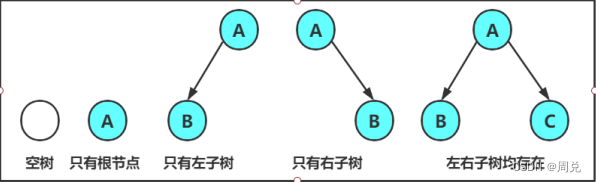
3.特殊的二叉树 

1.满二叉树-每一个父节点都有两个子节点，最后一层没有子节点

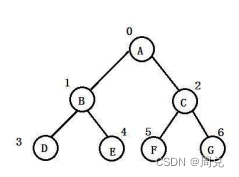
2.完全二叉树-前k-1层都是满的，最后一层不满或是满的，但最后一层从左到右是连续的。满二叉树是一个特殊的完全二叉树

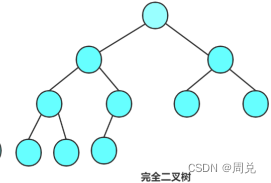
4.二叉树的性质

1.关于结点个数N-普通二叉树

规定根节点的层数为1

1.第n层上的节点个数N为：0≤N≤2^(n-1)

2.一个深度为n层的二叉树的节点个数N：n≤N≤2^n - 1

3.叶节点的个数为N0，度为1(有一个子节点)的节点的个数为N1，度为2(有两个子节点)的节点的个数为N2，则N0 = N2 + 1；N = N0 + N1 + N2；N = 2N2 + N1 + 1

2.关于结点个数N-完全二叉树

规定根节点的层数为1

1.第n层上的节点个数N为：0≤N≤2^(n-1)

2.一个深度为n层的完全二叉树的节点个数N：2^(n - 1)(上一层全满，最后一层有一个节点)≤N≤2^n - 1(满二叉树的节点数)

3.叶节点的个数为N0，度为1(有一个子节点)的节点的个数为N1，度为2(有两个子节点)的节点的个数为N2，则N0 = N2 + 1；N = N0 + N1 + N2；N = 2N2 + N1 + 1；且N1能且只能等于1或0

三、二叉树顺序结构及实现-堆(一个特殊的完全二叉树)

只有完全二叉树或是满二叉树时，才用数组实现，而在使用情况下，只有使用堆的时候才使用顺序结构

1.堆的概念及结构

1.堆是一个完全二叉树

2.堆分为小堆和大堆

小堆：根节点的值是堆中数据最小的，且小堆中任意父节点的值总是≤子节点的值

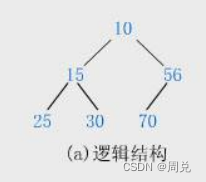
根节点的值为10，是最小的数值。且15≤25、30

大堆：根节点的值是堆中数据最大的，且大堆中任意父节点的值总是≥子节点的值

 

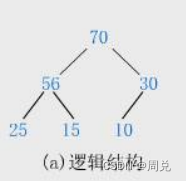
根节点的值为70，是最大的值。且56≥25、15 

2.堆的存储-以小堆为例

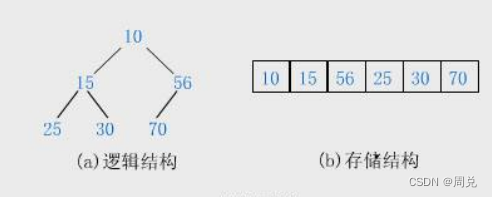
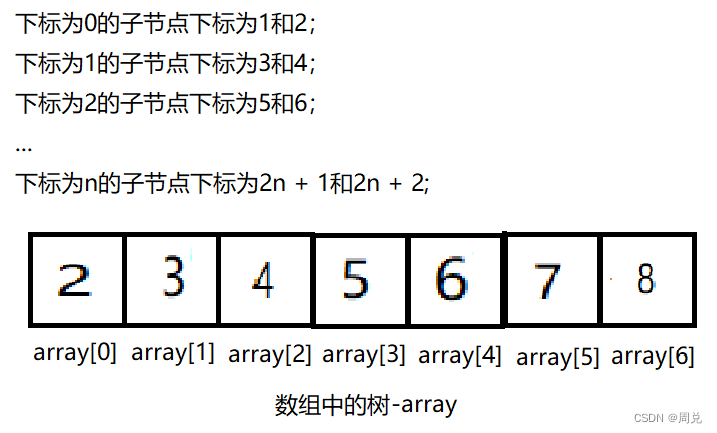
 一个堆按照从上到下，从左到右的顺序将数值存储进数组。

3.堆的实现-如何在一个数组中实现堆的结构

0.思想

先实现一个堆，然后一个一个数据加进数组，再进行调整，使之成为堆

1.向上调整法-用于从数组底插入数据

第一层

创建一个根节点，然后向数组中插入数据(假设数据为4)

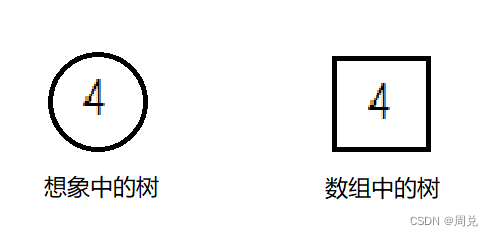
第二层

创建根节点的左子节点，然后向数组中插入数据(假设左子节点中的数据为5)

 

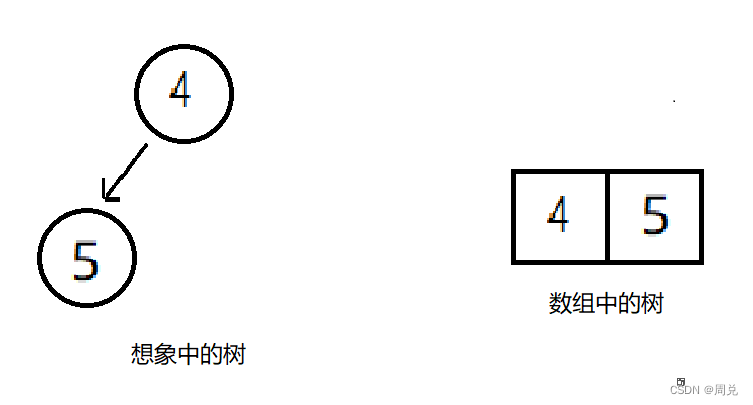
比较子节点与父结点的值，若子结点的值小于父结点，则进行对换(此处不兑换)。然后插入数据为3的右子节点

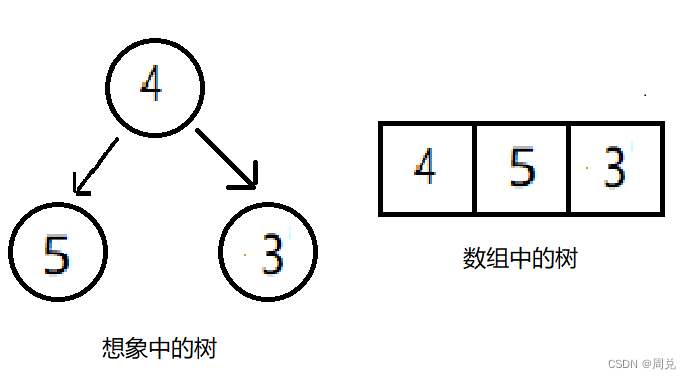
比较父结点与子节点的值，进行对换

 

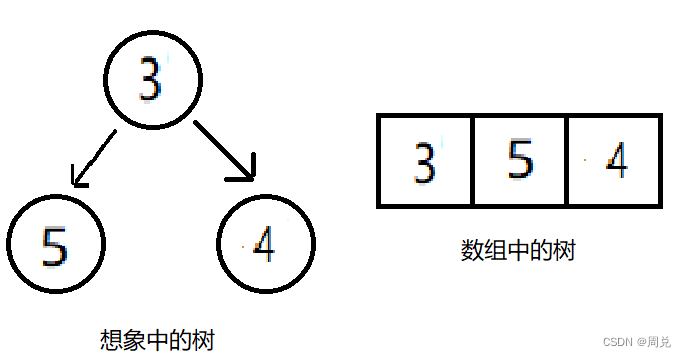
 第三层-插入值为2、6、7、1

插入2

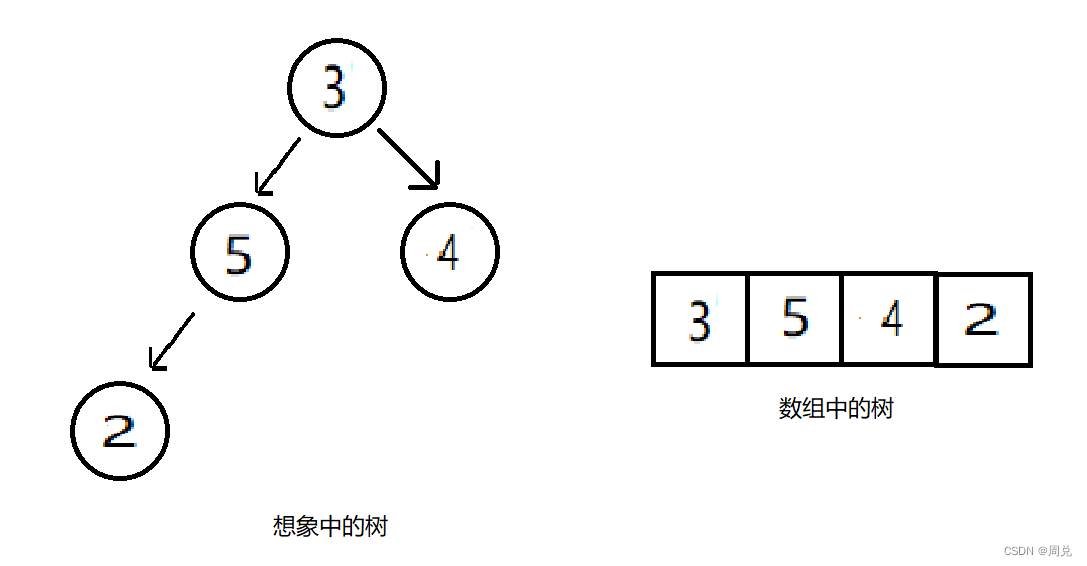
 调整：2与5换，然后2与3换

 

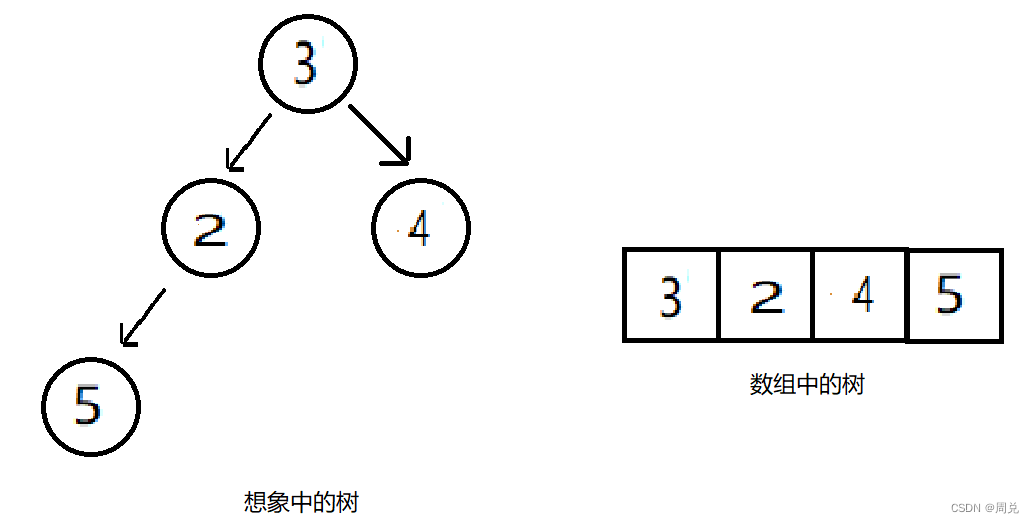
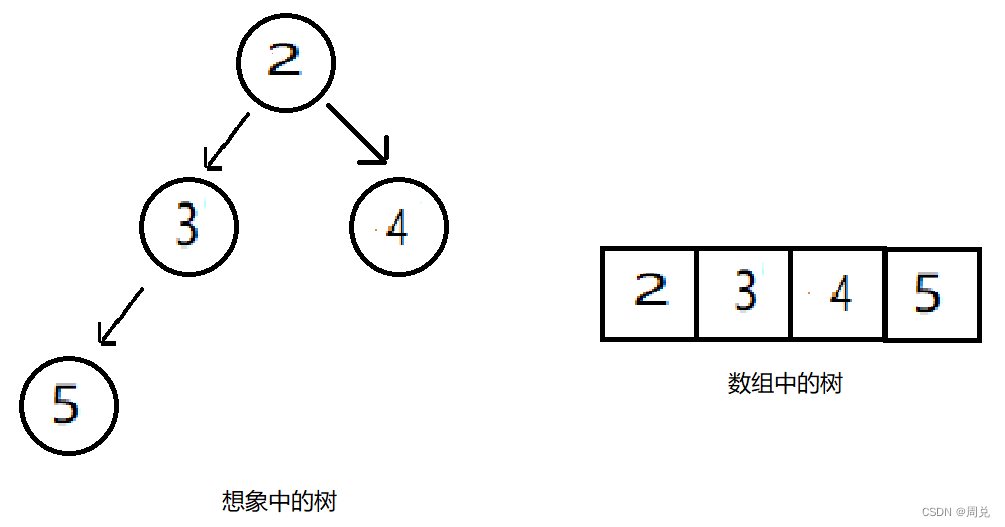
 插入6，不需要调整，插入7，不需要调整，最后插入1

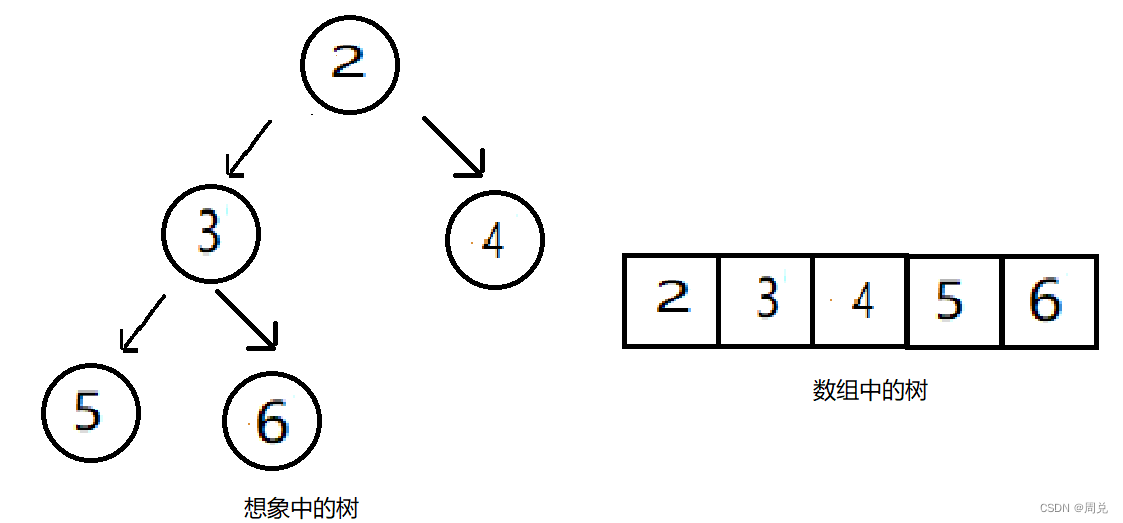
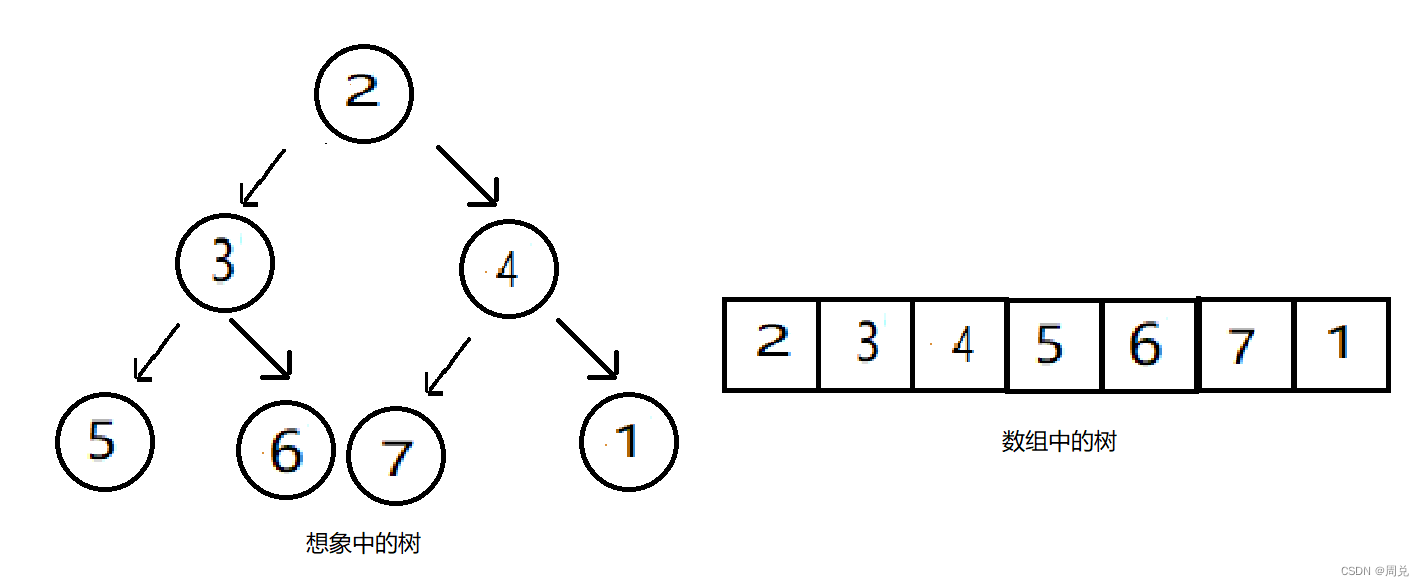
 对1进行调整，先与4换，再与2换

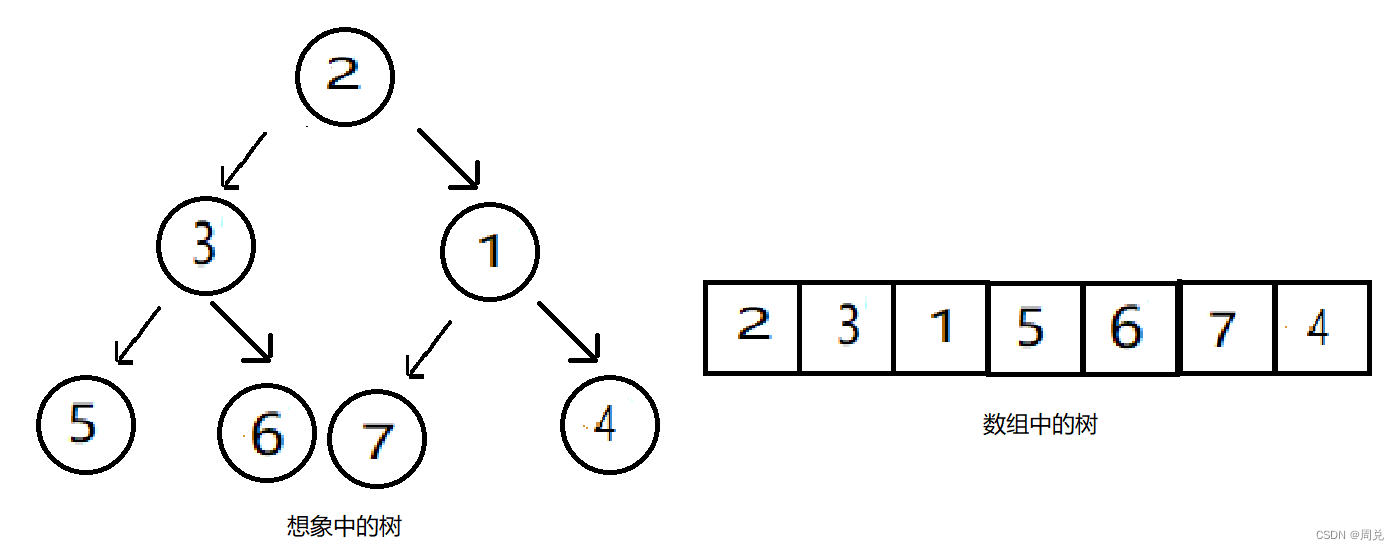
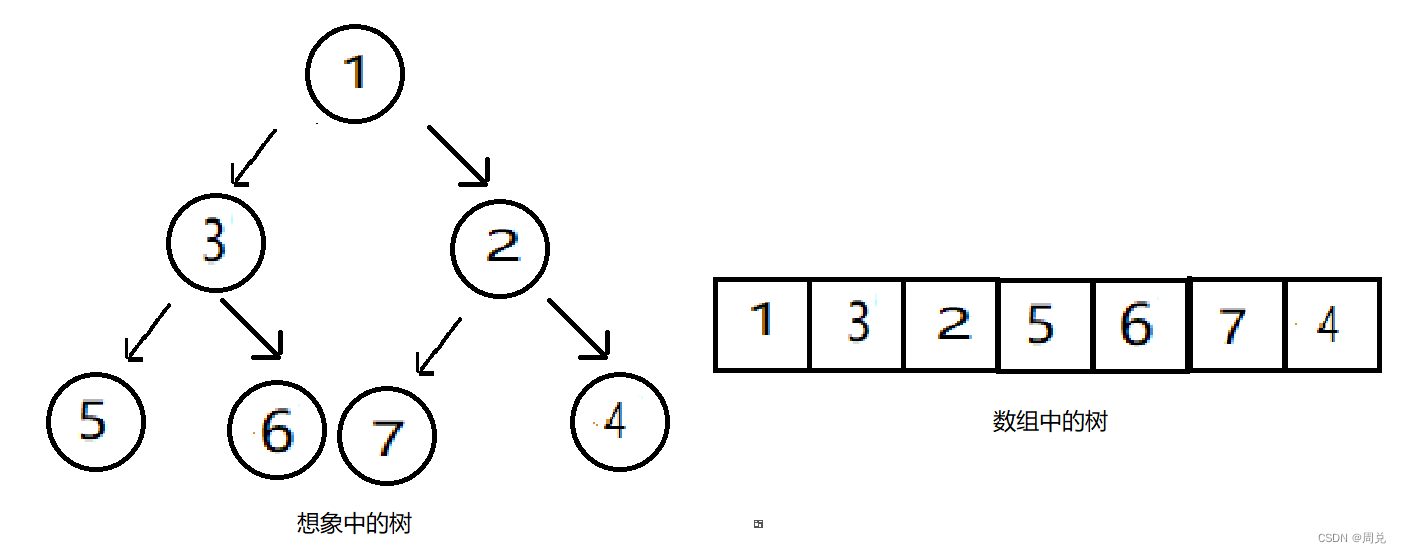
此时完成了全部数组的构建，即整个树的构建。

要点：

2.向下调整法-用于除了根节点外，其他的节点都已经是堆了

同上图，假设根节点为8

第零步、根节点中的值被替换为8

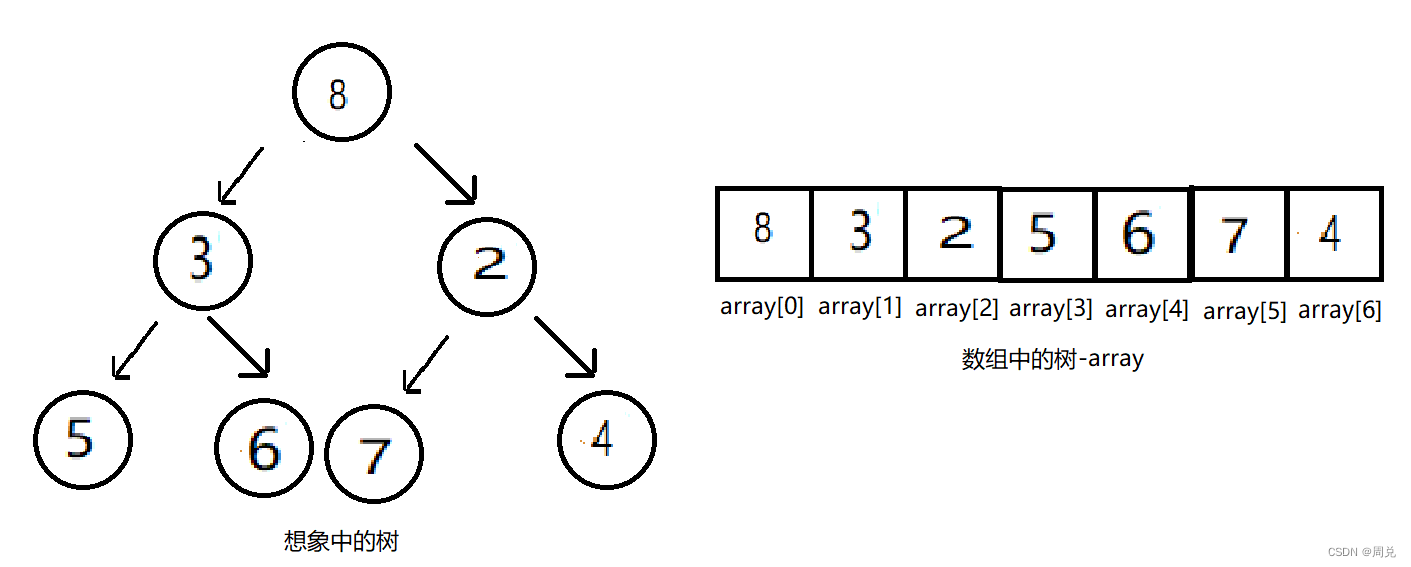
 第一步、找根节点的左右子结点中的最小值，如上图，最小值为2，与2替换

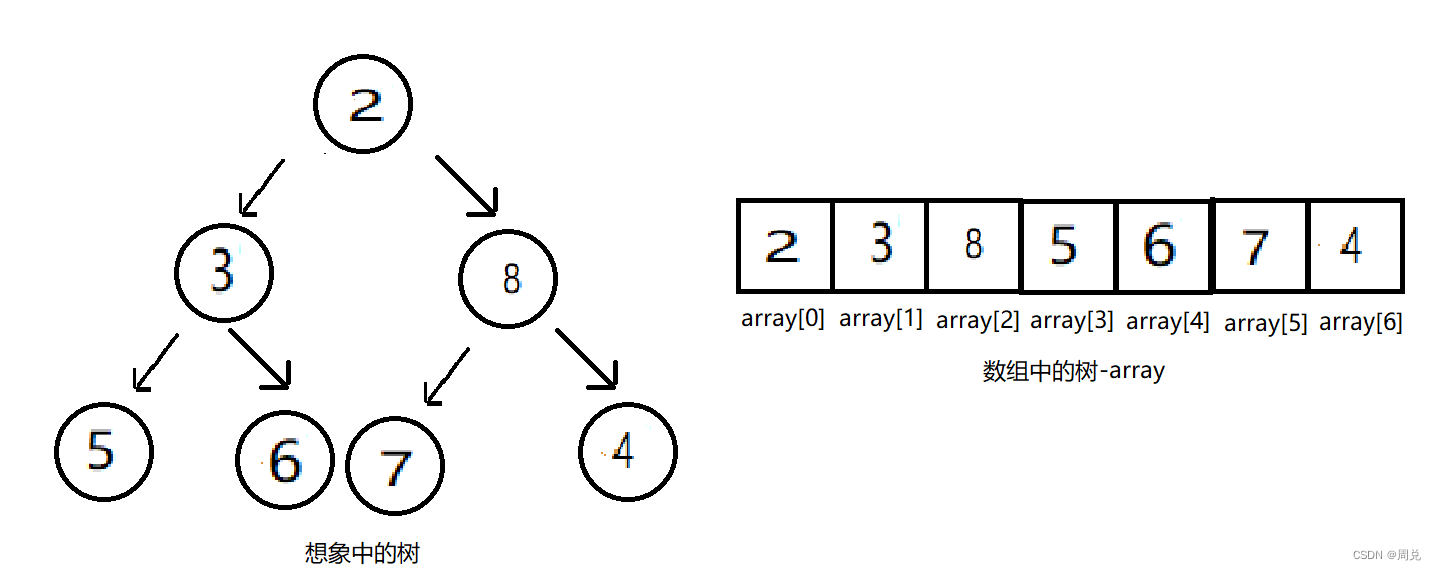
 第二步、以被替换的节点为父结点，再跟子结点进行比较，如上图，就是8跟4换

 同样要点为：

4.堆的代码实现

4.1堆结构的定义

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>#define _CRT_SECURE_NO_WARNINGS 1 //构建堆
//小堆-root根节点的值为整个堆中的最小值
//大堆-root根节点的值为整个堆中的最大值
typedef int HPDataType;//堆中存储的数据类型typedef struct Heap
{HPDataType* array;//以数组的形式来存储数据int size;//堆中的数据个数int capacity;//堆中的可存储数据的内存
}Heap;

4.2堆的初始化

//堆的构建-传入一个堆变量的地址
void HeapCreate(Heap* php)
{assert(php);php->array = NULL;php->size = 0;php->capacity = 0;
}

4.3堆的销毁

//堆的销毁-传入一个堆变量的地址
void HeapDestroy(Heap* php)
{assert(php);free(php->array);php->array = NULL;php->size = 0;php->capacity = 0;
}

4.4堆的打印

//堆的数据输出-传入一个堆变量的地址，打印出堆中的数据
void HeapPrint(Heap* php)
{assert(php);//1.堆中没有数据if (0 == php->size){printf("堆中没有数据，无法打印\n");}//2.堆中有数据else{for (int i = 0; i < php->size; i++){printf("%d  ", php->array[i]);}printf("\n");}
}

4.5堆的数据插入

4.5.0交换数据的函数实现

//交换数据-传入两个堆变量的数据的地址，使之交换数据
void Swap(HPDataType* pa, HPDataType* pb)
{assert(pa);assert(pb);HPDataType tmp = *pa;*pa = *pb;*pb = tmp;
}

4.5.1向上调整数据的实现

//堆的向上调整-传入一个数组的地址，需调整数据在数组中的下标
//本质是在数组是堆的基础上，调整新插入的数据，使数据插入后成为堆
void AdjustUp(HPDataType* array, int position)
{assert(array);int child = position;//可能为0int parent = (child - 1) / 2;//可能为负数//当该数据不为数组的首元素时，进入循环while (child){//1.若新插入的数据小于堆中已有的数据，进行交换if (array[child] < array[parent])//小堆的实现//if (array[child] > array[parent])//大堆的实现{Swap(&array[child], &array[parent]);child = parent;//可能为0parent = (child - 1) / 2;//可能为负数}//2.若新插入的数据大于等于堆中的数据，则满足堆的定义//无需交换，出循环else{break;}}//出循环，说明该堆已经调整好了
}

 4.5.2堆的数据插入

//堆的数据插入-传入一个堆变量的地址，一个数据
void HeapPush(Heap* php, HPDataType x)
{assert(php);//1.检查容量与扩容if (php->size == php->capacity){//定义新容量的大小int newcapacity;if (0 == php->capacity){newcapacity = 4;}else{newcapacity = php->capacity * 2;}//利用新容量来申请数组空间HPDataType* newarray = (HPDataType*)realloc(php->array, sizeof(HPDataType) * newcapacity);assert(newarray);//更新数组与容量php->array = newarray;php->capacity = newcapacity;}//2.插入数据php->array[php->size] = x;php->size++;//3.将插入的数据在数组中进行调整，使数组是一个堆AdjustUp(php->array, php->size - 1);
}

4.6堆的数据删除

4.6.1堆的向下调整

//堆的向下调整-传入一个数组的地址，该数组中含有的数据个数
//本质上是数组除了堆顶数据外，是一个堆结构
//调整堆顶数据使之成为一个堆
void AdjustDown(HPDataType* array, int size)
{assert(array);//1.标识父结点与左子结点在数组中的下标int parent = 0;int child = parent * 2 + 1;//可能该下标在数组下标之外//2.当左子结点的数组下标在数组中时，进入循环while (child < size){//1.找出左右子结点中更小(小堆)/更大(大堆)的值if ((child + 1 < size) && array[child + 1] < array[child])//小堆的调整//if((child + 1 < size) && array[child + 1] > array[child])//大堆的调整{child = child + 1;}//2.比较父结点与子结点的值if (array[child] < array[parent])//小堆的实现//if (array[child] > array[parent])//大堆的实现{Swap(&array[child], &array[parent]);parent = child;//此时parent的下标必在数组下标中child = parent * 2 + 1;//此时child的下标不一定在数组下标中}//3.若父结点满足堆的定义，则直接退出循环else{break;}}//3.出循环，说明调整完成，此时数组的结构为堆
}

4.6.2堆的数据删除

//堆的数据删除-传入一个堆变量的地址
void HeapPop(Heap* php)
{assert(php);//传入一个没有数据的堆if (0 == php->size){printf("堆中没有数据，无法删除\n");}//传入一个有数据的堆else{//1.交换堆顶和堆底的数据Swap(&php->array[0], &php->array[php->size - 1]);//2.删除堆底的数据php->size--;//3.调整数组的结构，使之成为一个堆AdjustDown(php->array, php->size);}}

4.7输出堆的堆顶元素

//堆顶的数据-传入一个堆变量的地址，输出堆变量中堆顶的数据
HPDataType HeapTop(Heap* php)
{assert(php);assert(php->size);return php->array[0];
}

4,8输出堆的数据个数

//堆的数据个数-传入一个堆变量的地址，输出堆变量中数据的个数
int HeapSize(Heap* php)
{assert(php);return php->size;
}

4.9判断堆是否是空堆

//堆是否为空-传入一个堆变量的地址，该堆中没有数据，返回1，否则返回0
int HeapEmpty(Heap* php)
{assert(php);return 0 == php->size;
}

四、二叉树链式结构及实现-普通的二叉树

0.二叉树的结构体定义

typedef char BTDataType;typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;

1.通过前序遍历的数组"ABD##E#H##CF##G##"来构建二叉树

//通过前序遍历的数组"ABD##E#H##CF##G##"来构建二叉树
//传入一个保存数据的数组的地址，传入该数组的元素个数，
//传入记录数组下标的整数地址
BTNode* BinaryTreeCreate(BTDataType* array, int n, int* pi)
{assert(array);assert(*pi < n);//要求记录数组下标 的 整数<数组中的元素个数//1.该数值是'#',返回空if ('#' == array[*pi]){*pi = *pi + 1;return NULL;}//2.该数值不为'#'else{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));assert(newnode);newnode->data = array[*pi];*pi = *pi + 1;newnode->left = BinaryTreeCreate(array, n, pi);newnode->right = BinaryTreeCreate(array, n, pi);return newnode;}
}

2.二叉树销毁

//二叉树销毁-前序销毁
void BinaryTreeDestroy(BTNode** root)
{assert(root);//1.该指针变量中存的是空地址if (NULL == *root){return;}//2.该指针变量中存的是某个节点的地址BTNode* parent = *root;BTNode* left = parent->left;BTNode* right = parent->right;free(parent);parent = NULL;*root = NULL;BinaryTreeDestroy(&left);BinaryTreeDestroy(&right);
}

3.二叉树的节点个数

//二叉树节点个数
int BinaryTreeSize(BTNode* root)
{//1.传入的是空树if (NULL == root){return 0;}//2.传入的是非空树return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}

4.二叉树叶子节点个数

//二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{//1.传入的是空树if (NULL == root){return 0;}//2.传入的是非空树if (NULL == root->left && NULL == root->right){return 1;}else{int i_left = BinaryTreeLeafSize(root->left);int i_right = BinaryTreeLeafSize(root->right);return i_left + i_right;}
}

5.二叉树第k层节点个数

//二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{assert(k);//要求k为大于0的一个数，定义根节点为第一层//1.当这一层是第k层时(当k=1时，是根节点那一层)if (1 == k){//1.是空节点if (NULL == root){return 0;}//2.不是空节点else{return 1;}}//2.当这一层不是第k层时else{//1.是空节点if (NULL == root){return 0;}//2.不是空节点，是叶子节点if (NULL == root->left && NULL == root->right){return 0;}//3.不是空节点也不是叶子节点return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);}
}

6.二叉树查找值为x的节点

//二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{//1.该节点为空节点if (NULL == root){return NULL;}//2.该节点有值且等于要找的值if (x == root->data){return root;}//3.该节点有值但不等于要找的值BTNode* left = BinaryTreeFind(root->left, x);if (left)//左边找到了{return left;}BTNode* right = BinaryTreeFind(root->right, x);if (right)//右边找到了{return right;}return NULL;
}

7.二叉树前序遍历

//二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{//1.空节点if (NULL == root){printf("NULL ");return;}//2.非空节点printf("%c ", root->data);BinaryTreePrevOrder(root->left);BinaryTreePrevOrder(root->right);
}

8.二叉树中序遍历

//二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{//1.空节点if (NULL == root){printf("NULL ");return;}//2.非空节点BinaryTreeInOrder(root->left);printf("%c ", root->data);BinaryTreeInOrder(root->right);
}

9.二叉树后序遍历

//二叉树后续遍历
void BinaryTreePostOrder(BTNode* root)
{//1.空节点if (NULL == root){printf("NULL ");return;}//2.非空节点BinaryTreePostOrder(root->left);BinaryTreePostOrder(root->right);printf("%c ", root->data);
}

10.二叉树层序遍历

typedef BTNode* QueueDataType;typedef struct QueueNode
{QueueDataType data;struct QueueNode* next;
}QueueNode;typedef struct Queue
{QueueNode* front;QueueNode* tail;
}Queue;//创造一个队列的节点-使用方法：QueueNode* newnode = BuyNode(x);
QueueNode* BuyNode(QueueDataType x)
{QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));assert(newnode);newnode->data = x;newnode->next = NULL;return newnode;
}//创造一个队列-使用方法：Queue* newqueue = QueueCreate();
Queue* QueueCreate()
{Queue* newqueue = (Queue*)malloc(sizeof(Queue));assert(newqueue);newqueue->front = NULL;newqueue->tail = NULL;return newqueue;
}//销毁一个队列-使用方法：QueueDestroy(&newqueue);
void QueueDestroy(Queue** sq)
{assert(sq);//1.队列中没有数据if (NULL == (*sq)->front){free(*sq);*sq = NULL;}//2.队列中有数据else{QueueNode* current = (*sq)->front;while (current){QueueNode* next = current->next;free(current);current = next;}free(*sq);*sq = NULL;}
}//向队列中插入数据-使用方法：QueuePush(newqueue,x);
void QueuePush(Queue* sq, QueueDataType x)
{assert(sq);//1.该队列中没有数据if (NULL == sq->front){sq->front = BuyNode(x);sq->tail = sq->front;}//2.该队列中有数据else{QueueNode* newnode = BuyNode(x);sq->tail->next = newnode;sq->tail = sq->tail->next;newnode = NULL;}
}//删除队列中的队头节点，并返回队头的数据-使用方法：QueuePop(newqueue);
QueueDataType QueuePop(Queue* sq)
{assert(sq);QueueDataType data = sq->front->data;QueueNode* current = sq->front;//1.该队列只有一个数据if (sq->front == sq->tail){free(current);current = NULL;sq->front = NULL;sq->tail = NULL;}//2.该队列有多个数据else{sq->front = sq->front->next;free(current);current = NULL;}return data;
}//二叉树层序遍历-依靠队列实现
void BinaryTreeLevelOrder_Queue(Queue* sq)
{assert(sq);//1.队列中没有数据if (NULL == sq->front){return;//队列中没有数据，退出}//2.队列中有数据else{BTNode* current = QueuePop(sq);//拿出队列中队头的元素，此时队列变成了空队列//1.拿出的根节点为空if (NULL == current){printf("NULL ");BinaryTreeLevelOrder_Queue(sq);//继续拿下一个元素}//2.拿出的根节点不为空else{printf("%c ", current->data);//输出根节点中的值QueuePush(sq, current->left);//左子节点的值入队列QueuePush(sq, current->right);//右子节点的值入队列BinaryTreeLevelOrder_Queue(sq);//继续拿下一个元素}}
}//二叉树层序遍历-依靠队列实现
void BinaryTreeLevelOrder(BTNode* root)
{//1.输入的是一个空树if (NULL == root){printf("NULL ");return;}//2.输入的是一个非空树Queue* newqueue = QueueCreate();QueuePush(newqueue, root);//把根节点的地址存入队列BinaryTreeLevelOrder_Queue(newqueue);//通过队列来输出二叉树//队列中已经有一个数据printf("\n");//输出了二叉树的全部元素，输出一个换行QueueDestroy(&newqueue);//销毁队列
}

11.判断二叉树是否是镜像二叉树

//判断两个子树是否镜像对称
int BinaryTreeisComplete(BTNode* left, BTNode* right)
{//1.两个子树都为空if (NULL == left && NULL == right){return 1;}//2.两个子树中有一个为非空if (NULL == left || NULL == right){return 0;}//3.两个子树都不为空，且值相等if (left->data == right->data){return BinaryTreeisComplete(left->right, right->left) && BinaryTreeisComplete(left->left, right->right);}//4.两个子树都不为空，且值不相等return 0;
}//判断二叉树是否是完全二叉树，是则返回1，不是则返回2
int BinaryTreeComplete(BTNode* root)
{//1.传入的是空树if (NULL == root){return 1;}//2.传入的是非空树return BinaryTreeisComplete(root->left, root->right);
}


http://chatgpt.dhexx.cn/article/t3lNPb61.shtml

相关文章

零基础学二叉树

零基础学二叉树

目录 二叉树的定义&#xff1a; 二叉树的应用&#xff1a; 认识二叉树&#xff1a; 二叉树的基本形式&#xff1a; 二叉树的节点&#xff1a; 二叉树的高度和深度&#xff1a; 二叉树的子树&#xff1a; 二叉树的度&#xff1a; 满二叉树&#xff1a; 完全二叉树&…
阅读更多...
npm 升级

npm 升级

npm 版本升级 mac版本 npm install -g npm1.网上有看到别的同学碰到升级报错的情况&#xff1a;可以试试用管理员身份安装&#xff1a; sudo npm install -g npm windows版本 npm install -g npm2.安装完成之后&#xff0c;输入npm -v检查是否升级成功&#xff0c;我是从6.…
阅读更多...
npm升级到最新版本

npm升级到最新版本

阅读更多...
npm 升级依赖包

npm 升级依赖包

首先安装升级插件 npm-check-updates $ npm install -g npm-check-updates # 或者 $ cnpm install -g npm-check-updates ncu 是 npm-check-updates 的缩写命令 输入ncu命令&#xff0c;可以看到需要升级安装包 # 查看更新ncu 可以看到有好几个包要更新 # 查看所有ncu命令…
阅读更多...
npm升级自身版本

npm升级自身版本

查看版本&#xff1a;npm -v 查看版本详情&#xff1a;npm version 用命令npm view npm version&#xff0c;运行后会输出到目前为止npm的所有版本&#xff0c;如图&#xff1a; 升级为特定的版本&#xff0c;命令:npm -g install npm4.0.2,运行后并检验版本如图&#xff1a;…
阅读更多...
npm 升级后，无法运行

npm 升级后，无法运行

更新npm npm install -g npm9.2.0问题&#xff1a;无法加载文件 D:\Program Files\nodejs\npm.ps1&#xff0c;因为在此系统上禁止运行脚本。 解决&#xff1a;依次输入如下命令 get-ExecutionPolicySet-ExecutionPolicy -Scope CurrentUserRemoteSignedget-ExecutionPolicy…
阅读更多...
npm升级

npm升级

啥时候升级&#xff1f; 在使用npm安装依赖包&#xff0c;终端出现以下提示 New major version of npm available! 6.13.4 -> 8.5.5 Changelog: https://github.com/npm/cli/releases/tag/v8.5.5 Run npm install -g npm to update! 如何升级 npm install npm -g升级报…
阅读更多...
npm升级导致npm报错

npm升级导致npm报错

文章目录 问题解决其他 问题 事情起因在于&#xff0c;我在执行npm init -y的时候&#xff0c;提示我可以升级 好家伙&#xff0c;脑子一时不清醒&#xff0c;我就执行了。以前看到都没想过要执行&#xff0c;今天不知道怎么了&#xff0c;也许是早饭吃多了撑的 : ) 执行完之…
阅读更多...
npm 升级遇到的问题

npm 升级遇到的问题

问题&#xff1a;在VUE项目中&#xff0c;当前的npm版本有点低&#xff0c;想对npm进行升级&#xff0c;将npm从6.14.13的版本升级到8.0.0版本&#xff0c;运行npm install -g npm8.0.0报错 解决方法&#xff1a; 找到node文件夹下面的npm.cmd&#xff0c;将它重命名为npmx.cm…
阅读更多...
npm 升级node.js

npm 升级node.js

升级NPM 到最新 查看npm 版本&#xff1a; npm -v 更新到最新版本&#xff1a; npm install npmlatest -g 升级Node.js 从node官网下载最新node.js 安装包覆盖原理的node.js 最新node.js 下载 winr cmd 输入 where node 查看原来node 安装路径 安装成功后查看node 版本
阅读更多...
如何升级npm 和 安装nvm 及 升级node.js

如何升级npm 和 安装nvm 及 升级node.js

1.NPM如何升级&#xff1f; 1.1.可以使用NPM自带的命令进行升级&#xff1a; npm install -g npm 注&#xff1a;这个命令会安装最新的&#xff0c;安装到全局。 2.查看NPM版本 npm -v 注&#xff1a;要是版本过低&#xff0c;可使用上面所说命令进行升级。 3.怎么把node.js升…
阅读更多...
国外的凹凸函数定义（简单粗暴）

国外的凹凸函数定义（简单粗暴）

阅读更多...
算法优化（1）：基础知识-凸集，单峰函数，拟凸函数与凸函数，函数凹凸性定义

算法优化（1）：基础知识-凸集，单峰函数，拟凸函数与凸函数，函数凹凸性定义

本文笔记介绍我最近学习的算法优化的基础知识&#xff0c;有&#xff1a; 最优化问题的一般形式约束问题的分类及形式优化问题的分类单峰函数&#xff08;Unimodal function&#xff09;的定义拟凸函数&#xff08;Quasiconvex function&#xff09;的定义凸集&#xff08;conv…
阅读更多...
deep_learning_凹凸函数

deep_learning_凹凸函数

什么是凸函数及如何判断一个函数是否是凸函数 t元j 一、什么是凸函数 对于一元函数f(xf(x)&#xff0c;如果对于任意tϵ[0,1]tϵ[0,1]均满足&#xff1a;f(tx1(1−t)x2)≤tf(x1)(1−t)f(x2)f(tx1(1−t)x2)≤tf(x1)(1−t)f(x2)&#xff0c;则称f(x)f(x)为凸函数(convex function…
阅读更多...
凹凸函数的图像值的深入

凹凸函数的图像值的深入

参考来源参考
阅读更多...
德.摩根定律及其理解

德.摩根定律及其理解

德.摩根定律的定义如下&#xff1a; 文字描述如下&#xff1a; 使用对偶性可以很方便的记忆和使用这个定律。. 我们知道如下关系呈现对偶关系&#xff0c;可以认为是“非”的关系&#xff1a; 那么将 利用对偶关系对应改写可以得到&#xff1a; .那么可以对应得到&#xff1a;…
阅读更多...
[产品07]-产品设计定律-菲茨定律/席克定律

[产品07]-产品设计定律-菲茨定律/席克定律

[产品07]-产品设计定律-菲茨定律/席克定律 一、菲茨定律1-1定义1-2应用场景1-3菲茨定律启示 二、席克定律2-1定义2-2作用 一、菲茨定律 1-1定义 菲茨定律所提出的人机界面设计法则&#xff0c;主页定义了游标移动到目标之间的距离&#xff0c;目标的大小和所花费的时间之间的…
阅读更多...
需求定律的4个准则——《可以量化的…

需求定律的4个准则——《可以量化的…

5.1.5 需求定律的4个准则 需求定律有4个准则&#xff1a;价值决定价格基准&#xff0c;竞争决定价格波动幅度。消费者盈余决定购买量&#xff0c;价格决定消费者的最低层次。 1&#xff09;价值决定价格基准 消费者购买产品是为了获得商品所带来的价值&#xff0c;商品能带来的…
阅读更多...
摩尔定律即将走向终结？对未来更广阔世界影响的55个预测！

摩尔定律即将走向终结？对未来更广阔世界影响的55个预测！

Datawhale干货 译者&#xff1a;罗泽铭&#xff0c;伦敦大学城市学院 原文&#xff1a;https://bzogrammer.substack.com/p/the-next-century-of-computing 原作&#xff1a;Charles Rosenbauer&#xff0c;审校&#xff1a;肖明远 在这篇文章中&#xff0c;我将对信息处理技术…
阅读更多...
需求分析的概念和原则

需求分析的概念和原则

概念和原则 需求分析是指在软件开发和项目管理中&#xff0c;通过收集、理解、分析和记录用户和系统对系统或产品的需求&#xff0c;以确定其详细的特征和功能。它是一个关键的过程&#xff0c;旨在确保项目成功地满足用户的需求和期望。 在进行需求分析时&#xff0c;有一些…
阅读更多...
推荐文章

Copyright @ 2022~2023