目录
二叉树的定义:
二叉树的应用:
认识二叉树:
二叉树的基本形式:
二叉树的节点:
二叉树的高度和深度:
二叉树的子树:
二叉树的度:
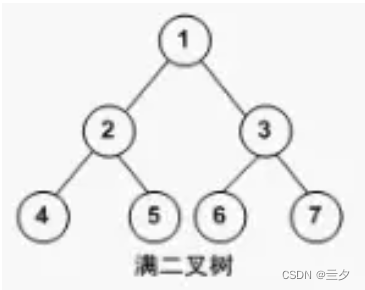
满二叉树:
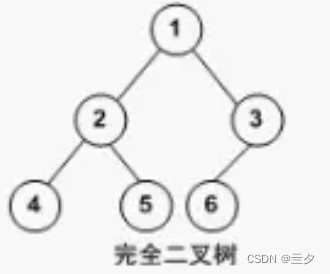
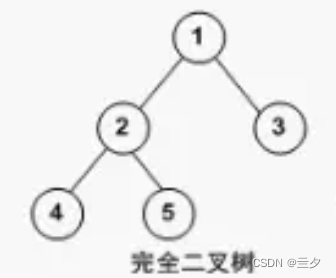
完全二叉树:
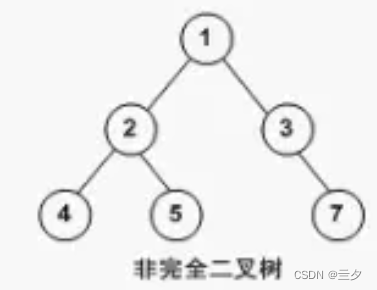
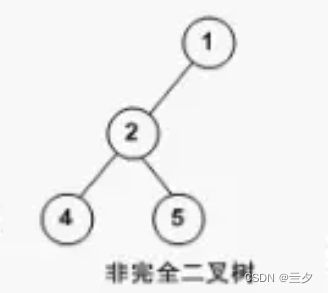
非完全二叉树:
平衡二叉查找数:
二叉树的定义:
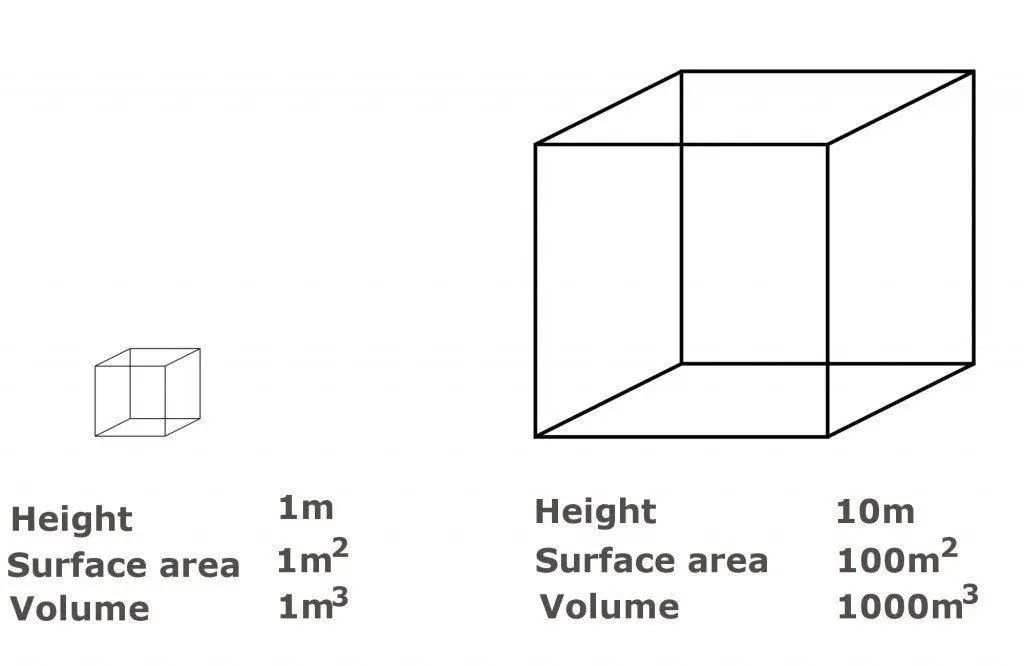
二叉树(Binary tree)是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式,即使是一般的树也能简单地转换为二叉树,而且二叉树的存储结构及其算法都较为简单,因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树,且有左右之分 。
二叉树是n个有限元素的集合,该集合或者为空、或者由一个称为根(root)的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成,是有序树。当集合为空时,称该二叉树为空二叉树。在二叉树中,一个元素也称作一个节点 。
二叉树的应用:
二叉树的部分应用有:1.可以查找自己家族的族谱,至少上溯至祖爷爷辈。2.用于海量数据并发查询。3.在实际使用时会根据链表和有序数组等数据结构的不同优势进行选择。有序数组的优势在于二分查找,链表的优势在于数据项的插入和数据项的删除。但是在有序数组中插入数据就会很慢,而在链表中查找数据项效率较低。而二叉树可以利用链表和有序数组的优势,也可以合并有序数组和链表的优势,二叉树也是一种常用的数据结构。
认识二叉树:
二叉树的基本形式:
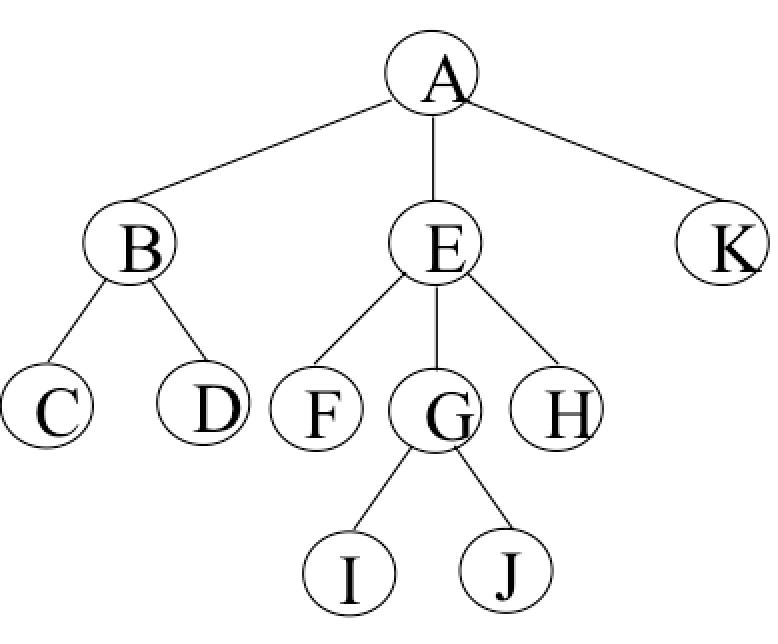
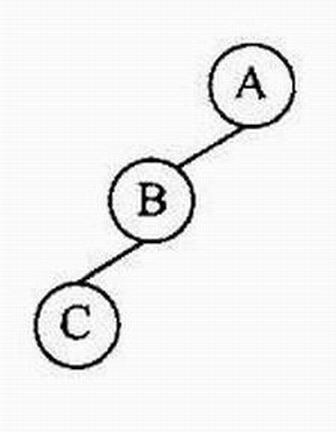
二叉树的基本树形结构如图所示
------------------------------------------------------------------------------
非二叉树
二叉树的节点:
什么是二叉树的节点?
二叉树中每个元素都称为节点。
这里所说元素就是二叉树圆圈里包含的数字或其他元素。
如满二叉树中1~7都是二叉树的节点。
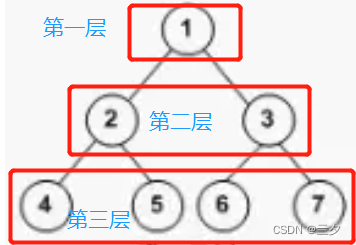
我们将二叉树分层来看
节点的层次定义为:从根节点开始,假设根节点为第1层,根节点的子节点为第2层,依此类推,如果某一个节点位于第L层,则其子节点位于第L+1层 。
那么在第 i 层最多有
个节点
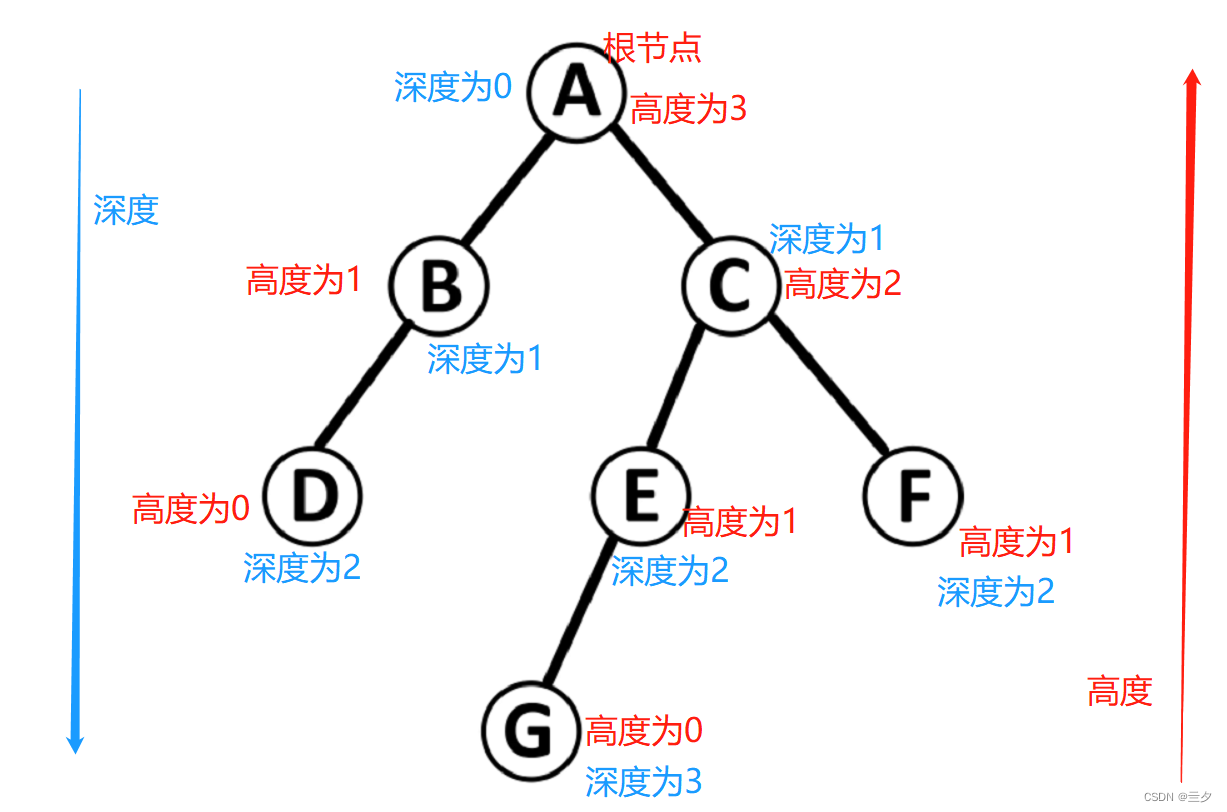
二叉树的高度和深度:
我们先给出二叉树高度和深度的定义
对于某节点来说
- 深度是指从根节点到该节点的最长简单路径边的条数
- 高度是指从最下面的叶子节点到该节点的最长简单路径边的条数
对二叉树
- 深度是从根节点数到它的叶节点
- 高度是从叶节点数到它的根节点
我们来看图
计算某点深度时,我们从根节点出发,向下计算 从根节点到该点的深度。
计算某点的高度时,我们从最底层的叶子节点出发,向上计算到该节点的高度。
值得注意的是,整个二叉树的高度和深度是一样的。如上图二叉树的高度=深度=3,但是节点的高度和深度一般不同。(这时在根节点深度定义为0的情况下,有时一些题目会将根节点深度定义为1,百度百科将根节点定义为0)
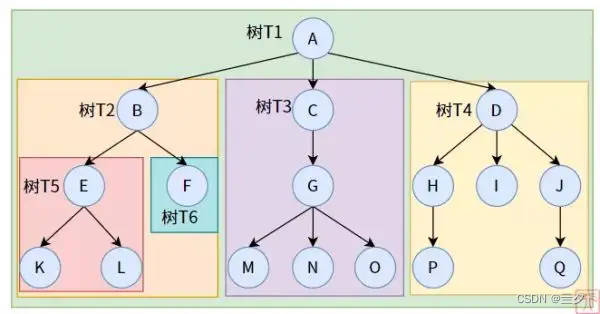
二叉树的子树:
图中的英文字母表示节点的值。图中标出了T1 ~ T6的数(T1~T6仅为部分子树)。子树其实就是整个二叉树的一部分吧分枝,且二叉树的子树需要包含有最底层的节点。比如T2(橙色部分)是一个子树,但是B,E,F却不构成子树。
我们在来看两个特别的子树。其中T1是整个二叉数,T1也可以看成自身的字数。T6也是一个子树,只是这个子树没有分支只有一个节点所以我们习称为节点。
对于度为零的节点也叫做叶子节点
二叉树的度:
二叉树的度表示节点的子树或直接继承者的数目,二叉树的度是一个子树或单子树。
1度就代表只有一个子节点或者它是单子树,2度就代表有两个子节点或是左右子树都有,最大度数为2。并且两个子树有左右之分,顺序不可颠倒。
单子树形如
我们接着来说度
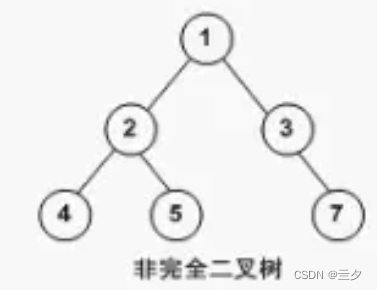
对于度,我们可以理解为某个节点直接含有的分支数。
这个分支数是从有方向的,只能从上层往上层数。
比如(按圆圈中的数字命名节点),
节点1,2含有两个直接的分支,分别为2分支和3分支,所以节点1的度为2。(从2节点到1的是下层到上层的关系,不算一个分支)
节点3只有一个直接的分支,连接到7节点,所以节点3的度为1。
节点4,5,7没有分支,所以节点4,5,7的度为0。
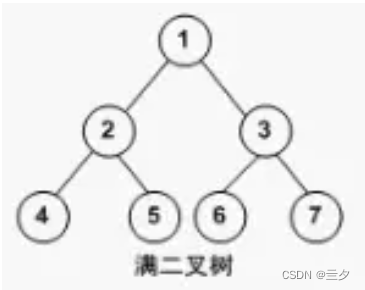
满二叉树:
除最后一层无任何子节点外,每一层上的所有结点都有两个子结点的二叉树。
满二叉树在每个子节点(除最后一层的节点)度都为二的情况下,整个二叉树最多有
个节点。
(一棵满二叉树的每一个结点要么是叶子结点,要么它有两个子结点,但是反过来不成立,因为完全二叉树也满足这个要求,但不是满二叉树)
那么下图的二叉树是满二叉树吗?
满二叉树的结点要么是叶子结点,度为0,要么是度为2的结点,不存在度为1的结点。
因此,图3中这个二叉树也是满二叉树。但是按照国内的定义,它却不是满二叉树。
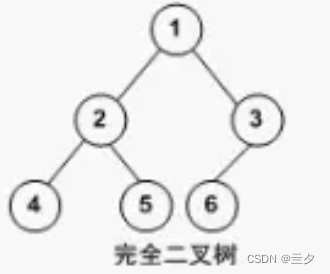
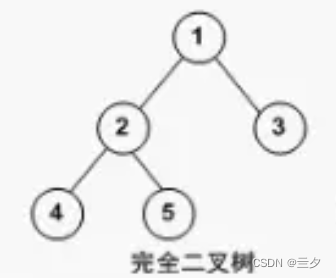
完全二叉树:
除最后⼀层不满外,其余层的都达到该层的最⼤节点数,最后如果不满,该层所有节点都全部靠左排
这里的靠左排是指分支指向靠左
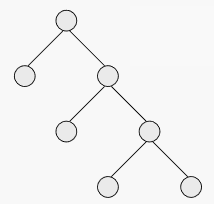
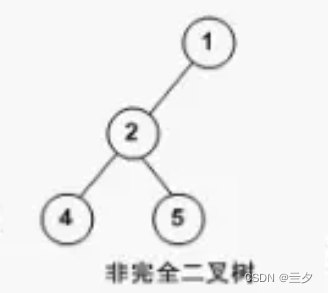
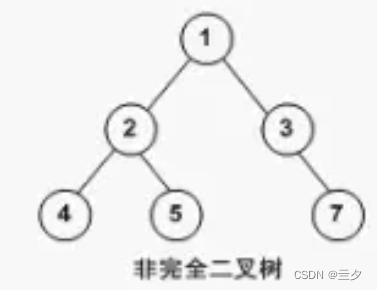
非完全二叉树:
存在不满层数(除最后一层)或者叶子节点靠右排的二叉树
第一层不满
7叶子节点靠右排
平衡二叉查找数:
又称高度平衡树,简称平衡二叉树
定义:
- 可以是空树。
- 假如不是空树,任何一个结点的左子树与右子树都是平衡二叉树,并且高度或深度之差的绝对值不超过 1。
其中左子树高度 - 右子树高度 = 左子树深度 - 右子树深度 = 平衡因子(BF Balance Factor)
对于平衡二叉树我们主要就在于它的平衡,而他的平衡体现以高度差来衡量。
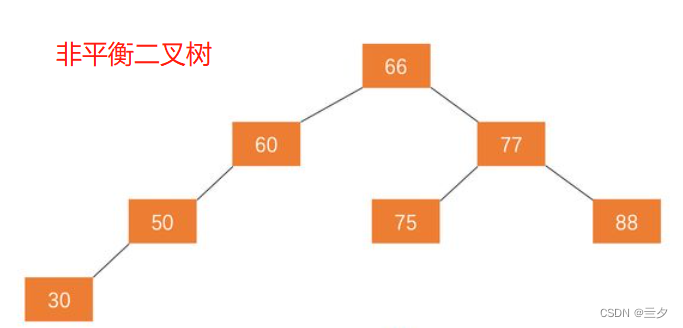
我们再来看非平衡二叉树
对于非平衡二叉树我们可以通过旋转将其转换为平衡二叉树,涉及内容较多,这里先不展开讲。
定义中的子树高度值之差绝对值不超过一怎么理解呢?
上面我们已经分析了二叉树的高度和深度。
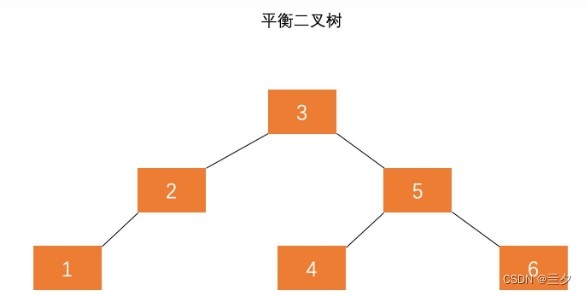
下面我们来计算二叉树各个节点的平衡因子
我们以高度差计算平衡因子 左子树高度 - 右子树高度=平衡因子
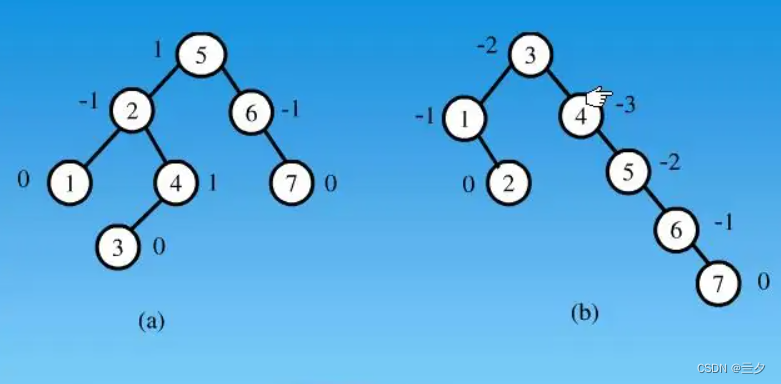
(a)平衡二叉树
5的结点平衡因子就是 3 - 2 = 1;
2的结点平衡因子就是 1 - 2 = -1;
4的结点平衡因子就是 1 - 0 = 1;
6的结点平衡因子就是 0 - 1 = -1;
叶子结点都是为 0;
(b)不平衡二叉树
此节点往下 左子树高度- 右子树高度=平衡因子
3 的结点平衡因子就是 2 - 4 = -2;
1 的结点平衡因子就是 0 - 1 = -1;
4 的结点平衡因子就是 0 - 3 = -3;
5 的结点平衡因子就是 0 - 2 = -2;
6 的结点平衡因子就是 0 - 1 = -1;
叶子结点都是为 0;
平衡二叉树平衡因子绝对值 <= 1
下期将介绍有关节点,度的相关计算和红黑树,B-树,B+树,字典树,后缀树,广义后缀树,堆等类型。
今天就到这,明天见。🚀
❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄end❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄❄










![[产品07]-产品设计定律-菲茨定律/席克定律](https://img-blog.csdnimg.cn/img_convert/bccb7b4523bd0fa2a689ae87e0fca79c.png)