写在前边的话：你的支持是我写作的动力，有帮助到你的话麻烦点赞加收藏呦。感激不尽！如有错误也请留言指正

目录

 

一、完全二叉树 节点总数的特点

二、二叉树 度的特点

     1.n0与n2的关系

     2.节点总数和度的关系

三、例题

     例题一

     例题二

     例题三

---

一、完全二叉树 节点总数的特点

设完全二叉树节点总数为n，那么有如下结论

• n为奇数时，完全二叉树中没有度为1的节点：我们可以这样看，完全二叉树第一层有一个节点，若想完全二叉树的总结点数是奇数，下面的每一行节点数都必须是偶数。所以，每个节点要么度为0，要么度为2。此时  n = n0 + n2

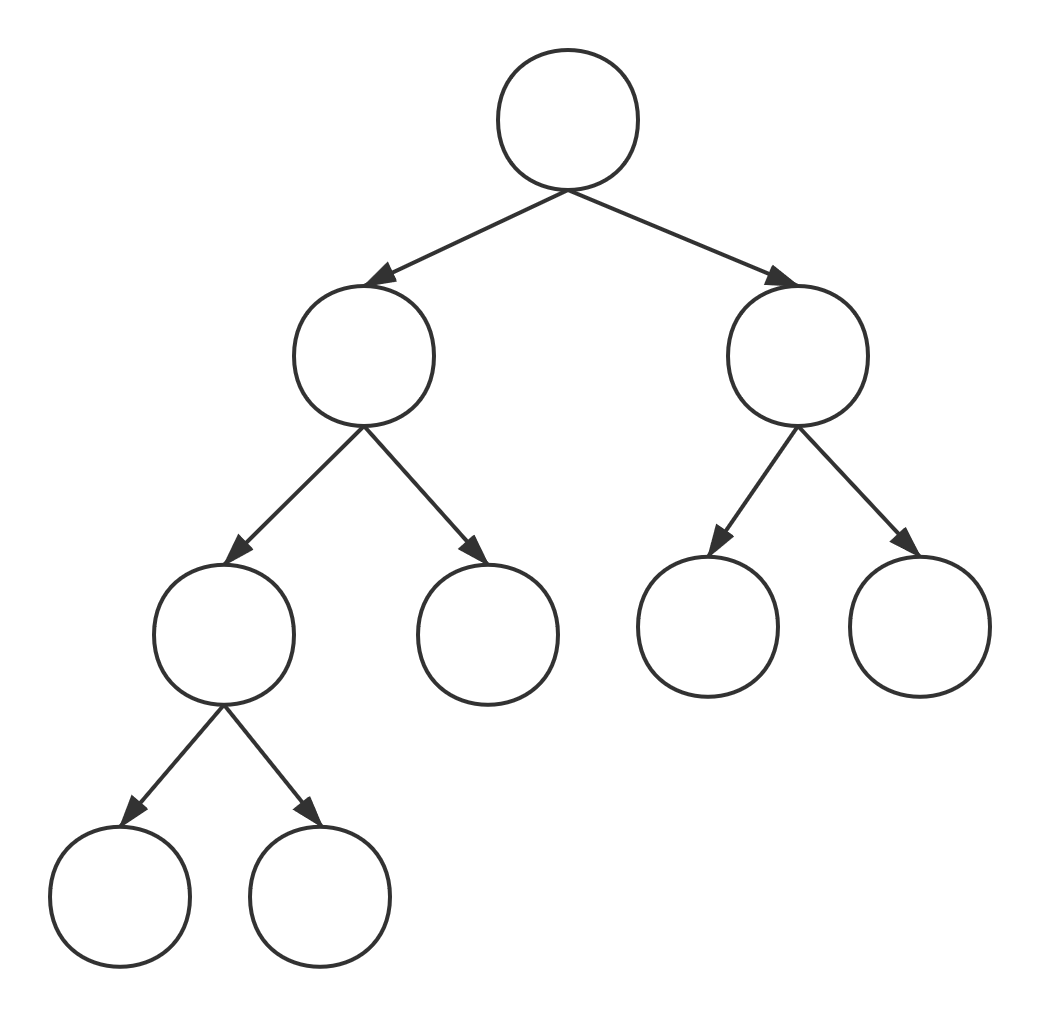
• n为偶数时，完全二叉树中只有一个度为1的节点：完全二叉树第一层有一个节点，若想总节点数为偶数，最后一层必须是奇数个节点。那么单独出来的这个节点的双亲，度就为1。而且也只有它一个度为1的节点。 此时 n = n0 + 1 + n2

 

---

二、二叉树 度的特点

1.n0与n2的关系

• n0 = n2 + 1

2.节点总数和度的关系

• 度=节点总数-1。在树中，每个节点有多少条边出去，该节点的度就为多少。也就是说，一条边贡献一个度。而树中，边的条数是节点数减去1。计算节点数一般的方法是 n=n0+n1+n2+... 所以度和节点的关系就是，度=节点总数-1

---

三、例题

例题一

若一颗完全二叉树有768个节点，则二叉树中叶节点的个数是（）【2011年全国试题4（2分）】

A. 257
B. 258
C. 384
D. 385

 解析：完全二叉树的节点数是偶数，度为1的节点只有一个。n = n0 + 1 + n2；n0 = n2 + 1；解这两个方程组，解得n0 = 384。所以选择C

---

例题二

若一颗完全二叉树上有1001个节点，其中叶节点的个数是（）【西安交通大学 1996 三、2（3分）】
A. 250
B. 500
C. 254
D. 505
E. 以上答案都不对

 解析：完全二叉树节点数是奇数，没有度为1的节点。n = n0 + n2；n0 = n2 + 1；解这两个方程组，解得n0=501。所以选择E

---

例题三

一颗度为4的树T，若有20个度为4的节点，10个度为3的节点，1个度为2的节点，10个度为1的节点，则树T的叶节点个数是（）【2010年全国试题5（2分）】

A. 41
B. 82
C. 113
D. 122

解析：通过度表示的度，和通过节点总数表示的度应该相等

• 度度=20*4+10*3+1*2+10*1
• 点度=20+10+1+10+n0 - 1

n0 = 82，选择B

---

 写在后边的话：你的支持是我写作的动力，有帮助到你的话麻烦点赞加收藏呦。感激不尽！如有错误也请留言指正