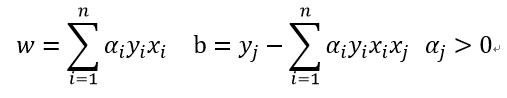SVM现在主流的有两个方法。一个是传统的推导,计算支持向量求解的方法,一个是近几年兴起的梯度下降的方法。 梯度下降方法的核心是使用了hinge loss作为损失函数,所以最近也有人提出的深度SVM其实就是使用hinge loss的神经网络。
本文的目的是讲解传统的推导。
SVM的超平面
SVM模型的基本原理,就是寻找一个合适的超平面,把两类的样本正确分开。单个SVM只能处理二分类,多分类需要多个SVM。
【什么是超平面?】
超平面就是n维度空间的n-1维度的子空间。换成人话就是2维空间中的1维度的线,三维立体空间的二维平面。
图中总共有5个超平面,那么哪一个是最好的呢?我们认为中间的那个是最好的。因为他对两侧的间隔较大。
SVM基本型
超平面我们可以用这个方程来表示:
w T x + b = 0 \bm{w^Tx}+b=0 wTx+b=0
空间中任意一个点x到这个超平面的垂直距离为:
d = ∣ w T x + b ∣ ∣ ∣ w ∣ ∣ d = \frac{|\bm{w^Tx}+b|}{||\bm{w}||} d=∣∣w∣∣∣wTx+b∣
这里不得不提到一下逻辑回归,对于逻辑回归来说:
就是在超平面一侧的样本,逻辑回归给出的预测类别是1,另外一侧就是0.
但是SVM觉得这样有一些过于绝对了,所以:
不仅仅要一个样本在平面的一侧,还要在平面的这一侧足够远的地方,才能算作某一类的样本。
从图中可以看到,两条虚线之外的点,才是SVM能确定是正样本还是负样本的点。
【什么是支持向量?】
图中距离超平面最近的几个训练样本,并且这几个训练样本可以让上式的等号成立。这个点就是支持向量。
【什么是SVM的间隔】
两个不同类别的支持向量到超平面的最小距离之和。其实也就是 2 ∣ ∣ w ∣ ∣ \frac{2}{||w||} ∣∣w∣∣2
到这里,我们可以隐隐约约的发现,寻找最优的超平面其实等价于寻找一个最大的间隔,或者说让间隔最大化。所以可以得到:
max w , b 2 ∣ ∣ w ∣ ∣ \max_{w,b} \frac{2}{||\bm{w}||} maxw,b∣∣w∣∣2
这个的约束条件就是:让SVM给正样本的打分大于1,给负样本的打分小于-1,也就是:
简化一下这个约束条件,可以得到:
y i ( w T x i + b ) > = 1 y_i(\bm{w^Tx_i}+b)>=1 yi(wTxi+b)>=1
一般我们都是求取最小化问题,所以把最大化max问题取倒数,变成最小化问题:
min w , b ∣ ∣ w ∣ ∣ 2 \min_{w,b} \frac{||\bm{w}||}{2} minw,b2∣∣w∣∣
这里为了后续的计算方便,最小化 ∣ ∣ w ∣ ∣ ||w|| ∣∣w∣∣等价于最小化 ∣ ∣ w ∣ ∣ 2 ||w||^2 ∣∣w∣∣2,所以得到:
min w , b ∣ ∣ w ∣ ∣ 2 2 \min_{w,b} \frac{||\bm{w}||^2}{2} minw,b2∣∣w∣∣2
总之SVM的基本型就是:
SVM求解
现在求得了基本型。现在可以来进一步优化这个最小化问题。但是首当其冲的问题便是,如何处理这个约束条件。这里用到的方法是拉格朗日乘子法。将约束条件以 α i \alpha_i αi的权重加入到优化问题中,所以可以得到:
L o s s ( w , b , α ) = 1 2 ∣ ∣ w ∣ ∣ 2 + ∑ i = 1 m α i ( 1 − y i ( w T x i + b ) ) Loss(\bm{w},b,\bm{\alpha})=\frac{1}{2}||w||^2+\sum^m_{i=1}\alpha_i(1-y_i(w^Tx_i+b)) Loss(w,b,α)=21∣∣w∣∣2+∑i=1mαi(1−yi(wTxi+b))
- 这里的loss就是我们要最小化的对象;
- 这里的m就是支持向量的数量。
为了最小化这个问题,对w和b求偏导数,可以得到:
w = ∑ i = 1 m α i y i x i w = \sum^m_{i=1}{\alpha_iy_ix_i} w=∑i=1mαiyixi
0 = ∑ i = 1 m α i y i 0 = \sum^m_{i=1}{\alpha_iy_i} 0=∑i=1mαiyi
然后把这两个公式代入到:
L o s s ( w , b , α ) = 1 2 ∣ ∣ w ∣ ∣ 2 + ∑ i = 1 m α i ( 1 − y i ( w T x i + b ) ) Loss(\bm{w},b,\bm{\alpha})=\frac{1}{2}||w||^2+\sum^m_{i=1}\alpha_i(1-y_i(w^Tx_i+b)) Loss(w,b,α)=21∣∣w∣∣2+∑i=1mαi(1−yi(wTxi+b))
可以消掉w和b,得到:
约束条件为:
从而根据这个计算出 α i \alpha_i αi的取值,然后得到w和b的取值。
【到底如何求解 α \alpha α?】
上面说的最后一部求解alpha,都是理论可以求解,但是实际中如何做到呢?其实这里如何求解 α \alpha α要用到另外一个条件。
就是上述过程要满足一个叫做KKT的条件(KKT具体是什么有点复杂,就不多说了):
- 想要第三个公式成立,要么 α i \alpha_i αi等于0,要么 y i f ( x i ) − 1 = 0 y_if(x_i)-1=0 yif(xi)−1=0.如果alpha=0,那么意味着这个样本不是支持向量,不应该对SVM超平面起到任何影响,所以是不可能的。所以只有 y i f ( x i ) − 1 = 0 y_if(x_i)-1=0 yif(xi)−1=0。
加上了这个条件,我们可以求解出来 α i \alpha_i αi的具体数值,然后求解w和b的数值。
假设有3个支持向量,那么就会有三个 α 1 , α 2 , α 3 \alpha_1, \alpha_2, \alpha_3 α1,α2,α3 ,然后根据 y i f ( x i ) − 1 = 0 y_if(x_i)-1=0 yif(xi)−1=0可以列出3个关于 α 1 , α 2 , α 3 \alpha_1,\alpha_2,\alpha_3 α1,α2,α3的三元一次方程组,然后得到唯一解。