XDOJ（智慧平台）--分配宝藏（用动态规划dp算法解决）(C语言)

------------------------------------------------------------
作为西电渣渣，这是我第一次接触需要一些很明确的算法的题目。

_{第一次博客写废话较多hhh，可以直接到下面看分析}

我在昨天晚上和舍友一起肝这道题，肝了一个晚上都没有解决，甚至没有一个很明确的思路。以至于躺在床上都想着怎么写这道题 ~~（毕竟智慧平台上都会出现的题目，难道期末考试不会考吗）~~ 于是来社区看看有没有西电学长 ~~（其实更希望是学姐）~~ 这里推一推学长的博客 XDU-分配宝藏。

但是本人看着稍微有点复杂的代码就头疼，于是去b站找了dp算法的视频动态规划DP0-1背包，看了一半恍然大悟（假的）写出来一个递归函数交上去，发现一半的例子都超时了（泪目）。看完视频才知道dp算法是怎么样写的。
在这里插入图片描述
然后就这样心血来潮，写下这篇博客。
本文章（大概、或许、可能）算是视频和学长博客的结合吧。
------------------------------------------------------------

内容

一. Dynamic Programming (DP算法)
二. 举例（斐波那契数列，0-1背包）
三. 分配宝藏
------------------------------------------------------------

一、Dynamic Programming (DP算法)

_{DP，听起来挺高级的一个东西，我第一次接触是在洛谷上，但是当时感觉学这玩意还早，就忽视了它，直到我在XDOJ上遇到了它，就有了这篇博客…}
DP，中文名译为动态规划，是求解决策过程最优化的过程。各个阶段采取的决策，一般来说是与时间有关的，决策依赖于当前状态，又随即引起状态的转移，一个决策序列就是在 变化的状态中 产生出来的，故有“动态”的含义。（参考百度百科—动态规划）
下面将直接用例子来说明dp算法。

二、举例（斐波那契数列，0-1背包）

例1. 斐波那契数列

众所周知，斐波那契数列是这样的：
F(0)=1
F(1)=1
F(n)=F(n - 1)+F(n - 2)（n ≥ 2，n ∈ N*）
实际上，这个公式就是一个递归的思路，从我们需要求的那个值逐个归回到F(0)和F(1)
由这个公式我们可以写出一个递归函数，其中递归结束的标志是n=0或n=1.

int F(int n){int res;if(n<2) res=1;else res=F(n-1)+F(n-2);return res;
}
//再简化一下可以写成这样
int F(int n){return n<2?1:F(n-1)+F(n-2);
}

又众所周知,函数调用需要额外的空间（栈）来完成，在调用次数很多的情况下会降低程序效率，并且递归调用可能会导致大量的重复计算。所以我们需要把这个递归函数改造成一个效率更高的形式。
可以看到，递归是从我们要的F(n)一直计算到F(0)和F(1)，然后再返回到F(n)。在这个过程中，程序在不断地分配空间，降低效率，那我们该怎么改才能提高效率呢？

举个栗子，在Minecraft中，有一处悬崖，附近有一扇门，而门的钥匙落在了悬崖底部，Steve需要取钥匙开门。他有两种方法，一个是递归，一个是dp。

递归意味着他从悬崖下去，但他不知道悬崖的高度，因此需要不断地造梯子，爬下来，再返回，来完成这个任务。

而dp，真是个好东西。它将Steve传送到了悬崖的底部，并且告诉他悬崖的高度。这个时候，Steve只需要造一定数量的梯子直接搭上去完成任务。~~（咳咳，这个例子可能有点离谱，但是无伤大雅，dddd）~~

按照这个想法，递归就相当于从高层走向底层，再返回高层；dp就是从底层打基础到高层，效率更高。
那如何打基础呢？（再回到斐波那契数列）
我们知道当n>2的时候，F(n)=F(n-1)+F(n-2)，一直到F(0)和F(1)，而F(0)和F(1)就是最基础的基础。（这个时候有小伙伴就要说了，递归函数不也有这个基础吗？答：不要在意这些细节~）dp就是要从基础入手，又又众所周知，要求F(n)，就要把F(n-1)到F(0)全部求一遍，那就求呀。由此我们可以写出这么一段代码：

int F[10000];					//数组多大无所谓，只要够用就行
F[0]=F[1]=1;					//初始化F[0]和F[1]
for(int i=2;i<=n;i++)        	//从F[2]开始到F[n]F[i]=F[i-1]+F[i-2];			//套公式//改写成函数
int Fib(int n){int F[10000]={1,1};for(int i=2;i<=n;i++)F[i]=F[i-1]+F[i-2];return F[n];
}

然后，dp这个方法就写完了，然后可能有的小伙伴就懵了，直呼就这？
没错，就这，我们要的F[n]就出来了。
_{（这时候我突然想起，在刚学递归的时候，其实就接触到了这样简单的dp）}
实际上dp算法就像学长@西电蔡徐坤所说的记忆化搜索一样，取之前已经计算过的值，效率更高。
_{这时候就有小伙伴说了，那递归岂不是一无是处，当然不是了，在很多算法中，有递归做得到而dp做不到的地方，以后或许能够接触到}

例2. 0-1背包问题

做完一维的，这个时候再来个二维岂不妙哉~
在这里插入图片描述
如图所示，这就是一个经典的0-1背包问题。
我们设V为背包价值，k为能偷的物品数量，w为背包容量，w_i 为第 i 件物品的重量，v_i 为第i件物品的价值，则有V=V( k , w )。
在这题中，我们要求的就是V( 4 , 8 )。我们选择从第k件（也就是第四件）开始偷，然后是k-1，k-2 … 2，1件。

从第4件物品开始，我们可以选择偷和不偷。
①.如果选择偷，那么V( 4 , 8 )=V( 4 - 1 , 8 - w₄ ) + v₄=V( 3 , 3 ) + 8
②.如果选择不偷，则V( 4 , 8 )=V( 4 - 1 , 8 )=V( 3 , 8 )
取①的结果V( 3 , 3 ) + 8
③.发现这个时候的 w（背包容量）< w₃，因此只能选择不偷，所以V( 3 , 3 ) + 8=V( 2 , 3 ) + 8
取②的结果V( 3 , 8 )
④.选择偷，那么V( 3 , 8 )=V( 3 - 1 , 8 - w₃ ) + v₃=V( 2 , 4 ) + 5
⑤.选择不偷，则V( 3 , 8 )=V( 3 - 1 , 8 )=V( 2 , 8 )
••••••
这样推下去，我们可以得到这样的一个简单公式
在这里插入图片描述
而我们要求的应该是最大值，再加上背包容量不够的情况，得到状态转移方程

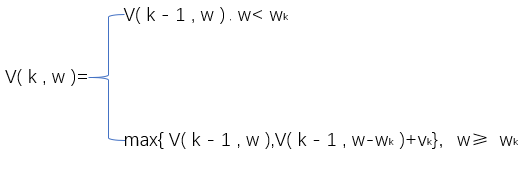
在这里插入图片描述
看到这里各位小伙伴是不是就可以写一个递归函数出来了，这里我就不再写了（懒）。
那这个递归结束的标志应该是什么呢？
不难想到，当能偷的物品数量为0或者背包剩余容量为0时，递归就该结束了。
因此V( k , 0 )=V( 0 , w )≡0
可以得到这么一个表格
在这里插入图片描述
由此按照例1的思想，是不是就直接能写出代码呢？
这里给出代码片段，剩下的交给小伙伴们自己写出来。

int v[5][9]={0};					
int w[]={0,2,3,4,5};
int v[]={0,3,4,5,8};
for(int k = 1; k <= 4; k++)						//k表示第k件物品for(int W = 1;W <= 8; W++){					//W表示背包剩余容量为Wif(w[i]>W)								//物品重量大于背包剩余容量，不偷v[k][W]=v[k-1][W];else									//否则,从偷和不偷中选出最大值v[k][W]=max( v[k-1][W] ,v[k-1][W-w[k]]+v[k] );//max函数自己写,或者用a?b:c表达式}											//v[4][8]就是要的答案

三、分配宝藏

~~事件的导火索可不能忘了~~

标题
分配宝藏
类别
综合
时间限制
2s
内存限制
256Kb
问题描述
两个寻宝者找到一个宝藏，里面包含n件物品，每件物品的价值分别是W[0]，W[1]，…W[n-1]。
SumA代表寻宝者A所获物品价值总和，SumB代表寻宝者B所获物品价值总和，请问怎么分配才能使得两人所获物品价值总和差距最小，即两人所获物品价值总和之差的绝对值|SumA - SumB|最小。
输入说明
输入数据由两行构成：
第一行为一个正整数n，表示物品个数，其中0<n<=200。
第二行有n个正整数，分别代表每件物品的价值W[i]，其中0<W[i]<=200。

输出说明
对于每组数据，输出一个整数|SumA-SumB|，表示两人所获物品价值总和之差的最小值。

输入样例
4
1 2 3 4

输出样例
0

题目分析
这道题和例题2很像，但唯一不同的就是，物品的重量相当于价值。
题目要求A与B之差的绝对值最小，而物品总价值时固定的，因此将背包容量设为sum/2。

下面直接给出我的代码（尽量用代码里的注释解释代码）

#include<stdio.h>
int W[201], sum, dp[201][20001];	//[201]是便于将物品从1开始编号//[20001]同理
int max(int a,int b);
int main(void)
{int n, i, j, sumA;				//假设A得到的永远是较少的那个scanf( "%d", &n);for(i = 1; i <= n; i++){	i代指第i个物品scanf( "%d", &W[i] );sum += W[i];}for(i = 1; i <= n; i++){if (W[i] > sum/2){			//如果物品某个价值大于总价值的一半,其余物品将给A，不需要再计算dp[n][sum/2] =sum-W[i];break;}for(j = 1; j <= sum/2; j++){//j分别代指第i个物品和背包剩余容量if(W[i] > j) 			//同样的，物品重量大于背包剩余容量，不偷dp[i][j] = dp[i-1][j];else dp[i][j] = max( dp[i-1][j] , dp[i-1][j-W[i]] + W[i]);}}sumA = dp[n][sum/2];//个人比较喜欢单一出口printf("%d\n", sum - 2 * sumA);//因为A总是得到较少的那个，不需要再加上绝对值return 0;
}
int max(int a,int b){int m = a;if( a < b) m = b;return m;
}