1、SVM思想

（1）SVM算法的依据就是分类器B的分类间隔比分类器C的分类间隔大。这里涉及到第一个SVM独有的概念”分类间隔”。在保证决策面方向不变且不会出现错分样本的情况下移动决策面，会在原来的决策面两侧找到两个极限位置（越过该位置就会产生错分现象），如虚线所示。虚线的位置由决策面的方向和距离原决策面最近的几个样本的位置决定。而这两条平行虚线正中间的分界线就是在保持当前决策面方向不变的前提下的最优决策面。两条虚线之间的垂直距离就是这个最优决策面对应的分类间隔。显然每一个可能把数据集正确分开的方向都有一个最优决策面（有些方向无论如何移动决策面的位置也不可能将两类样本完全分开），而不同方向的最优决策面的分类间隔通常是不同的，那个具有“最大间隔”的决策面就是SVM要寻找的最优解。而这个真正的最优解对应的两侧虚线所穿过的样本点，就是SVM中的支持样本点，称为”支持向量”。

（2）理解：二维平面，两类不同的数据能找到一直线将其分割开，但此直线是可以有很多个方向的，SVM的核心思想就是先找两条极限位置的线（如图虚线），将两类数据划个边界（越过该位置就会产生错分现象），然后找出能使这两条虚线的间隔最大的方向，其中心平行线即为超平面，超平面经过的样本点即为支持向量

2、公式推导

（1）点到线的距离：

直线方程为Ax0+By0+C=0，点P的坐标为(x0,y0)

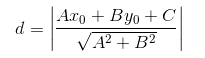
（2）决策方程：（超平面）

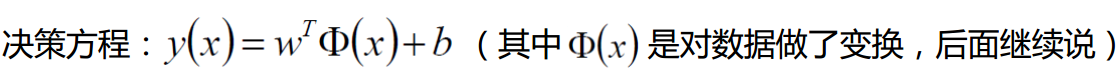
数据集：(X1,Y1)(X2,Y2)… (Xn,Yn)
Y为样本的类别： 当X为正例时候 Y = +1 当X为负例时候 Y = -1
（因为距离公式的分子是正的，所以乘上y_i，不论y_i取正一还是负一，y_i相乘y(xi)后都得到大于0的数）

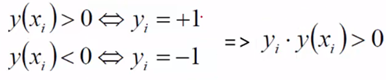
得到转换的距离公式：（乘y_i即可去掉绝对值符号）

（3）目标函数：

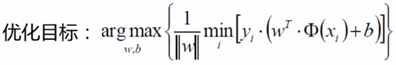
• A：
  i min：每个样本点都与超平面有一个距离，先通过min找出与超平面距离最小的点，即“支持向量”
  ii max:找出距离最小的点之后，再通过max求得使超平面与支持向量点间距最大的距离的w、b参数
  
• B ：
  放缩变换（化简）：（原式子由恒大于0变为恒大于1，变得更加严格，即切分的点要在超平面的正负1范围之外）
  
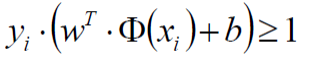
• C ：
  最终化简式子：（有放缩变化得所求min的最小值为1），由此可得min的结果等于1；

（4）目标函数的求解：

所以当前目标变成了：

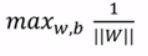
约束条件为：

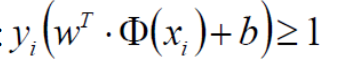
要求解最大值，将问题转换为最小值的问题：

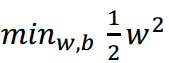
使用拉格朗日乘子法可以得到其“对偶问题”。
这是拉格朗日对偶性，即，通过给每一个约束条件加上一个拉格朗日乘子。然后定义出拉格朗日函数，通过拉格朗日函数将约束条件融合进目标函数中。目的是，只需要通过一个目标函数包含约束条件，便可以清楚解释问题。
通过拉格朗日乘子法求解min：（不等式约束）
拉格朗日乘子法简单说就是：约束条件为g(x,y) 求f(x,y)的极值，需找到两函数相切的点，即为极值点（若不相切，则表示沿着g(x,y)切线的方向，还能使f(x,y)增长，所以还不是极值点）
其有三种类型：

• 1、一个等式约束
• 2、多个等式约束
• 3、既有等式约束又有不等式约束
  
  而这里的求解min，只有一个等式约束：
  
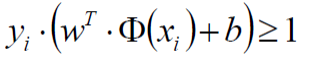
  所以通过转换我们的目标函数得到：
  
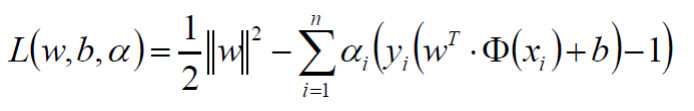
  为什么使用这样的拉格朗日乘子，又为何这样构建？这实际上是因为我们的目标函数是不等式约束，解这样的二次规划问题，我们选择用KKT条件，而KKT条件需要这样的一个约束 ai>0（拉格朗日乘子ai） 。最终我们便通过KKT条件来产生原问题的对偶问题，从而高效的求出结果。
  
  应用KKT条件：（先完成第一步min的求解得出w、b）
  
  （第二步求最大值）
  
  求解例子：
  
  
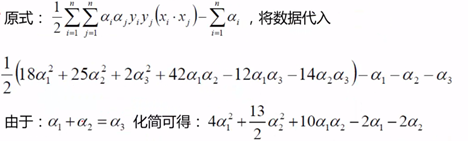
  偏导：
  
  
  
  
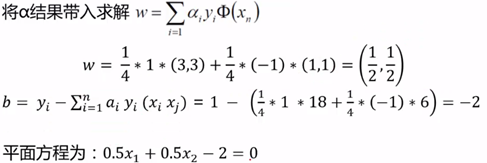
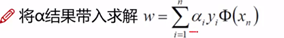
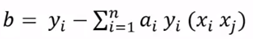
  （w=a*y,当a等于0时，对超平面的方程是没有影响的，所以支持向量为a!=0的点）
  得到超平面方程

3、软间隔：

C通过交叉验证集选择合适的数

加入松弛因子，超平面不用分的很绝对

参数C决定松弛程度：

带参数松弛因子的求解：

手推公式：

min max和max min是有弱对偶关系的，但是原问题又是凸二次规划问题（二次规划：原问题是二次的，约束是线性的），所以min max和max min升级为强对偶关系
而原问题和对偶问题具有强对偶关系的充要条件就是KKT条件。

拉格朗日转换恒等的逻辑证明：