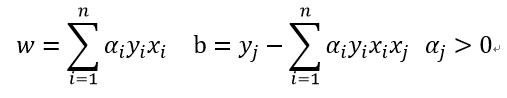这两天要用到SVR的几何解释,特地又翻了CS229 lecture3的笔记。特此记录一下我理解的思路。
- 从logistic regression引入,说明我们应该更关注于离separating hyperplane近的点,进而引入了margin的概念。
- 我们想让margin尽量的大,但最直接的functional margin可以通过缩放ω和b来任意控制。这里我们当然可以固定ω 2-norm=1,但暂时先不这样做。
- 为此,我们引入了geometric margin。functional magrin就是直接的 ωT*x+b,geometric margin就不那么直接,大概有以下几点:
- 向量OA-向量BA=向量OB
- 向量OA=point A,向量BA=geometric_margin*ω的法向量。而ω的法向量=ω/ω 2-norm
- 1,2得到point B,又因为B在separating hyperplane上,所以 将point B带入ωT*x+b=0
- 将3带入的式子略加转换,就得到一个关于geometric margin的等式。
- 进一步还以发现,geometric margin = functional margin/ ω 2-norm

- 下一步就是maximize minimum geometric margin,但由于约束条件2是非凸的。所以,将优化目标由maximize minimum geometric margin改变为maximize minimum functional margin/ω 2-norm。这里需要注意一点,第一个约束项的右式从geometric margin变成了functional margin,其原因在于约束项本来就该是functional margin,只是当ω 2-norm是1的时候,functional margin与geometric margin相等且优化目标是geometric margin,才在约束项中使用的geometric margin。所以当ω 2-norm不为1时