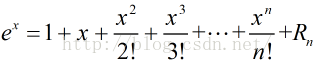目录

一、硬间隔SVM（Hard Margin SVM)

二、对偶问题（Dual Problem)

 1.将有约束问题转变为无约束问题

 2.强对偶关系

3.计算拉格朗日函数的最小值

 4.得到对偶形式

三、对偶形式的求解

1.KKT条件的引入

2.计算w*和b*

 四、软间隔SVM（Soft Margin SVM)

1.Hinge Loss的引入

 2.软间隔SVM的形式

---

SVM是一种无监督机器学习方法，常用于二分类问题。其相较于逻辑回归，引入了核函数的概念，对非线性关系有更好的分类效果；同时由于对偶问题的引入，使得计算的复杂性由维度的大小转变为样本的数量，避免了维度爆炸。但是由于SVM的本质是二次规划问题，样本数量大的时候，需要占用大量的存储空间和时间，不容易实现；同时SVM解决多分类问题存在一定困难。

一、硬间隔SVM（Hard Margin SVM)

硬间隔SVM是一个二次凸规划问题，其形式为：

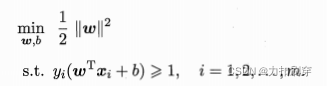
其推导过程为：

（1）列出原始目标函数和约束条件。

目标函数：使间隔最大（间隔指离分隔线最近点到分隔线的距离）

约束条件：分隔线两侧的所有点均属于同一类别

即：

其中，间隔（最小距离）的推导过程如下：

 （2）表达式化简

目标函数中，由于w与x无关，所以可以将1/||w||提出来；

由第一步得到的约束条件可知，必定存在一个γ>0，使得所有样本到分隔线的距离>γ，即：

 这样，可以将目标函数中的min后所有元素进行替换，即：

 （3）最终形式

目标函数：将max化为min，转化为二次型

约束条件：由于最小距离等于1，所以所有样本的距离大于等于1

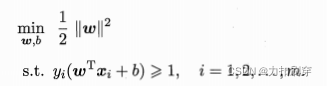
二、对偶问题（Dual Problem)

在本问题中，可以将上面推出的二次规划问题转化为对偶形式：

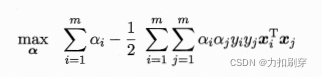
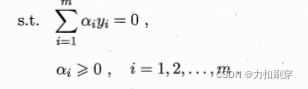
 引入对偶形式后，其目的为：

（1）方便引入核函数

（2）使约束函数从由维度、样本数量有关，变为仅与样本数量有关，方便计算。

其推导过程使用了拉格朗日(Lagrange）乘子法，拉格朗日乘子法方法的推导可参考下面博客。我们在这里仅套用Lagrange乘子法。

深入理解拉格朗日乘子法（Lagrange Multiplier) 和KKT条件_lijil168的博客-CSDN博客_拉格朗日乘子法

 1.将有约束问题转变为无约束问题

带入Lagrange函数以及KKT条件，得到如下形式：

 2.强对偶关系

拉格朗日为凹函数，其仅有最小值，没有最大值。

而目前的形式需要求拉格朗日函数的最大值，无法求得。所以需要对问题进行转变。
拉格朗日函数满足强对偶关系，即min max f(x) = max min f(x），可将上式化简为：

3.计算拉格朗日函数的最小值

拉格朗日函数有唯一最小值，故极小值即为最小值。

极小值的计算方式为：令偏导数等于0

 4.得到对偶形式

代回原目标函数，即可得到最终结果。

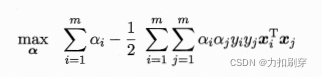
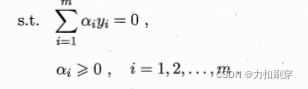
三、对偶形式的求解

1.KKT条件的引入

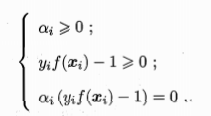
 由KKT条件的第三个式子可知，只有处于支持向量上的点（yf(x)-1=0)才可以满足第三个条件。所以在SVM中，仅有在支持向量上的点才有意义

2.计算w*和b*

w*和b*即为确定超平面的参数。

w*的求解：直接带入条件即可

b*的求解：由于仅有支持向量上的点起作用，所以代回支持向量上的样本点，对b*进行求解。

 四、软间隔SVM（Soft Margin SVM)

引入软间隔SVM的目的是：防止由于噪声数据而产生的过拟合现象。

1.Hinge Loss的引入

Hinge Loss设置了一个阈值，使得偏差数值尽可能小。其函数图像如下。

 2.软间隔SVM的形式