这学期会时不时更新一下伊曼纽尔·德曼(Emanuel Derman) 教授与迈克尔B.米勒(Michael B. Miller)的《The Volatility Smile》这本书,本意是协助导师课程需要,发在这里有意的朋友们可以学习一下,思路不一定够清晰且由于分工原因我是从书本第13章写起,还请大家见谅。
第19章 随机波动率模型入门
随机波动率介绍
本章将研究随机波动率模型,分析波动率独立于股票价格变动的情况
随机波动率建模方法
随机波动率建模最直接的方法就是令股票的波动率取决于某随机因子,而跟股票价格变动无关。通常有如下两种方法:
- 布莱克-斯科尔斯-默顿扩展式。这种方法是从布莱克-斯科尔斯-默顿(BSM)模型出发,该模型中的标的资产服从几何布朗运动,且模型中的隐含波动率不存在斜度。然后令股票的波动率本身成为一个独立的随机变量。我们将发现,这样处理以后,第2个随机变量,也就是波动率的波动率,才是导致微笑曲线的原因。Hull-White随机波动率模型就是这样的一个例子
- 局部波动率扩展式。这种方法是从局部波动率模型出发,这类模型已经可以解释微笑曲线的存在。然后引入一个新的随机因子,令局部波动率本身变成一个随机变量,该随机因子就是导致波动率微笑曲线产生的原因。SABR(stochastic alpha,beta,rho) 模型就是这样的一个例子
在BSM模型中引入随机波动率的启发式方法
假设无风险利率和股息率保持不变,但是股票价格 S S S 和股票波动 σ \sigma σ 均服从随机流程。用 C ( S , t , K , T , σ ) C(S,t,K,T,\sigma) C(S,t,K,T,σ) 表示看涨期权的价格。根据伊藤引理,如果 S , σ S,\sigma S,σ 均是随机变量,那么我们就可以得到期权价格 C C C 变动值的近似表达式:
d C = ∂ C ∂ t d t + ∂ C ∂ S d S + ∂ C ∂ σ d σ + 1 2 ∂ 2 C ∂ S 2 d S 2 + 1 2 ∂ 2 C ∂ σ 2 d σ 2 + ∂ 2 C ∂ S ∂ σ d S d σ = ∂ C ∂ t d t + ∂ C ∂ S d S + ∂ C ∂ σ d σ + 1 2 ∂ 2 C ∂ S 2 σ 2 S 2 d t + 1 2 ∂ 2 C ∂ σ 2 d σ 2 + ∂ 2 C ∂ S ∂ σ d S d σ = ( ∂ C ∂ t + 1 2 ∂ 2 C ∂ S 2 σ 2 S 2 ) d t + ∂ C ∂ S d S + ∂ C ∂ σ d σ + 1 2 ∂ 2 C ∂ σ 2 d σ 2 + ∂ 2 C ∂ S ∂ σ d S d σ dC=\frac{\partial C}{\partial t}dt+\frac{\partial C}{\partial S}dS+\frac{\partial C}{\partial\sigma}d\sigma+\frac{1}{2}\frac{\partial^2C}{\partial S^2}dS^2+\frac{1}{2}\frac{\partial^2C}{\partial\sigma^2}d\sigma^2+\frac{\partial^2C}{\partial S\partial\sigma}dSd\sigma\\=\frac{\partial C}{\partial t}dt+\frac{\partial C}{\partial S}dS+\frac{\partial C}{\partial\sigma}d\sigma+\frac{1}{2}\frac{\partial^2C}{\partial S^2}\sigma^2S^2dt+\frac{1}{2}\frac{\partial^2C}{\partial\sigma^2}d\sigma^2+\frac{\partial^2C}{\partial S\partial\sigma}dSd\sigma\\=(\frac{\partial C}{\partial t}+\frac{1}{2}\frac{\partial^2C}{\partial S^2}\sigma^2S^2)dt+\frac{\partial C}{\partial S}dS+\frac{\partial C}{\partial\sigma}d\sigma+\frac{1}{2}\frac{\partial^2C}{\partial\sigma^2}d\sigma^2+\frac{\partial^2C}{\partial S\partial\sigma}dSd\sigma dC=∂t∂Cdt+∂S∂CdS+∂σ∂Cdσ+21∂S2∂2CdS2+21∂σ2∂2Cdσ2+∂S∂σ∂2CdSdσ=∂t∂Cdt+∂S∂CdS+∂σ∂Cdσ+21∂S2∂2Cσ2S2dt+21∂σ2∂2Cdσ2+∂S∂σ∂2CdSdσ=(∂t∂C+21∂S2∂2Cσ2S2)dt+∂S∂CdS+∂σ∂Cdσ+21∂σ2∂2Cdσ2+∂S∂σ∂2CdSdσ
现在我们将建立一个无风险的对冲策略,买入看涨期权,并卖出恰好足够数量的股票 S S S 和足够的波动率 σ \sigma σ,使得这个对冲组合在某瞬间是无风险的。于是上式中的与 d S dS dS 和 d σ d\sigma dσ 成线性关系的各项均会被消掉,对对冲组合的损益(P&L)的影响为0,组合的损益就变成了:
d C = ( ∂ C ∂ t + 1 2 ∂ 2 C ∂ S 2 σ 2 S 2 ) d t + 1 2 ∂ 2 C ∂ σ 2 d σ 2 + ∂ 2 C ∂ S ∂ σ d S d σ dC=(\frac{\partial C}{\partial t}+\frac{1}{2}\frac{\partial^2C}{\partial S^2}\sigma^2S^2)dt+\frac{1}{2}\frac{\partial^2C}{\partial\sigma^2}d\sigma^2+\frac{\partial^2C}{\partial S\partial\sigma}dSd\sigma dC=(∂t∂C+21∂S2∂2Cσ2S2)dt+21∂σ2∂2Cdσ2+∂S∂σ∂2CdSdσ
为方便继续推导,将上式中的未知偏微分导数替换为 BSM 模型中的偏微分值,并假设无风险利率和股息率都等于0,这种情况下根据BSM方程式,上式中右侧第一个括号里面的各项就可以消掉:
∂ C B S M ∂ t + 1 2 ∂ 2 C B S M ∂ S 2 σ 2 S 2 = 0 \frac{\partial C_{BSM}}{\partial t}+\frac{1}{2}\frac{\partial^2C_{BSM}}{\partial S^2}\sigma^2S^2=0 ∂t∂CBSM+21∂S2∂2CBSMσ2S2=0
于是随机波动率对于对冲组合损益值变动的影响,就可以用如下等式近似表达:
d C = 1 2 ∂ 2 C B S M ∂ σ 2 E [ d σ 2 ] + ∂ 2 C B S M ∂ S ∂ σ E [ d S d σ ] dC=\frac{1}{2}\frac{\partial^2C_{BSM}}{\partial\sigma^2}E[d\sigma^2]+\frac{\partial^2C_{BSM}}{\partial S\partial\sigma}E[dSd\sigma] dC=21∂σ2∂2CBSME[dσ2]+∂S∂σ∂2CBSME[dSdσ]
其中 ∂ 2 C ∂ σ 2 \dfrac{\partial^2C}{\partial\sigma^2} ∂σ2∂2C 通常也被称为volga值,这是用波动率变量的函数来描述看涨期权的凸性。 ∂ 2 C ∂ S ∂ σ \dfrac{\partial^2C}{\partial S\partial\sigma} ∂S∂σ∂2C 通常被称为vanna值、DdeltaDsigma 值或者 DvegaDspot 值。当无风险利率和股息率都等于0的时候,BSM模型下的volga值和vanna值分别等于:
∂ 2 C B S M ∂ σ 2 = V σ [ ln 2 ( S K ) σ 2 τ − σ 2 τ 4 ] ∂ 2 C B S M ∂ S ∂ σ = V S ( 1 2 − 1 σ 2 τ ln ( S K ) ) \frac{\partial^2C_{BSM}}{\partial\sigma^2}=\frac{V}{\sigma}[\frac{\ln^2(\dfrac{S}{K})}{\sigma^2\tau}-\frac{\sigma^2\tau}{4}]\\ \frac{\partial^2C_{BSM}}{\partial S\partial\sigma}=\frac{V}{S}(\frac{1}{2}-\frac{1}{\sigma^2\tau}\ln(\frac{S}{K})) ∂σ2∂2CBSM=σV[σ2τln2(KS)−4σ2τ]∂S∂σ∂2CBSM=SV(21−σ2τ1ln(KS))
其中:
V = ∂ C B S M ∂ σ = τ 2 π S e − 1 2 × ( ln ( S K ) σ τ + σ τ 2 ) 2 V=\frac{\partial C_{BSM}}{\partial\sigma}=\frac{\sqrt{\tau}}{\sqrt{2\pi}}Se^{-\frac{1}{2}\times(\frac{\ln(\frac{S}{K})}{\sigma\sqrt{\tau}}+\frac{\sigma\sqrt{\tau}}{2})^2} V=∂σ∂CBSM=2πτSe−21×(στln(KS)+2στ)2
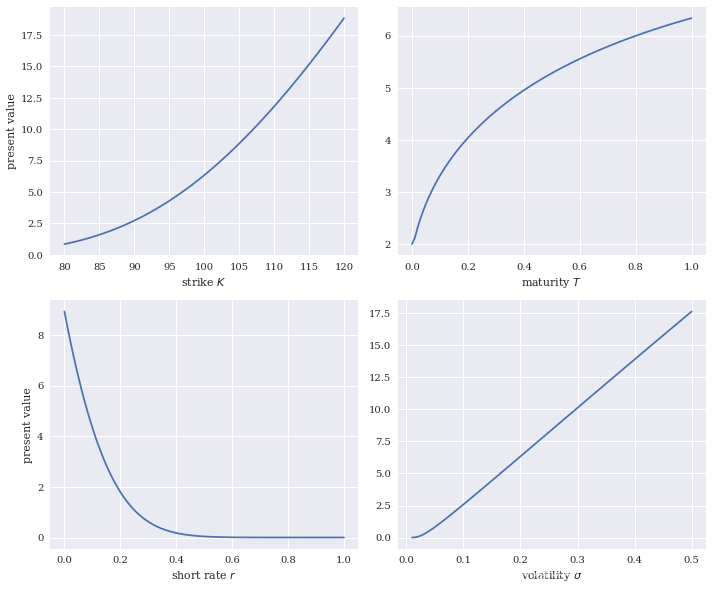
在平值期权附近, ln ( S / K ) \ln(S/K) ln(S/K) 接近于0,除此之外,对于典型的 σ , τ \sigma,\tau σ,τ,BSM的volga值都是正数。下图展示了一个典型的看涨期权BSM volga值情况。由于 E [ d σ 2 ] E[d\sigma^2] E[dσ2] 值总是正数,因此,只要 volga 值为正数,随机波动率总是会增加看涨期权的价值,并使其高于在BSM模型中的价值。对于看跌期权来说,也是如此。总结而言,如果波动率服从随机流程,针对标准期权的对冲组合,需要买入波动率的波动率,买入的大小与波动率的凸性有关,也就是volga值
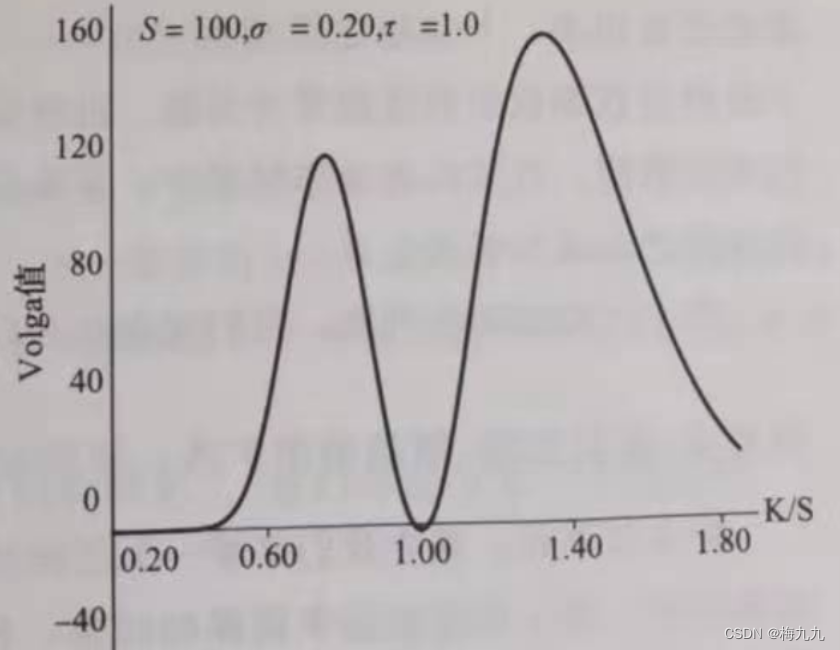
volga 值在平值期权行权价前后分别达到峰值和谷值,如果波动率是随机变量,在期权处于实值状态和虚值状态时的差异是最大的。这就意味着如果波动率服从随机流程,那么当期权的行权价偏离平值行权价的时候,波动率的凸性会使期权的价值增加。这会使虚值期权的价值高于平值期权,进而导致微笑曲线呈现U形,如下图所示
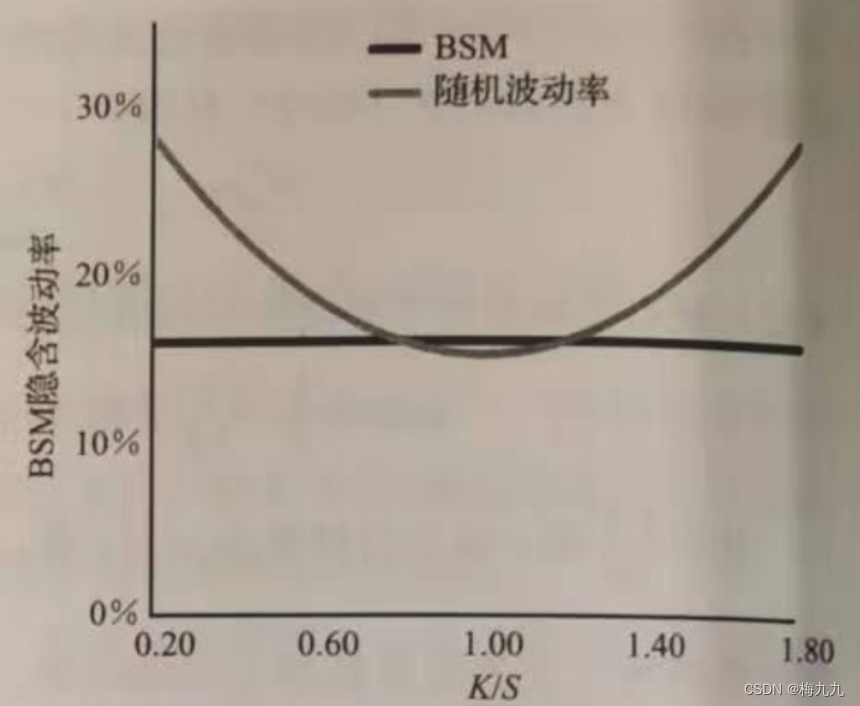
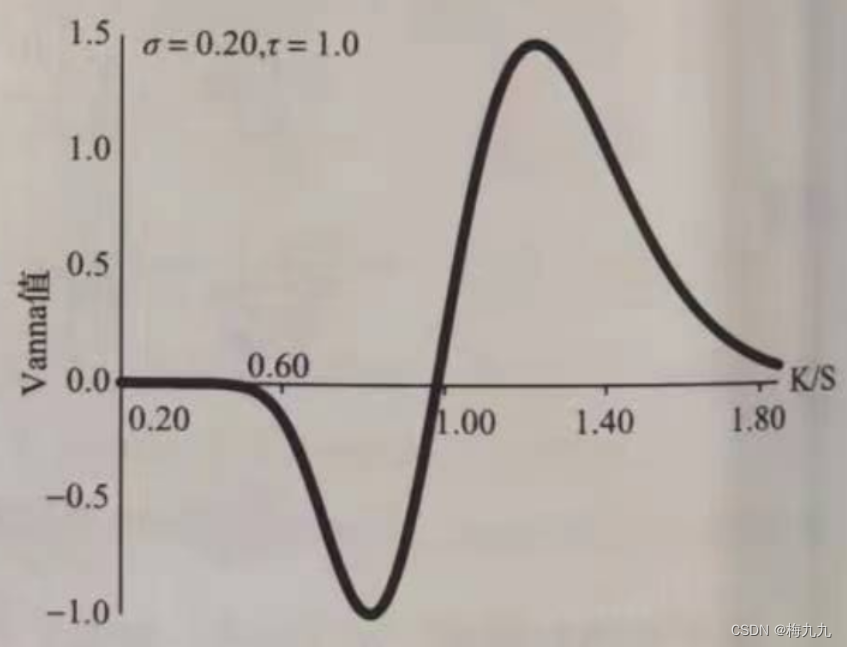
下图展示了以 K / S K/S K/S 为单位的看涨期权BSM vanna值曲线。对于典型的 σ , τ \sigma,\tau σ,τ,当看涨期权处于虚值时( K > S K>S K>S),vanna为正数,而实值时为负数。如果 E [ d S d σ ] E[dSd\sigma] E[dSdσ] 是正数,相对看涨期权的BSM价值,在行权价较高的时候,vanna会增加其价值,反之减少。如果股票价格和波动率负相关,上述结论则相反
布莱克-斯科尔斯-默顿模型扩展:波动率的随机微分方程式
跟股票价格变动建模相似,通常在对波动率建模的时候,我们也假设波动率服从几何布朗运动。Hull-White随机波动率模型是最简单也是最早的该类模型之一。假设几何布朗运动,用如下等式描述股票回报方差 V V V 的随机变动情况:
d V V = α d t + ξ d W , V = σ 2 \frac{dV}{V}=\alpha dt+\xi dW,V=\sigma^2 VdV=αdt+ξdW,V=σ2
参数 ξ \xi ξ 表示方差的波动率
引入均值回归条件
Ornstein-Uhlenbeck 过程是传统上用来描述均值回归随机变量的过程。假设有一个均值回归过程 Y Y Y ,Ornstein-Uhlenbeck 随机微分方程的表达式如下:
d Y = α ( m − Y ) d t + β d W dY=\alpha(m-Y)dt+\beta dW dY=α(m−Y)dt+βdW
α , β , m \alpha,\beta,m α,β,m 是非负常数, d W dW dW 表示布朗运动,均值为0。如果用 Y Y Y 表示该均值回归流程当前的水平,那么 Y Y Y 发生变动之后的预期值就是:
E [ d Y ∣ Y ] = α ( m − Y ) d t E[dY|Y]=\alpha(m-Y)dt E[dY∣Y]=α(m−Y)dt
m m m 表示 Y Y Y 的长期均值。当 Y Y Y 大于 m m m 时, E [ d Y ∣ Y ] E[dY|Y] E[dY∣Y] 为负数,预期 Y Y Y 会下降,反之上升
首先假设没有随机变量( β = 0 \beta=0 β=0),于是:
d Y = α ( m − Y ) d t Y t = m + ( Y 0 − m ) e − α t dY=\alpha(m-Y)dt\\ Y_t=m+(Y_0-m)e^{-\alpha t} dY=α(m−Y)dtYt=m+(Y0−m)e−αt
其中 Y 0 Y_0 Y0 表示 Y Y Y 在 t = 0 t=0 t=0 时的初始状态,当 t t t 很大时, e − α t → 0 e^{-\alpha t}\to0 e−αt→0, Y t Y_t Yt 也会趋近于 m m m。在没有随机变量时,长期来看,不管初始值多少, Y Y Y 都会收敛至均值 m m m
假设 Y Y Y 从 Y 0 Y_0 Y0 回归至均值 m m m 需要的时间是 t t t,我们可以计算半衰期 t 1 / 2 t_{1/2} t1/2,其必须满足:
Y 0 − 1 2 ( Y 0 − m ) = m + ( Y 0 − m ) e − α t 1 / 2 1 2 ( Y 0 − m ) = ( Y 0 − m ) e − α t 1 / 2 Y_0-\frac{1}{2}(Y_0-m)=m+(Y_0-m)e^{-\alpha t_{1/2}}\\ \frac{1}{2}(Y_0-m)=(Y_0-m)e^{-\alpha t_{1/2}} Y0−21(Y0−m)=m+(Y0−m)e−αt1/221(Y0−m)=(Y0−m)e−αt1/2
求解得:
t 1 / 2 = 1 α ln ( 2 ) t_{1/2}=\frac{1}{\alpha}\ln(2) t1/2=α1ln(2)
这就是不存在随机变量时的半衰期,它跟 α \alpha α 成反比例关系。 α \alpha α 值越大,均值回归越快。如果波动率是随机变量,那么回归到均值的半衰期可能会更长或更短一些
对于随机Ornstein-Uhlenbeck过程( β ≠ 0 \beta\neq0 β=0),可以证明下式的解:
d Y = α ( m − Y ) d t + β d W dY=\alpha(m-Y)dt+\beta dW dY=α(m−Y)dt+βdW
为:
Y t = m + ( Y 0 − m ) e − α t + β ∫ 0 t e − α ( t − s ) d W s Y_t=m+(Y_0-m)e^{-\alpha t}+\beta\int_0^te^{-\alpha(t-s)}dW_s Yt=m+(Y0−m)e−αt+β∫0te−α(t−s)dWs
为了更好理解 Y Y Y 的变动,来看 Y t ˉ \bar{Y_t} Ytˉ 的行为特征, Y t ˉ \bar{Y_t} Ytˉ 表示 Y Y Y 在 t t t 时刻的平均值,计算的样本是前期所有的增量 d W s dW_s dWs。根据上式,由于每个布朗运动的增量均值都等于0,于是有:
Y t ˉ = m + ( Y 0 − m ) e − α t \bar{Y_t}=m+(Y_0-m)e^{-\alpha t} Ytˉ=m+(Y0−m)e−αt
所以 Y Y Y 在 t t t 时刻的平均值是确定的,等于 β = 0 \beta=0 β=0 时的解
在布朗运动过程中,每一个扰动都是独立的增量,因此我们也可以计算 Y t Y_t Yt 的方差。只要 s ≠ u s\neq u s=u,就存在 d W s d W u = 0 dW_sdW_u=0 dWsdWu=0。但是当 s = u s=u s=u 时, d W s d W u dW_sdW_u dWsdWu 就与 d u 2 du^2 du2 成正比。该关系式也可以用 Dirac delta 函数简洁地表达出来:
d W s d W u = δ ( u − s ) d s d u dW_sdW_u=\delta(u-s)dsdu dWsdWu=δ(u−s)dsdu
因此:
V a r [ Y t ] = E [ ( Y t − Y t ˉ ) 2 ] = β 2 ∫ 0 t ∫ 0 t e − α ( t − s ) e − α ( t − u ) d W s d W u = β 2 ∫ 0 t ∫ 0 t e − α ( 2 t − s − u ) δ ( u − s ) d s d u = β 2 ∫ 0 t e − 2 α t e 2 α u d u = β 2 2 α ( 1 − e − 2 α t ) Var[Y_t]=E[(Y_t-\bar{Y_t})^2]=\beta^2\int_0^t\int_0^te^{-\alpha(t-s)}e^{-\alpha(t-u)}dW_sdW_u\\=\beta^2\int_0^t\int_0^te^{-\alpha(2t-s-u)}\delta(u-s)dsdu=\beta^2\int_0^te^{-2\alpha t}e^{2\alpha u}du\\=\frac{\beta^2}{2\alpha}(1-e^{-2\alpha t}) Var[Yt]=E[(Yt−Ytˉ)2]=β2∫0t∫0te−α(t−s)e−α(t−u)dWsdWu=β2∫0t∫0te−α(2t−s−u)δ(u−s)dsdu=β2∫0te−2αte2αudu=2αβ2(1−e−2αt)
当 t t t 很小时, e − 2 α t ≈ ( 1 − 2 α t ) e^{-2\alpha t}\approx(1-2\alpha t) e−2αt≈(1−2αt),于是 V a r [ Y t ] ≈ β 2 t Var[Y_t]\approx\beta^2t Var[Yt]≈β2t。当 t t t 很小时, Y Y Y 的方差会随着时间的增加成近似线性增长关系,这跟在标准布朗运动中是一样的
当 t t t 不是很小的时候,Ornstein-Uhlenbeck过程中的方差就完全不一样了。当 t t t 趋于正无穷的时候,我们有
lim t → ∞ V a r [ Y t ] = β 2 2 α \lim_{t\to\infty}Var[Y_t]=\frac{\beta^2}{2\alpha} t→∞limVar[Yt]=2αβ2
收敛至常数 β 2 2 α \dfrac{\beta^2}{2\alpha} 2αβ2,均值回归的目的就是约束 Y Y Y 的变动范围。随着均值回归中的 α \alpha α 不断增加, Y Y Y 的变动范围不断收窄
针对一些随机波动率模型的调查
大部分随机波动率模型都假设股票价格服从传统的几何布朗运动:
d S S = μ d t + σ d Z \frac{dS}{S}=\mu dt+\sigma dZ SdS=μdt+σdZ
如果波动率 σ \sigma σ 是常数,就不存在微笑曲线。要使波动率既是随机变量又服从均值回归,最简单的办法就是用Ornstein-Uhlenbeck 方程:
d σ = α ( m − σ ) d t + β d W d\sigma=\alpha(m-\sigma)dt+\beta dW dσ=α(m−σ)dt+βdW
方差 V V V 也可以用类似的方程式表达:
d V = α ( m − V ) d t + β d W dV=\alpha(m-V)dt+\beta dW dV=α(m−V)dt+βdW
上述两式的问题在于,允许波动率和方差为负数。避免出现这个问题的办法就是,在方差逐步下降到 0 的过程中,令方差的方差随方差线性递减,也就是:
d V = α ( m − V ) d t + β V d W dV=\alpha(m-V)dt+\beta VdW dV=α(m−V)dt+βVdW
另一个方法就是选择Heston模型:
d V = α ( m − V ) d t + β V d W dV=\alpha(m-V)dt+\beta\sqrt{V}dW dV=α(m−V)dt+βVdW
此处,方差的方差随方差的平方根递减。这个模型的优势在于可求得解析值,因此非常流行
所有这些不同版本的随机波动率模型中,都引入了随机变量 S S S 和 σ \sigma σ,这两个变量均服从维纳过程,其变动用 d Z dZ dZ 和 d W dW dW 表示。在标准 BSM 模型中, σ \sigma σ 是独立变量,跟 S S S 之间没有相关性。在局部波动率模型中, σ \sigma σ 是一个由 S S S 决定的函数。在随机波动率模型中, S S S 和 σ \sigma σ 之间的相关系数更为灵活。我们可以用布朗运动的参数来描述二者之间的相关系数, d Z dZ dZ 和 d W dW dW 之间的相关系数 ρ \rho ρ 可以表示为:
d Z d W = ρ d t dZdW=\rho dt dZdW=ρdt
几乎所有的随机波动率模型都假设 ρ \rho ρ 是一个常数
风险中性估值及随机波动率模型
要在风险中性的条件下对期权进行估值,我们就需要在每一个瞬时进行对冲,以消除期权的风险。要做到这点,除非市场上有足够多的证券可以用来对冲,以应对每个瞬间可能出现的所有状态。如果期权已经被完全对冲了,那么对冲组合在每个瞬间的回报都是无风险收益率,这样就可以避免出现套利机会
在标准二叉树模型中,每个节点只有两种可能性:上行或下行。在上行阶段,股票价格会上升至 S u S_u Su。在下行阶段,股票价格会下跌至 S d S_d Sd。在BSM模型假设条件中,如果标的股票价格服从随机流程,我们就可以用股票和无风险债券构建两个状态依赖的Arrow-Debreu证券, Π u , Π d \Pi_u,\Pi_d Πu,Πd,分别对应两种损益状态,如下图所示:
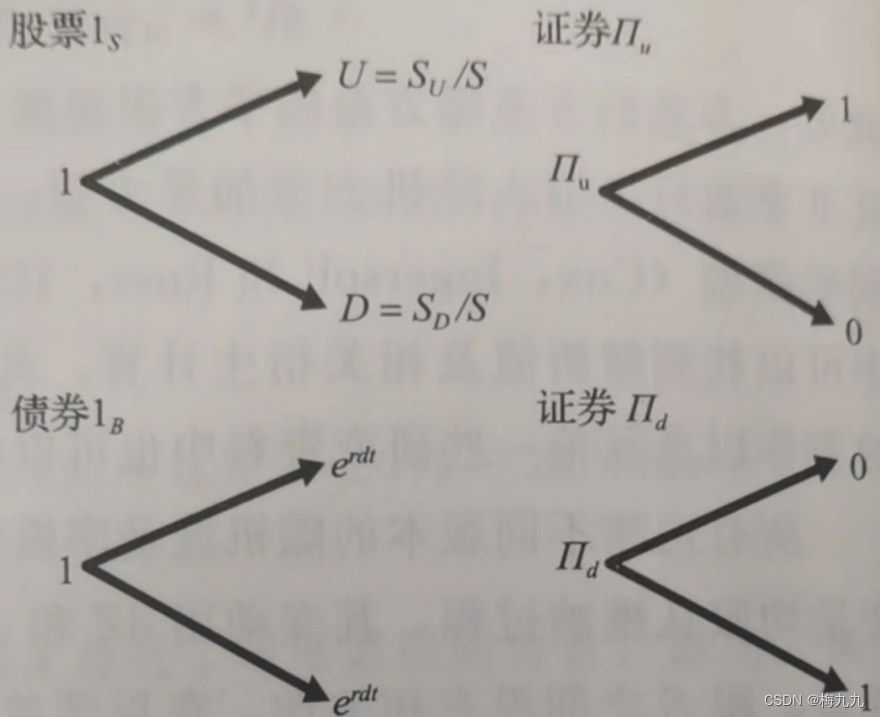
根据当前的股票和债券的价格,我们就可以知道这些证券的价格,进而可以计算任何衍生工具在一个时间段之后的特定损益;我们也可以用这种方法对标准期权进行估值,这只是一种特例。我们可以用Arrow-Debreu证券构成的组合来完全复制一个期权,确保复制组合在两种状态下的损益都跟期权一样。因此,股票的预期回报本身跟期权价值是没有相关性的
现在扩展这个二叉树模型,允许股票价格和波动率都服从随机流程。波动率也存在两种可能性, σ u , σ d \sigma_u,\sigma_d σu,σd,参数变动情况如下图所示:
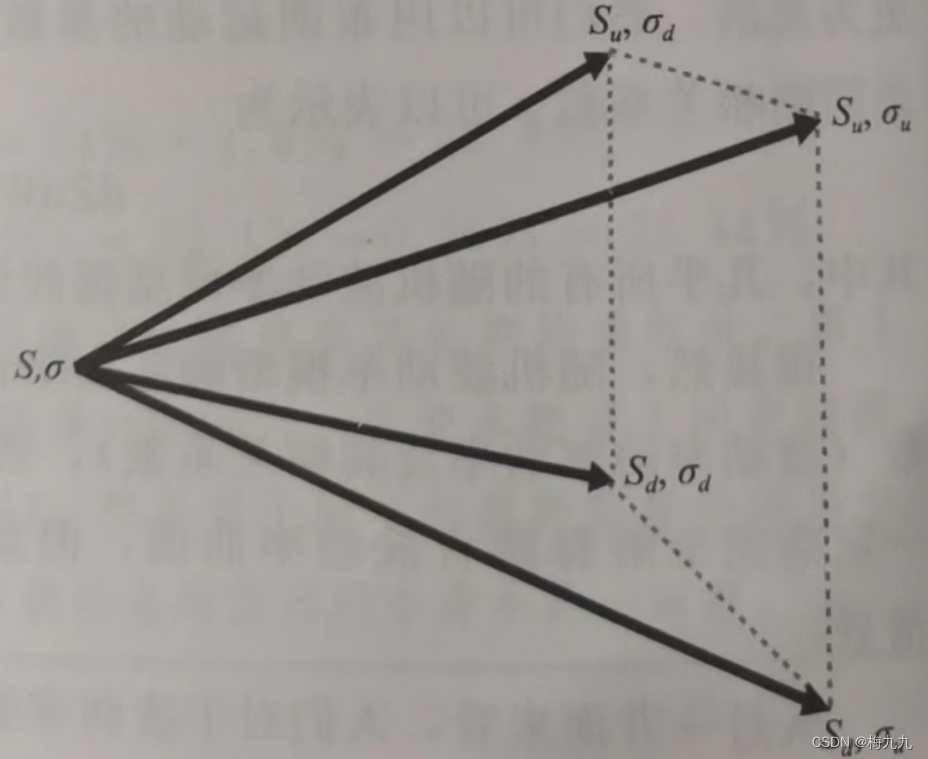
从任意节点出发,一共可以扩散出4种可能路径,这就是我们常说的四项模型。要遵从无套利机会的原则对一个期权进行估值,我们需要4个Arrow-Debreu证券才行,每个证券只有在4种状态的特定某一种状态下时才会支付1美元,而在其他3种状态下都支付0。股票和无风险债券只是两种证券。此外也可以发现,我们还需要知道当前的波动率值、波动率的波动率以及波动率与股票价格之间的相关系数。如果我们知道了所有这些参数值,那么我们就可以知道,这4种状态下支付的1美元的现值是多少,也就可以知道在随机波动率条件下,如何对期权进行估值并进行对冲



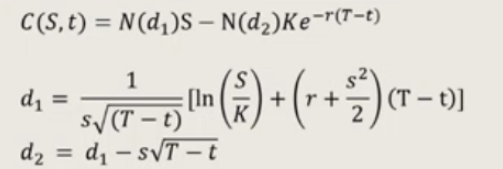

![[ CTF ]MISC flag](https://img-blog.csdnimg.cn/a49f9177579a4654baa956932c6255d1.png)