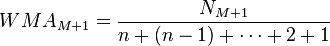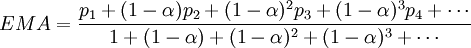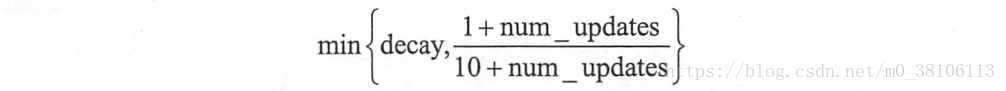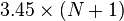Exponentially Weighted Moving Average(EWMA)指数加权移动平均是一种常用的序列数据处理方式，如下：
在时间 t, 根据实际的观测值（或量测值）我们可以求取 EWMA（t）如下：

EWMA(t ) = λY(t)+ ( 1-λ) EWMA(t-1) for t = 1, 2, ..., n.

* EWMA（t）：t时刻的估计值
* Y（t）： t 时间之量测值﹐
* n is the number of observations to be monitored including EWMA0
* λ ( 0 < λ< 1 ) ﹐表EWMA对于历史量测值之权重系数﹐其值越接近1，表对过去量测值的权重较低

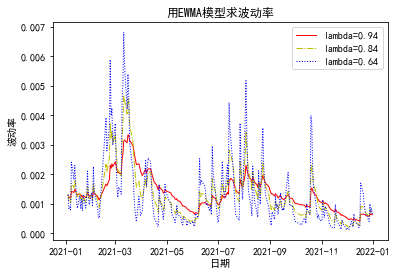
从另一个角度看， λ 决定了EWM A估计器跟踪实际数据突然发生变化的能力，即时效性，显然随着λ 增大，估计器的时效性就越强，反之，越弱;另一方面，由于 λ 的存在，EWMA还表现出一定的吸收瞬时突发的能力，这种能力称为平稳性。显然随着 λ 减小，估计器的平稳性增强，反之降低。

应用领域：
1. 金融和管理领域处理统计数据处理的一个常用工具
2. 在通信领域中，EWMA主要用于对网络的状态参数进行估计和平滑，例如在TCP 拥塞控制中EWMA被用来计算分组的往返时延( RTT ) ，在拥塞控制中的主动队列管理(AQM）技术中很多使用EWMA平滑估计拥塞指示参数( 如平均队长) 等参数

深入观察：
1. 从概率角度看，EWMA是一种理想的最大似然估计技术，它采用一个权重因子 λ 对数据进行估计，当前估计值由前一次估计值和当前的抽样值共同决定

2. 从信号处理角度看，EWMA可以看成是一个低通滤波器，通过控制 λ 值，剔除短期波动、保留长期发展趋势提供了信号的平滑形式

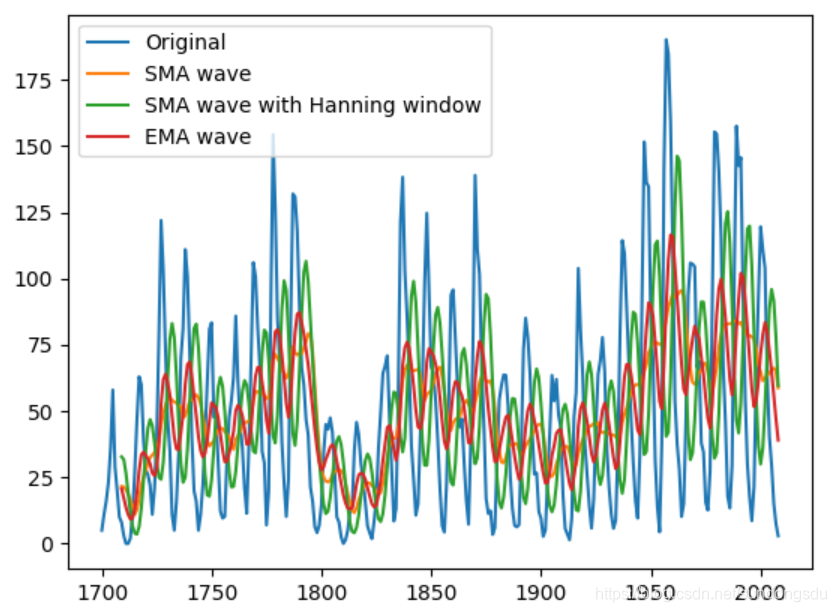
移动平均

移动平均，简称均线，是技术分析其中一种分析时间序列数据的工具。最常见的是利用股价、回报或交易量等变量计算出移动平均。

移动平均可抚平短期波动，将长线趋势或周期显现出来。数学上，移动平均可视为一种卷积。

简单移动平均

简单移动平均（Simple moving average, SMA）是之前n个数值的未作加权算术平均。例如，收市价的10日简单移动平均指之前10日收市价的平均数。设收市价为p₁至p_n，则方程式为：

$SMA = { p_1 + p_2 + \cdots + p_n \over n }$

当计算连续的数值，一个新的数值加入，同时一个旧数值剔出，所以无需每次都重新逐个数值加起来：

$SMA_{t1} = SMA_{t0} - {p_1 \over n} + {p_{n+1} \over n}$

在技术分析中，有几个n的数值较为普遍，如10日、40日、200日，视乎分析时期长短而定。投资者冀从移动平均线的图表中分辨出支持位或阻力位。

加权移动平均

加权移动平均（Weighted moving average, WMA）指计算平均时个别数据乘以不同数值，在技术分析中，n日WMA的最近期一个数值乘以n、次近的乘以n-1，如此类推，一直到0：

$WMA_{M} = { n p_{M} + (n-1) p_{M-1} + \cdots + 2 p_{M-n+2} + p_{M-n+1} \over n + (n-1) + \cdots + 2 + 1}$

WMA，N=15

由于WMA_{M + 1}与WMA_M的分子相差 $n p_{M+1} - p_{M} - \cdots - p_{M-n+1}$ ，假设 $p_{M} + p_{M-1} + \cdots + p_{M-n+1}$ 为总和_M：

总和_M+1 = 总和_M + p_{M + 1} − p_{M − n + 1}

分子_M+1 = N_{M + 1} = 分子_M + np_{M + 1} − 总和_M

$WMA_{M+1} = { N_{M+1} \over n + (n-1) + \cdots + 2 + 1}$

留意分母为三角形数，方程式为 $n(n+1)\over2$

右图显示出加权是随日子远离而递减，直至递减至零。

指数移动平均

EMA，N=15

指数移动平均（Exponential Moving Average, EMA或EWMA）是以指数式递减加权的移动平均。各数值的加权而随时间而指数式递减，越近期的数据加权越重，但较旧的数据也给予一定的加权。右图是一例子。

加权的程度以常数α决定，α数值介乎0至1。α也可用N来代表： $\alpha={2\over{N+1}}$ ，所以，N=19代表α=0.1。

设时间t的数值为Y_t，而时间t的EMA则为S_t，计算时间t≥2是方程式为：^[1]

$S_{t} = \alpha \times Y_{t-1} + (1-\alpha) \times S_{t-1}$

设p=昨日(t0)价格，今日(t1)EMA的方程式为：

$EMA_{t1} = EMA_{t0} + \alpha \times (p - EMA_{t0})$

将EMA_t0分拆开来如下：

$EMA = { p_1 + (1-\alpha) p_2 + (1-\alpha)^2 p_3 + (1-\alpha)^3 p_4 + \cdots \over 1 + (1-\alpha) + (1-\alpha)^2 + (1-\alpha)^3 + \cdots }$

理论上这是一个无穷级数，但由于1-α少于1，各项的数值会越来越细，可以被忽略。分母方面，若有足够多项，则其数值趋向 1/α。

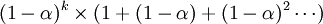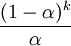假设k项及以后的项被忽略，即 $(1-\alpha)^k + (1-\alpha)^{k+1} + \cdots$ ，重写后可得 $(1-\alpha)^k \times (1 + (1-\alpha) + (1-\alpha)^2 \cdots)$ ，相当于 ${(1-\alpha)^k \over \alpha}$ 。所以，若要包含99.9%的加权，解方程 $k={ \log (0.001 \times \alpha) \over \log (1-\alpha)}$ 即可得出k。由于当N不断增加， $\log\,(1-\alpha)$ 将趋向 $-2 \over N+1$ ，简化后k大约等于 $3.45\times(N+1)$ 。