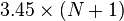最近我们被客户要求撰写关于波动率的研究报告，包括一些图形和统计输出。
从广义上讲，复杂的模型可以实现很高的预测准确性。
但是您的读者需要快速理解。他们没有意愿或时间去处理任何太乏味的事情，即使它可以稍微准确一些。简单性是商业中非常重要的模型选择标准。在多元波动率估计中，最简单的方法是使用历史协方差矩阵。但这太简单了，我们已经知道波动性是随时间变化的。您经常看到从业者使用滚动标准差来模拟随时间变化的波动率。它可能不如其他最先进的方法准确， 但它实现起来非常简单，也很容易解释。
什么是滚动窗口估计。如果我们有一个包含 5 个观察值的向量并且我们使用 2 个窗口，那么用于估计的权重向量是 [0,0,0,0.5,0.5]。更进一步的做法是对更远的过去给予少一些权重，但要对最近的观察样本给予更大的权重，比如权重向量 [0.05, 0.1, 0.15, 0.3, 0.4]。
根据低波动率跟着低波动率走，高波动率跟着高波动率走（波动率聚类）的典型事实，这个想法完全适合于多变量波动率预测。请考虑以下情况。
(1) 
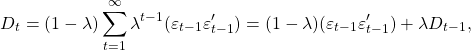
其中 
是协方差矩阵的当前估计，并且 
是基于过去直到时间段 t-1 的协方差矩阵。我们使用最简单的估计，即历史协方差矩阵，但增加了一些权重（
）到仅基于最近的观察估计的协方差矩阵。这真的很容易解释，几乎是一个行业标准。可以估计我们希望权重下降的速度，但您也可以根据一些先前的研究，将衰减参数估计为 0.94。
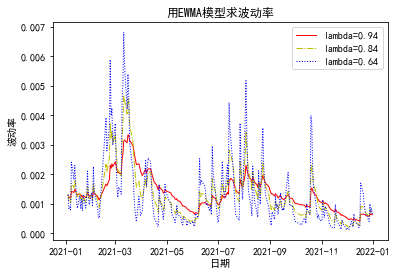
我绘制几个不同 lambda 值随时间变化的相关矩阵：
k <- 10 # 几年前？end<- format(Sys.Date(),"%Y-%m-%d")start<-format(Sys.Date() - (k*365),"%Y-%m-%d")dat0 = getSymbolsfor (i in 1:l){da0 = getSymbols(sym[i])ret[2:n,i]
}EWMAplot
legend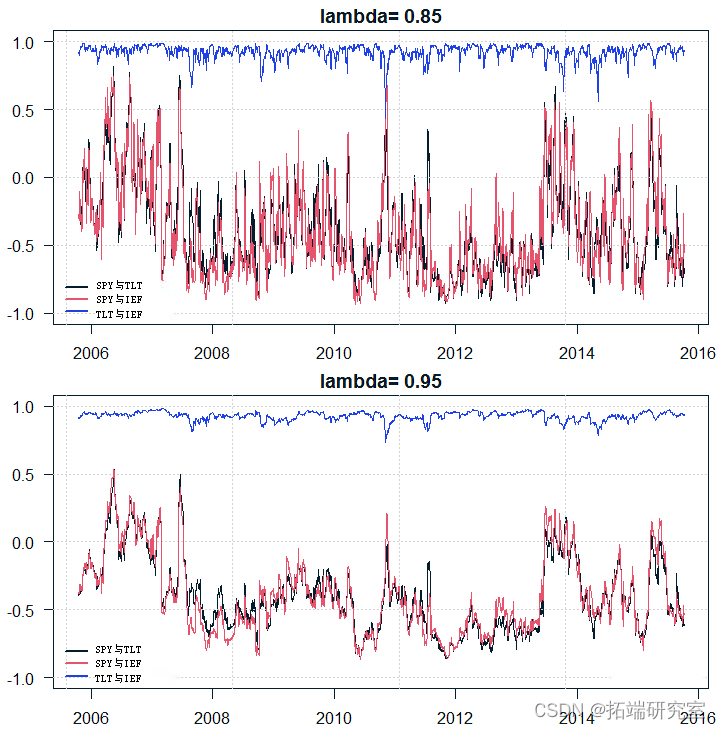 
您可以看到，如果您为最后一次观察样本分配 15% 的权重，您会得到一些不稳定的估计。仅 5% (lambda = 0.95) 的权重给出了更平滑的估计，但可能不太准确。
除了简单之外，另一个重要的优点是不需要关心可逆性，因为在每个时间点上，估计值只是两个有效的相关矩阵的加权平均数。还有，你可以将这种方法应用于任何金融工具，不管是流动的还是非流动的，这是它受欢迎的另一个原因。
EWMA <-function {## ＃＃＃输入。## factors N x K的数字因素数据。数据是类data.frame## N是时间长度，K是因素的数量。 ## lambda 标量。指数衰减系数在0和1之间。## return.cor 如果是TRUE则返回EWMA相关矩阵##输出。 covewma = array
covf = var(factors) # 时间=0时的无条件方差为EWMAmfas <- apply(factors,2, mean)for (i in 2:t.factor) {
FF
cov.f.ewma
}}if(return.cor) {cewma
for (i in 1:dim[1]) {corewma= covr(coewm[i, ,])这个函数不适合用于样本外的预测。原因是我们向样本协方差矩阵收缩，而协方差矩阵是基于全样本的，在样本结束前我们还不知道。在现实的设置中，我们只能使用到我们希望预测的那一点为止的信息。随后，我改变了原始函数，加入了一个额外的参数（用于估计协方差矩阵的初始窗口长度）。然后，初始协方差矩阵的取值只使用到预测时为止的信息，标准化也是如此。修改后的新函数如下
EWMAs <- function{# 调整了样本外的协方差预测## 输入。##因素N x K数字因素数据。数据是类data.frame## N是时间长度，K是因素的数量。 ## la指数衰减因子在0和1之间。## retu 逻辑的，如果是TRUE则返回EWMA相关矩阵##输出。 coa = array(,c(t.cor,k.tor,k.aor))fas <- applycovf = var
co.ewa[(wind-1),,] = (1-lad)*FF + ada*cov.ffor (i in wind : t.factor) {covf = var# 到t的无条件方差。FF = (fators[i,]- mctors) %*% t(factors[i,]- mfcrs)coma[i,,] = (1-laa)*FF + laba*coma[(i-1),,]for (i in wn:dim) {orma[i, , ] = covr(owma[i, ,])
