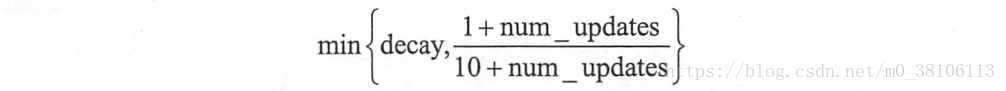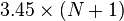最近我们被客户要求撰写关于风险价值的研究报告，包括一些图形和统计输出。

此示例说明如何使用三种方法估计风险价值 (VaR) 并执行 VaR 回测分析。这三种方法是：

正态分布
历史模拟
指数加权移动平均线 (EWMA)

视频：风险价值VaR原理与Python蒙特卡罗Monte Carlo模拟计算投资组合实例

风险价值VaR原理与Python蒙特卡罗Monte Carlo模拟计算投资组合实例

，时长10:03

风险价值是一种量化与投资组合相关的风险水平的统计方法。VaR 衡量指定时间范围内和给定置信水平的最大损失量。

回测衡量 VaR 计算的准确性。使用 VaR 方法，计算损失预测，然后与第二天结束时的实际损失进行比较。预测损失和实际损失之间的差异程度表明 VaR 模型是低估还是高估了风险。因此，回测回顾数据并有助于评估 VaR 模型。

本示例中使用的三种估计方法在 95% 和 99% 的置信水平下估计 VaR。

加载数据并定义测试窗口

加载数据。本例中使用的数据来自标准普尔指数从 1993 年到 2003 年的时间序列收益率。

tik2rt(sp);

将估计窗口定义为 250 个交易日。测试窗口从 1996 年的第一天开始，一直持续到样本结束。


WinSze = 250;

对于 95% 和 99% 的 VaR 置信水平。

p = [0.05 0.01];

这些值意味着分别有至多 5% 和 1% 的概率发生的损失将大于最大阈值（即大于 VaR）。

使用正态分布方法计算 VaR

对于正态分布法，假设投资组合的损益呈正态分布。使用此假设，通过将每个置信水平的z分数乘以收益率的标准差来计算 VaR 。由于 VaR 回溯测试对数据进行追溯，因此“今天”的 VaR 是根据过去N = 250 天（但不包括“今天”）的收益率值计算得出的。


for t = TtWnowi = t - TsWidoSrt + 1;Esationdw = t-EtiWinwSze:t-1;gma = std(Returns(tmWinow));Noa95(i) = -Zscre(1)*Sima;Nrml99(i) = -Zsore(2)*Sigma;
endplot(DaeRtuns(TsWidw),[Nrm95 oma99])

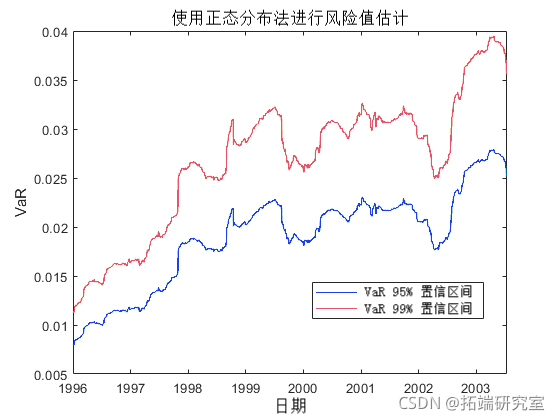
正态分布方法也称为参数 VaR，因为它的估计涉及计算收益率标准差的参数。正态分布方法的优点是简单。然而，正态分布方法的弱点是假设收益率是正态分布的。正态分布方法的另一个名称是方差-协方差方法。

使用历史模拟方法计算 VaR

与正态分布方法不同，历史模拟 (HS) 是一种非参数方法。它不假设资产收益的特定分布。历史模拟通过假设过去的损益可以作为下一个收益期的损益分配来预测风险。“今天”的 VaR 计算为“今天” 之前最后N 次收益率的 第 p个分位数。


for t = Tstidowi = t - Tsidwtt + 1;Htrl95(i) = -qate(X,pVR(1));Hii99(i) = -qatie(X,pVaR(2));fiure;
plot(Dtr(Ttow),[Hic95 Hstrl99])

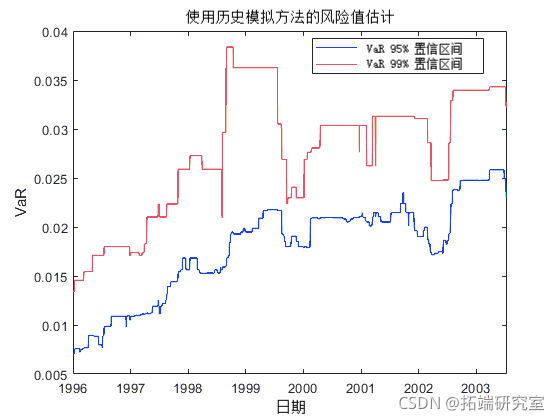
从上图可以看出，历史模拟曲线具有分段不变的轮廓。其原因是，在极端事件发生之前，量值在几天内不会发生变化。因此，历史模拟方法对波动率的变化反应缓慢。

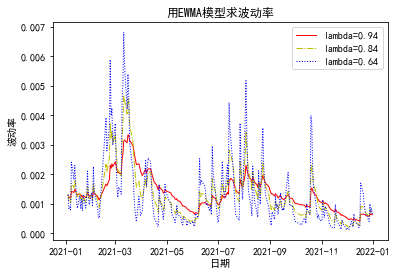
使用指数加权移动平均法 (EWMA) 计算 VaR

前两个 VaR 方法假设所有过去的收益率都具有相同的权重。指数加权移动平均 (EWMA) 方法分配不相等的权重，尤其是指数递减的权重。最近的收益率具有更高的权重，因为它们对“今天”收益率的影响比过去更远的收益率更大。大小估计窗口上的 EWMA 方差公式 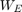$ W_E $ 是：

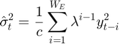
$\hat{\sigma}^2_t=\frac{1}{c}\sum_{i=1}^{W_E}\lambda^{i-1} y^2_{ti}$

$c$ 是归一化常数：

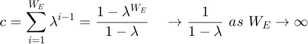
$c=\sum_{i=1}^{W_E}\lambda^{i-1} = \frac{1-\lambda^{W_E}}{1-\lambda}\quad\rightarrow \frac{1 }{1-\lambda} ~ as ~ W_E\rightarrow\infty$

为方便起见，我们假设一个无限大的估计窗口来近似方差：

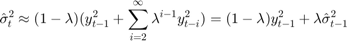
$\hat{\sigma}^2_t\approx(1-\lambda)(y^2_{t-1}+\sum^{\infty}_{i=2}\lambda^{i-1}y ^2_{ti})=(1-\lambda)y^2_{t-1}+\lambda\hat{\sigma}^2_{t-1}$

实践中经常使用的衰减因子的值为0.94。这是本示例中使用的值。

启动 EWMA 设置标准偏差。

Laa = 0.94;for i = 2 : (Tsart-1)Sm2(i) = (1-Labda) * Rts(i-1)^2 + Lama * m2(i-1);

在测试窗口中使用 EWMA 来估计 VaR。


for t = TeWioEWMA95 (k) = -Zscre(1)*Sima;EWMA99(k) = -Zsoe(2)*Siga;
endplot(DR,[EWMA95 EWMA99])

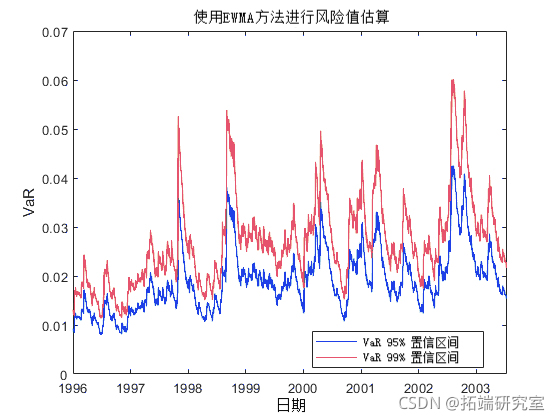
在上图中，EWMA 对大（或小）收益率时期的反应非常迅速。

VaR回测

在本示例的第一部分中，使用三种不同的方法和两种不同的 VaR 置信水平在测试窗口上估计了 VaR。VaR 回测的目标是评估 VaR 模型的性能。95% 置信度的 VaR 估计值仅在大约 5% 的时间内被违反。VaR 失败的集群表明缺乏跨时间的独立性，因为 VaR 模型对不断变化的市场条件反应缓慢。

VaR 回测分析中常见的第一步是将收益率和 VaR 估计值绘制在一起。在 95% 的置信水平上绘制所有三种方法，并将它们与收益率进行比较。

Rtnet = Rrns(Tstnow);
DesTst   = Das(TsWnow);
fige;
plot

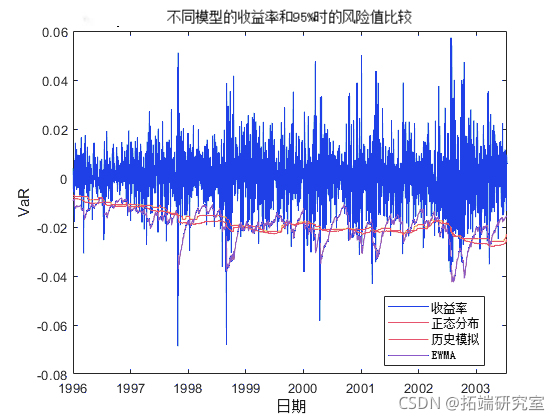
为了突出不同的方法如何对不断变化的市场条件做出不同的反应，您可以放大收益率值发生巨大和突然变化的时间序列。例如，大约在 1998 年 8 月：

Zm   = (Da >= da(1998,8,5)) & (D <= da(1998,10,31);br(D,);for i = 1 : sze(Vata,2)sts(D-0.5,VaRData(:,i),VaFt{i});plot(D(IN95),-N(nN95)

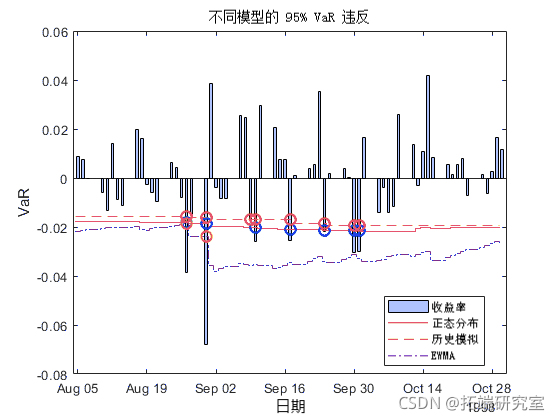
当收益为负 VaR 时，就会发生 VaR 失败。仔细观察 8 月 27 日至 8 月 31 日，会发现收益率显着下降。从 8 月 27 日起，EWMA 更密切、更准确地跟踪收益率趋势。因此，与正态分布方法（7次失败，蓝色）或历史模拟方法（8次失败，红色）相比，EWMA 的 VaR 失败（2)次失败，紫色）较少。

除了可视化工具，您还可以使用统计测试进行 VaR 回测。在此示例中，首先比较正态分布方法在 95% 和 99% VaR 水平下的不同测试结果。

bctet(etet,[Nrml95 Noml99]);
summary

摘要报告显示观察到的水平与定义的 VaR 水平足够接近。95% 和 99% VaR 水平至多具有期望失败，其中 N 是观察次数。失败率表明 VaR 水平在范围内，而 VaR 水平不精确并且低估了风险。运行所有支持的测试 (1-VaR_level) x N

test(vt)

95%的VaR通过了测试，如二项式和失败比例测试（TL、BIN和POF列）。99%的VaR没有通过这些相同的测试，如拒绝结果所示。在条件覆盖率独立性和间隔时间独立性（ci和tbfi列）中，两个置信度都被拒绝。这个结果表明，VaR的违反不是独立的，可能在短时间内有多次失败的时期。另外，一次失败可能会使其他失败在随后的日子里更有可能发生。

在两个 VaR 置信水平下对三种方法的投资组合运行相同的测试。

 rbackest

结果和之前的结果差不多，在95%的水平上，结果基本可以接受。然而，在 99% 水平的结果通常是拒绝。关于独立性，大多数测试通过了条件覆盖独立性测试，连续几天测试独立性。请注意，所有测试都失败了独立性测试之间的时间间隔，它考虑了所有失败之间的时间。这个结果表明所有方法都存在独立性假设的问题。

为了更好地了解这些结果如何在市场条件下发生变化，请查看 2000 年和 2002 年的 95% VaR 置信水平。

n00 = yar(aet) == 2000);

I22 = (ea) == 2002);
v202 = rbks(RtrTt(n202

2000年，这三种方法都通过了所有的测试。但是，2002 年的测试结果大多是所有方法都被拒绝。EWMA 方法似乎在 2002 年表现更好，但所有方法都未能通过独立性测试。

要更深入地了解独立性测试，请查看条件覆盖独立性和失败间隔时间独立性2002 年的测试详细信息。运行各个测试功能。

cci

在 CCI 测试中，知道在时间t -1没有失败的情况下，在时间t发生失败的概率 p 由下式给出01

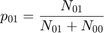
$p_{01} = \frac{N_{01}}{N_{01}+N_{00}}$

在时间t发生失败的概率 p ，知道在时间t -1发生失败，由下式给出11

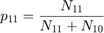
$p_{11} = \frac{N_{11}}{N_{11}+N_{10}}$

从测试结果中的N00, N10, N01, N11列来看，三种方法的p 值 01都在 5% 左右，而p 值 11 都在 20% 以上。因为有证据表明一个失败之后出现另一个失败的频率远高于 5%，所以这个 CCI 测试失败了。

在失败间隔时间独立性测试中，查看失败间隔时间分布的最小值、最大值和四分位数，在TBFMin、 TBFQ1、 TBFQ2、 TBFQ3、列中 TBFMax。

tbfi

对于 95% 的 VaR 水平，您预计失败之间的平均时间为 20 天，或每 20 天发生一次失败。但是，对于这三种方法，2002 年的失败间隔时间的中位数介于 5 到 7.5 之间。该结果表明，在一半的情况下，连续两次失败发生在 5 到 7 天内，比期望的 20 天要频繁得多。因此，会发生更多的测试失败。对于正态方法，第一个四分位数是 1，这意味着 25% 的失败发生在连续几天。