#tushare ID：474220
指数移动平均（Exponential Moving Average, EMA或EWMA）是以指数式递减加权的移动平均。各数值的加权而随时间而指数式递减，越近期的数据加权越重，但较旧的数据也给予一定的加权。加权的程度以常数λ决定，λ数值介乎0至1。
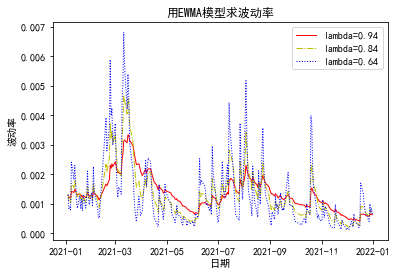
金融资产的波动率对理解资产价格的动态特征是是极为重要的。历史波动率是过去一段时间标的资产价格的波动程度，历史波动率方法是利用历史数据预测资产的波动率。EWMA模型是常用的历史波动率方法，下面我们通过python程序来展示如何实现EWMA模型对历史波动率的估计。
本次使用的数据来自与Tushare平台，有较为全面的金融数据可供使用，通过数据接口调用数据简单快捷，可以通过在终端利用命令pip install tushare安装该库并进行调用。

1.首先我们导入必要的库

import numpy as np
import scipy.io as scio
import datetime
from scipy import stats
import matplotlib.pyplot as plt
import scipy.stats as st
import tushare as ts
#正常显示画图时出现的中文和负号
plt.rcParams["font.sans-serif"]=["SimHei"]
plt.rcParams["axes.unicode_minus"] = False

2.初始化pro接口。token可以在https://tushare.pro/上注册后获得。

pro = ts.pro_api('your token')

3.提取数据。本次我们调用的是600809.SH这支股票2021年的日线数据，同时并对数据进行一些预处理。

data = pro.daily(ts_code='600809.SH', start_date='20210101', end_date='20211231')
data = data.sort_values(by=['trade_date']).reset_index(drop=True)

4.提取收益率并格式化时间，为下一步计算做好准备

date = np.array(pd.to_datetime(data['trade_date']))
r = np.array(data['pct_chg'])/100

 5.计算波动率，并绘制各种lambda下的波动率图形。

lamda=0.94
n=len(r)
s11=[np.var(r[0:9])]
for i in range(1,n):s11=np.append(s11,lamda*s11[i-1]+(1-lamda)*r[i-1]**2)
lambda2=0.84
s12=[np.var(r[0:9])]
for i in range(1,n):s12=np.append(s12,lambda2*s12[i-1]+(1-lambda2)*r[i-1]**2)
lambda3=0.64
s13=[np.var(r[0:9])]
for i in range(1,n):s13=np.append(s13,lambda3*s13[i-1]+(1-lambda3)*r[i-1]**2)
plt.xlabel("日期")
plt.ylabel("波动率")
plt.title("用EWMA模型求波动率")
plt.plot(date,s11,'r-',label='lambda=0.94',linewidth=1)
plt.plot(date,s12,'y-.',label='lambda=0.84',linewidth=1)
plt.plot(date,s13,'b:',label='lambda=0.64',linewidth=1)
plt.legend()
plt.show()