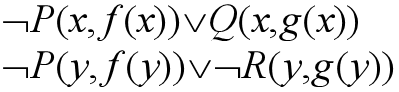本次，我对前面所学的算符进行一定的拓展并对接下来的量子信息的学习做一些铺垫。

一.些概念的复习和拓展

   在前面，我对量子计算的一些概念进行了简单的讲解，而且对一些概念描述的并不完整，所以此次我会完善一下厄米算符、幺正算符以及对易和反对易的知识点，并看看能否以我现在的水平去拓展一些知识。

1.算符

• 厄米算符
     对于希尔伯特空间 H 中的任意线性算符 A，在 H 中存在唯一的线性算符 A ^†⁡，使得对于在该希尔伯特空间中的所有矢量|$\alpha$⟩和|$\beta$⟩满足以下关系：⟨$\alpha$| A $\beta$⟩=⟨A ⁡^†⁡ $\alpha$|$\beta$⟩，则 A ^†⁡为 A 的伴随（或者 A =A ⁡^†⁡，’†’⁡表示共轭转置）
     性质：⟨A $\alpha$| $\beta$⟩=⟨$\alpha$|A ⁡^†⁡ $\beta$⟩，( AB )^†⁡=B^†⁡A^†⁡,( A + B )^†⁡=A ^†⁡+ B ^†⁡,(A^†⁡)^†⁡=A
  (1)量子力学中,可以观测的物理量要用厄米算符来表示。
  (2)在任何状状态下，厄米算符的本征值必为实数；
  (3)厄米算符是实对称矩阵在复空间的对应，从而也满足一些实对称矩阵的性质，比如不同的本征值对应的本征矢量相互正交。
  下面我开始计算一个二阶厄米算符 A 的本征值和本征矢量：
  

从而可以看到，这样一个厄米算符是不可以对角化的，有条件的也可以使用matlab算一下，很简单的：

• 幺正算符
      如果算符 U 存在如下关系：U U ^†⁡=U ^†⁡U =I，则 U 被称为幺正算符，可以很轻松地看出 U 与 U ^†⁡互逆.
     性质：两个算符的幺正算符也是幺正算符；幺正算符可以保持两个矢量的内积不变，是一种保留内积的有界运算符。现在对幺正算符的保留内积的性质进行证明：
  

    在学习有关量子计算的相关知识时，经常会看到有关幺正算符的资料，比如说，一个量子的物理系统演化是幺正的（或者说，为了方便研究，常常会要求它是幺正的），而波函数坍缩是一个非幺正的过程，再简单点说，量子力学中波函数的演化是么正的，但在测量中波函数是坍缩的。

2.对易和反对易

    定义运算：对于算符 A 和 B，[A,B]=AB - BA ，{A, B }=A B +B A.
若[A,B]=AB - BA，则称算符A和B对易，若{A, B }=A B +B A=0，则称算符 A 和 B 反对易。

二.有关量子信息学习的一些铺垫内容

1.薛定谔的猫

    想到薛定谔的猫，我就想到了四大神兽：芝诺的乌龟、拉普拉斯兽、麦克斯韦妖、薛定谔的猫。薛定谔的猫是一个思想实验，是指将一只猫关在装有少量镭和氰化物的密闭容器里。镭的衰变存在几率，如果镭发生衰变，会触发机关打碎装有氰化物的瓶子，猫就会死；如果镭不发生衰变，猫就存活。在没有打开这个密闭容器的情况下，猫会处于要死不活的叠加态，在打开了密闭容器的情况下，猫会处于要么死要么或的唯一状态下，比较有意思的说法是，打开密闭容器后，这只猫如果死了，它在另一个世界就一定活着（平行宇宙）。

2.EPR悖论

    EPR实验是爱因斯坦等人和玻尔就量子力学是否完备引发的一系列思想实验中的一个，爱因斯坦等人假设两个总自旋为0的粒子（或一个自旋为0的粒子衰变为两个粒子）在空间上分隔开来，分隔的距离非常大，大到对其中一个粒子进行物理操作而不会影响到另一个粒子。大概意思是，我们首先测量一个粒子A的位置，由此，那么另一个粒子B的位置也就确定下来了（相对位置），由于对这个粒子A的物理操作不会影响到另一个粒子B，那么同理接着去测量另一个粒子B的动量也就会得到粒子A的动量并且不会影响到粒子A，但是根据测不准原理，一个粒子的动量和位置不可以同时进行精确的测量，即在测量粒子A的位置时，粒子B的动量也无法测量了。从而只能得到下面两种结论的其中一个：
（1）存在即时的超距作用，在测量粒子A的位置的同时扰动了粒子B的动量；
（2）一个粒子的位置和动量本就同时存在，只不过量子力学描述的不够完备；
从而爱因斯坦得出量子力学不足以描述真实的世界的结论。

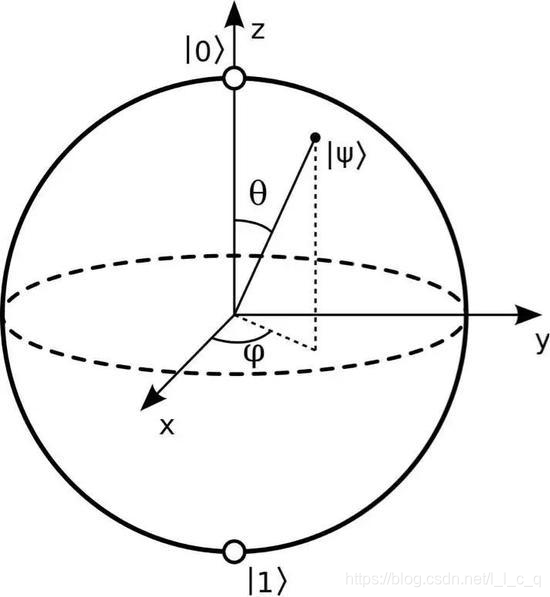
3.布洛赫球表示法

   布洛赫球提供了非常直观的单个量子比特纯状态可视化的几何表示,对于一个叠加态 |$\phi$⟩=$\alpha$|0⟩+$\beta$|1⟩,$\alpha$和$\beta$满足归一化要求，我们令$\alpha$=cos($\theta$/2)e^i$\delta$,$\beta$=sin⁡($\theta$/2)e^{i($\delta$+$\varphi$)}
⇒|$\phi$⟩=cos($\theta$/2)e^i$\delta$ |0⟩+sin($\theta$/2)e^{i($\delta$+$\varphi$)} |1⟩=e^i$\delta$ (cos($\theta$/2) |0⟩+sin($\theta$/2) e^i$\varphi$ |1⟩),然后将cos($\theta$/2) |0⟩+sin⁡($\theta$/2) e^i$\varphi$ |1⟩表现在球面上如下图，其中
0≤$\theta$≤$\pi$,0≤$\varphi$≤2$\pi$

并且

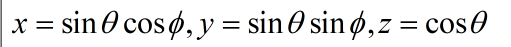
两个态矢在抽象意义上相互正交，但反映在布洛赫球面上却是$\pi$，是态矢在抽象意义上夹角为$\pi$/2的两倍，两个态矢在态空间的夹角总是它们在物理空间上夹角的1/2,布洛赫球面可以稍稍解释一下这种情形，但我仍然觉得有些许抽象,换一种说法就是，由于两个态要求正交，而正交规定为90度，要将平面的圆化为立体的球，推出来的|$\phi$⟩的表达式中只能是$\theta$/2，这样才能满足，角度变化范围在0到90度之间，而非0到180度，布洛赫球面我认为可以理解为一种工具。

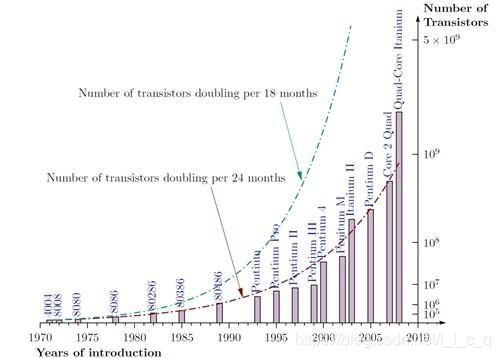
4.摩尔定律

    当价格不变时，集成电路上可容纳的元器件的数目，约每隔18-24个月便会增加一倍，性能也将
提升一倍。

    这也意味着，在将来我们不得不考虑在电路中产生的量子效应（当电路线宽小于0.1微米）

5.量子信息载体的微观特征

量子态相干性

   电子向右自旋和正电子向左自旋的状态是相关联的，这种关联的性质称作量子相干性.

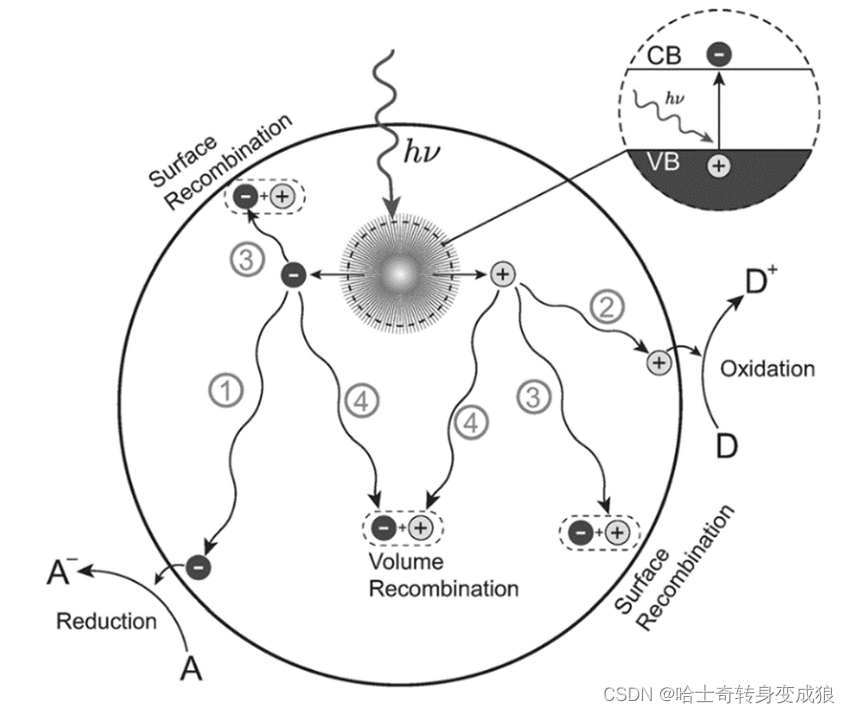
    相干源于波动，意为可以产生相互干涉，干涉只在两列波到某一个点的频率相同相等、振动方向相同或者相位差恒定的情况下产生。量子的相干性，指的大概就是量子的行为像波一样，量子的许多特性都来源于量子的相干性。而在实际生活中，最简单的例子就是光的干涉条件并没那么容易达成（或者说很容易受到影响而不再干涉），当相干性消失，即为退相干，下图展现的是光的干涉.

量子态纠缠性

    独立的系统相关联会产生一个不独立的系统，两个独立的系统会产生关联是源于它们的波函数里有着相同的物理量，从上图也可以看出，这样独立的系统是可以不止一个的，这些独立的系统相互关联、纠缠起来，它们成了一个整体，牵一发而动全身，这就是纠缠性。量子的纠缠性在量子通讯这一块大展宏图，理论上可以实现超高速的信息传送。

量子态叠加性

    对于两个量子态，我们用两个态矢量来表示它们的状态，从一个态矢量转变为另一个态矢量有着一个过程，在这个过程中，这个态矢量的状态不断发生变化。量子态的叠加性就体现在两个量子态构造的整个系统可以处于在这两个态间的任意一个态，简单来说可以处于这个态也可以处于那个态，搞不清楚究竟处于哪个态就是叠加态，叠加态是量子并行计算的物理基础。

量子不可克隆定理

    量子不可克隆定理是指量子力学中对任意一个未知的量子态进行完全相同的复制的过程是不可实
现的，

    量子不可克隆定理是说不能复制一个状态未知的系统，因为复制的过程会破坏它的状态，它构成了量子密码学的基础，因为量子不可克隆定理使得量子信息不能像经典信息那样可以被任意复制，这使得人们能够建立起绝对安全的量子密码系统。

本篇文章就此结束……