不同的卷积操作
- 本文所用样本
- 一般的卷积(常规的)
- 分组卷积
- 深度分离卷积
- 逐通道卷积(depthwise conv)
- 逐点卷积 (pointwise conv)
- 分组深度分离卷积
- 上面卷积总结
- 卷积的dilation
本文所用样本
x = t o r c h . z e r o s ( 5 , 5 , 4 ) x = torch.zeros(5,5,4) x=torch.zeros(5,5,4), 维度分别表示(w, h, channels)
import torch
x = torch.zeros(5,5,4)
print(x.size())
# torch.Size([5, 5, 4])
假设我们期望卷积后,样本的大小变为(3, 3, 10)
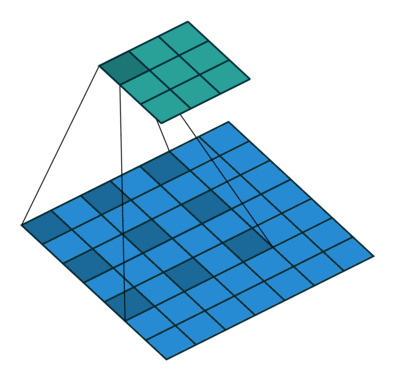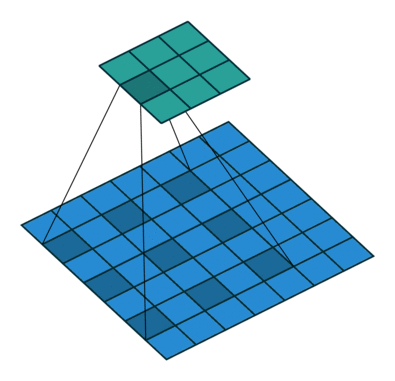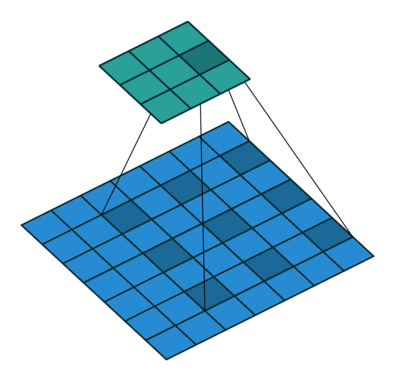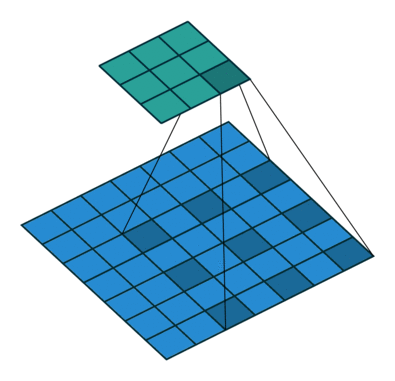
一般的卷积(常规的)
为方便理解,示意图如下:
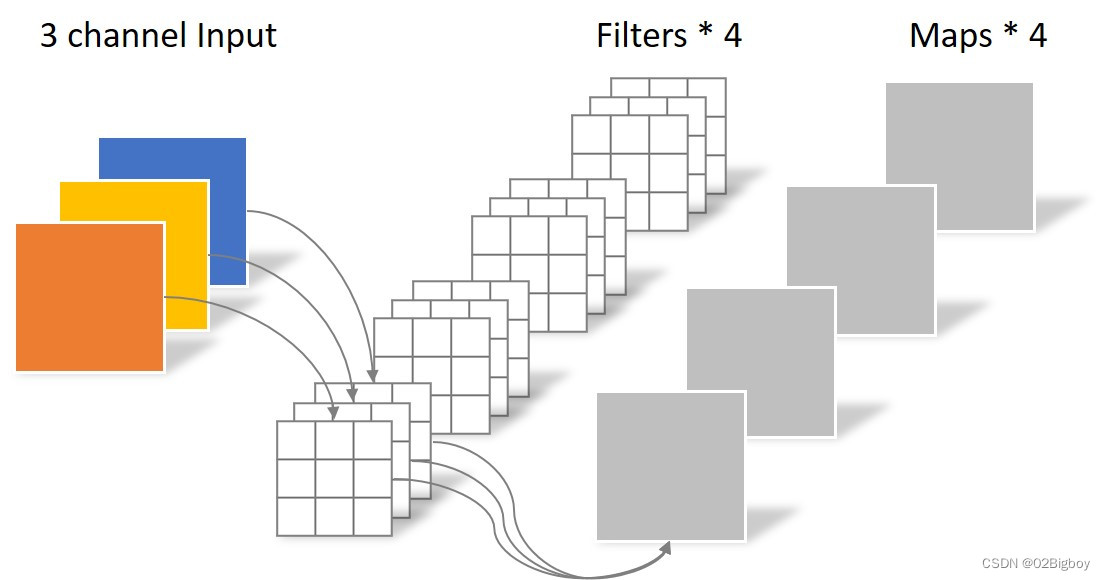
图片来源于:常规卷积.png
卷积后特征大小的计算公式:
w n e w = ( w − k + 2 × p ) s + 1 w_{new} = \frac{(w - k + 2\times p)}{s} +1 wnew=s(w−k+2×p)+1
所以我们选(3,3,4,10,0,1)的卷积就可以了,维度分别对应(kernel_size_h, kernel_size_w, input_channel, output_channel, padding, stride)
import torch.nn as nn
x = x.transpose(0, 2) # 卷积的操作输入样本维度:(batchsize,channel,h,w),由于这里一个样本所以batchsize是1,我们需把channel放在首维。
conv_regular = nn.Conv2d(4, 10 , kernel_size=3, stride = 1)
y_regular = conv_regular(x)
print(y_regular.size())
# 计算卷积参数
num_params_regular = sum(p.numel() for p in conv_regular.parameters())
print('the number of model params: {}'.format(num_params_regular))
# torch.Size([10, 3, 3])
# the number of model params: 370
卷积层参数数量的计算公式:
n u m p a r a m e t e r = k e r n e l s i z e h × k e r n e l s i z e w × i n p u t c h a n n e l × o u t p u t c h a n n e l num_{parameter} = kernelsize_h \times kernelsize_w \times input_{channel} \times output_{channel} numparameter=kernelsizeh×kernelsizew×inputchannel×outputchannel
所以上面的卷积参数为: 3 ∗ 3 ∗ 4 ∗ 10 = 360 3*3*4*10=360 3∗3∗4∗10=360 但通过上面程序得出的参数为370,多了输出通道的个数—10。这是因为卷积核的每次滑动,输入到神经元的计算: f ( x ) + b i a s f(x)+bias f(x)+bias, f ( x ) f(x) f(x)j就表示大小为输出通道为 k e r n e l s i z e h × k e r n e l s i z e w × i n p u t c h a n n e l kernelsize_h \times kernelsize_w \times input_{channel} kernelsizeh×kernelsizew×inputchannel 的卷积核与滑动时重叠的样本点乘再累加。10就是相当于有10个卷积核,每个卷积核有一个偏置,所以根据上面公式计算参数会少output_channel的数量。但通常我们会忽略偏置,直接用上面的公式计算参数量。
卷积层的计算量(乘法)计算公式:
k e r n e l s i z e h × k e r n e l s i z e w × ( h − k e r n e l s i z e h + 1 ) × ( w − k e r n e l s i z e w + 1 ) × i n p u t c h a n n e l × o u t p u t c h a n n e l kernelsize_h \times kernelsize_w \times (h-kernelsize_h+1) \times (w-kernelsize_w+1) \times input_channel \times output_channel kernelsizeh×kernelsizew×(h−kernelsizeh+1)×(w−kernelsizew+1)×inputchannel×outputchannel
所以上面的卷积操作的计算量为: 3 ∗ 3 ∗ ( 5 − 3 + 1 ) ∗ ( 5 − 3 + 1 ) ∗ 4 ∗ 10 = 3240 3*3*(5-3+1)*(5-3+1)*4*10=3240 3∗3∗(5−3+1)∗(5−3+1)∗4∗10=3240
分组卷积
分组的意思就是卷积时将通道进行分组,然后再计算。上面的常规卷积,每个卷积核的大小都是kernelsizekernelsize样本通道,即每个卷积核将样本的所有通道一起计算。示意图理解如下。
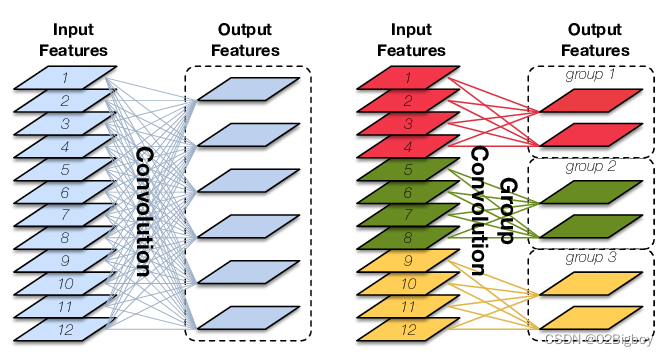
图片来源于: 分组卷积.png.
卷积后最终的(h,w,channel)都与上面常规的卷积一样。只是内部会先对通道进行分组,然后再进行常规的卷积,然后再将结果拼接起来。代码也很好实现,就在后面加一个“groups”参数就行了。
conv_group = nn.Conv2d(4, 10 , kernel_size=3, stride = 1, groups=2)
y_group = conv_group(x)
print(y_group.size())
num_params_regular = sum(p.numel() for p in conv_group.parameters())
print('the number of group conv params: {}'.format(num_params_regular))
# torch.Size([10, 3, 3])
# the number of group conv params: 190
分组卷积层参数数量的计算公式:
n u m p a r a m e t e r = k e r n e l s i z e h × k e r n e l s i z e w × i n p u t c h a n n e l g r o u p s × o u t p u t c h a n n e l g r o u p s × g r o u p s num_{parameter} = kernelsize_h \times kernelsize_w \times \frac{input_{channel}}{groups} \times \frac{output_{channel}}{groups} \times groups numparameter=kernelsizeh×kernelsizew×groupsinputchannel×groupsoutputchannel×groups
所以上面分组卷积参数为: 3 ∗ 3 ∗ 4 / 2 ∗ 10 / 2 ∗ 2 = 180 3*3*4/2*10/2*2=180 3∗3∗4/2∗10/2∗2=180,也和上面一样会多output_channel个偏置。
分组卷积层的计算量(乘法)计算公式:
k e r n e l s i z e h × k e r n e l s i z e w × ( h − k e r n e l s i z e h + 1 ) × ( w − k e r n e l s i z e w + 1 ) × i n p u t c h a n n e l g r o u p s × o u t p u t c h a n n e l g r o u p s × g r o u p s kernelsize_h \times kernelsize_w \times (h-kernelsize_h+1) \times (w-kernelsize_w+1) \times \frac{input_{channel}}{groups} \times \frac{output_{channel}}{groups} \times groups kernelsizeh×kernelsizew×(h−kernelsizeh+1)×(w−kernelsizew+1)×groupsinputchannel×groupsoutputchannel×groups
所以上面分组卷积的计算量为: 3 ∗ 3 ∗ ( 5 − 3 + 1 ) ∗ ( 5 − 3 + 1 ) ∗ 4 / 2 ∗ 10 / 2 ∗ 2 = 1620 3*3*(5-3+1)*(5-3+1)*4/2*10/2*2=1620 3∗3∗(5−3+1)∗(5−3+1)∗4/2∗10/2∗2=1620
所以可以看出分组卷积能在输出维度一样的情况下,使得网络参数更少,计算量也更少-----参数和计算量都相当于除了组数。
但分组卷积存在问题:组与组通道之间信息不流通。
解决的办法可以是在叠卷积层时,不同层用不同的组数,如交替使用2,3的组数。
深度分离卷积
深度分离卷积由两部分组成:
逐通道卷积(depthwise conv)
逐通道卷积时分组卷积的一个特例:input_channel = output_channel = groups, 分组数等于输入通道数等于输出通道数。
便于理解,示意图如下图所示。
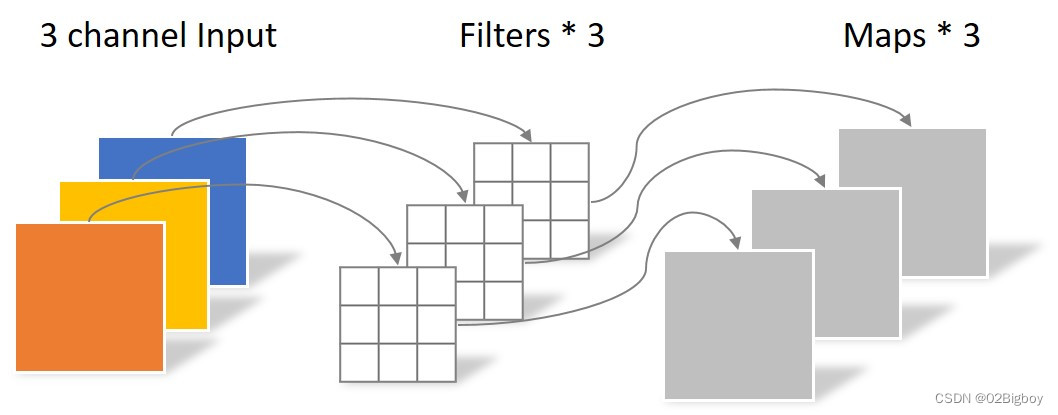
图片来源于: 逐通道卷积.png
样本通过4通道的逐通道卷积:
conv_depthwise = nn.Conv2d(4, 4 , kernel_size=3, stride = 1, groups=4)
y_depthwise = conv_depthwise(x)
print(y_depthwise.size())
num_params_regular = sum(p.numel() for p in conv_depthwise.parameters())
print('the number of depthwise conv params: {}'.format(num_params_regular))
# torch.Size([4, 3, 3])
# the number of depthwise conv params: 40
可见 样本大小是我们期望的大小,只是通道数和原来一样,所以这只是深度分离卷积的第一步----逐深度卷积。
由于这是分层卷积的一个特例,所以我们带入分层卷积的参数计算公式可得,这里逐层卷积参数为: 3 ∗ 3 ∗ 1 ∗ 1 ∗ 4 = 36 3*3*1*1*4=36 3∗3∗1∗1∗4=36 然后再加4个卷积核的偏置。
计算量: 3 ∗ 3 ∗ ( 5 − 3 + 1 ) ∗ ( 5 − 3 + 1 ) ∗ 1 ∗ 1 ∗ 4 = 320 3*3*(5-3+1)*(5-3+1)*1*1*4=320 3∗3∗(5−3+1)∗(5−3+1)∗1∗1∗4=320
逐点卷积 (pointwise conv)
用kernel_size=1的卷积,只改变特征的通道数,实现了深度方向的加权组合----弥补了第一步逐通道卷积时通道分组导致信息在通道之间不流通的缺点。
为便于理解,逐点卷积的示意图如下。
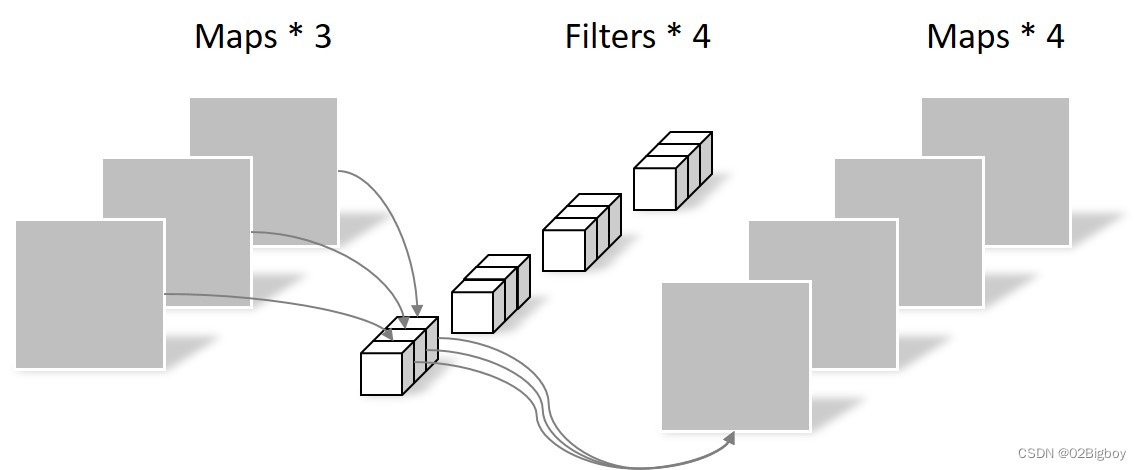
图片来源于:逐点卷积.png
conv_pointwise = nn.Conv2d(4, 10 , kernel_size=1, stride = 1)
y_pointwise = conv_pointwise(y_depthwise)
print(y_pointwise.size())
num_params_regular = sum(p.numel() for p in conv_pointwise.parameters())
print('the number of pointwise conv params: {}'.format(num_params_regular))
# torch.Size([10, 3, 3])
# the number of pointwise conv params: 50
逐点卷积可以看成kernel_size=1的常规的卷积,所以上面的卷积的参数量: 1 ∗ 1 ∗ 4 ∗ 10 = 40 1*1*4*10=40 1∗1∗4∗10=40 ,然后加10个卷积核的偏置。
计算量: 1 ∗ 1 ∗ ( 3 − 1 + 1 ) ∗ ( 3 − 1 + 1 ) ∗ 4 ∗ 10 = 360 1*1*(3-1+1)*(3-1+1)*4*10=360 1∗1∗(3−1+1)∗(3−1+1)∗4∗10=360
深度分离卷积就是逐通道卷积和逐点卷积的组合。即先进行逐通道卷积,将大小(h,w)满足目标,然后又通过逐点卷积将通道(c)满足目标。
从上面分析可得出深度分离卷积的参数量: 40 + 50 = 90 40+50=90 40+50=90
计算量为: 320 + 360 = 680 320+360=680 320+360=680
可见相对于分组卷积,深度分离卷积的参数和计算量进一步减小。
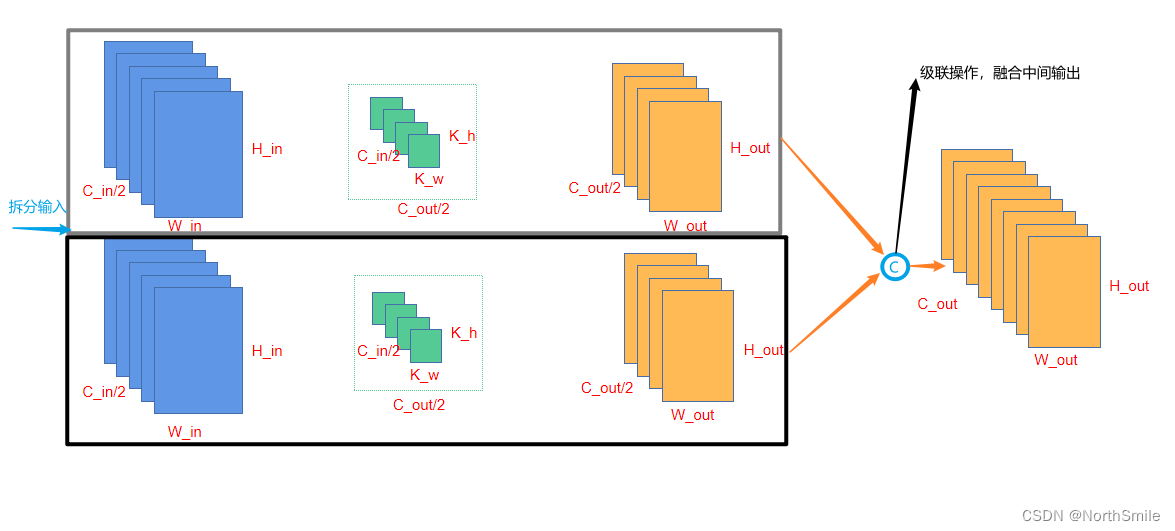
分组深度分离卷积
这个的意思就是先通道进行分组,然后再每组上做深度分离卷积。这样参数和计算量会进一步减小。
为便于理解,示意图如下。
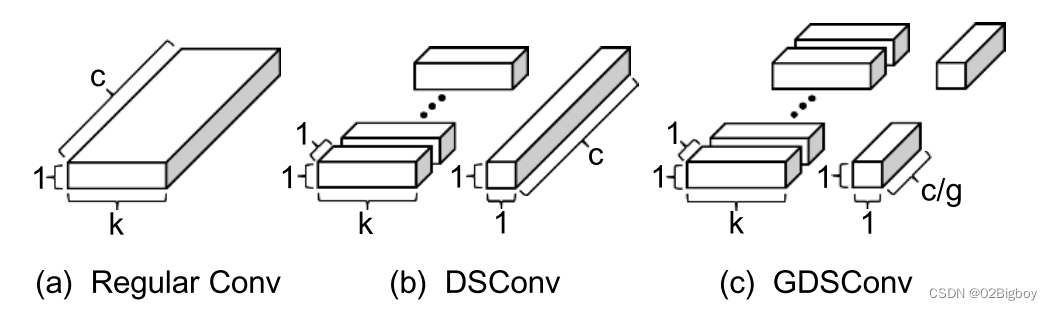
图片来源于:论文:SMALL-FOOTPRINT KEYWORD SPOTTING ON RAWAUDIO DATA WITH SINC-CONVOLUTIONS
import torch.nn as nn
import torch.nn.functional as F
group = 2
input_channel = 4
output_channel = 10
conv_GDSconv = nn.ModuleList()
group_in_channel = int(input_channel/group) # 分组注意整除,这里我只考虑了简单情况,没有完善。
group_out_channel = int(output_channel/group)
for i in range(group):i_groupp = nn.Sequential(nn.Conv2d(group_in_channel,group_in_channel,3,stride=1,groups=group_in_channel), nn.Conv2d(group_in_channel, group_out_channel, kernel_size=1, stride=1),)conv_GDSconv.append(i_groupp)
i_c = 0
y_group = []
for block in conv_GDSconv:y_block = block(x[i_c:i_c+group_in_channel,:,:]) # 将x分组,然后每组做深度分离卷积y_group.append(y_block)i_c +=group_in_channel
y_GDSconv = torch.cat(y_group, dim=0)
print(y_GDSconv.size())
num_params_regular = sum(p.numel() for p in conv_GDSconv.parameters())
print('the number of GDS conv params: {}'.format(num_params_regular))
# torch.Size([10, 3, 3])
# the number of GDS conv params: 70
上面代码是分组数为2的分组深度分离卷积。
参数计算量:两组的深度分离卷积,即两组 ( 5 , 5 , 4 / 2 ) → ( 3 , 3 , 10 / 2 ) (5,5,4/2)\rightarrow (3,3,10/2) (5,5,4/2)→(3,3,10/2)的深度分离卷积的变换。
每一组的参数: 3 ∗ 3 ∗ 1 ∗ 1 ∗ 2 + 2 ( b i a s ) + 1 ∗ 1 ∗ 4 / 2 ∗ 10 / 2 + 5 ( b i a s ) = 35 3*3*1*1*2 + 2(bias) + 1*1*4/2*10/2 + 5(bias) = 35 3∗3∗1∗1∗2+2(bias)+1∗1∗4/2∗10/2+5(bias)=35,所以总的参数为70。
计算量:
每一组计算量: 3 ∗ 3 ∗ ( 5 − 3 + 1 ) ∗ ( 5 − 3 + 1 ) ∗ 1 ∗ 1 ∗ 2 + 1 ∗ 1 ∗ ( 3 − 1 + 1 ) ∗ ( 3 − 1 + 1 ) ∗ 4 / 2 ∗ 10 / 2 = 252 3∗3∗(5−3+1)∗(5−3+1)∗1∗1∗2 + 1*1*(3-1+1)*(3-1+1)*4/2*10/2 = 252 3∗3∗(5−3+1)∗(5−3+1)∗1∗1∗2+1∗1∗(3−1+1)∗(3−1+1)∗4/2∗10/2=252,所以总的参数量:504
上面卷积总结
( 5 , 5 , 4 ) → ( 3 , 3 , 10 ) (5,5,4)\rightarrow (3,3,10) (5,5,4)→(3,3,10)的卷积实例而言:
| 卷积 | 参数量 | 计算量 |
|---|---|---|
| 常规卷积 | 370 | 3240 |
| 分组卷积 | 190 | 1620 |
| 深度分离卷积 | 90 | 680 |
| 分组深度分离卷积 | 70 | 504 |
卷积的dilation
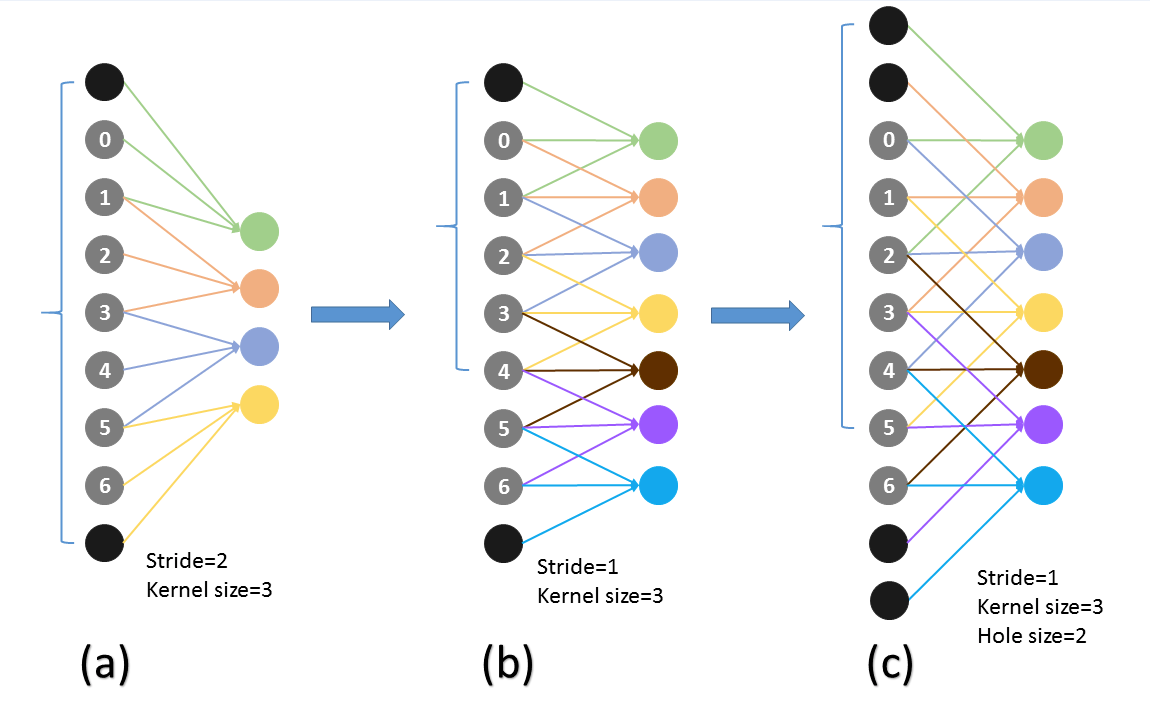
为了便于理解,dilation卷积的示意图如下:
 图1 常规的卷积 图1 常规的卷积 | 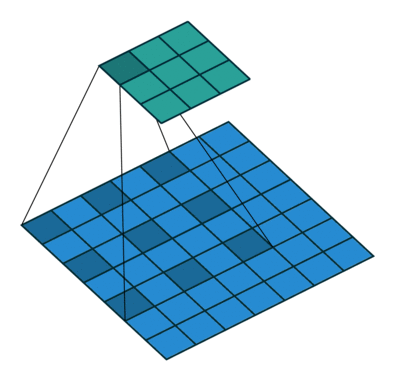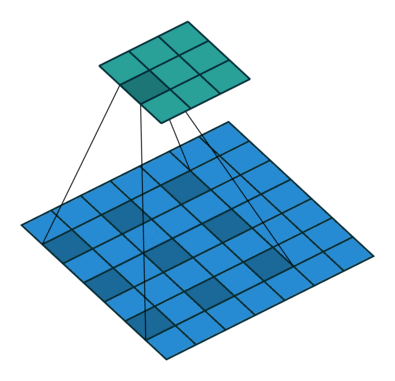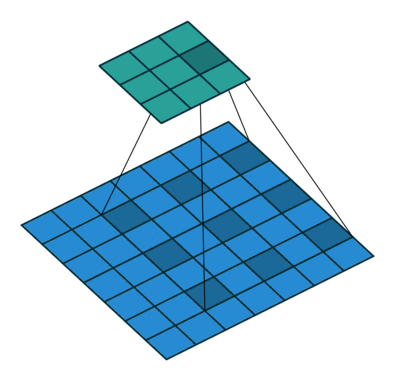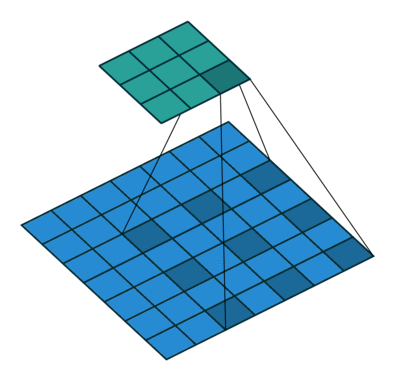 图2 dilation=2的卷积 图2 dilation=2的卷积 |
图片来源于:卷积.gif
一般卷积的默认dilation=1, 当我们改变dilation的值后,就会两两卷积点中插入(dilation-1)的空白,如上图所示dilation=2。
用dilation后特征大小的计算公式:
w d i l a t i o n = ( w − d i a l a t i o n × ( k − 1 ) − 1 + 2 × p ) s + 1 w_{dilation} = \frac{(w - dialation\times (k-1) -1 + 2\times p)}{s} +1 wdilation=s(w−dialation×(k−1)−1+2×p)+1
即用了dilation后新的kernel_size= d i a l a t i o n × ( k − 1 ) + 1 dialation\times (k-1) +1 dialation×(k−1)+1 引用
conv_dilation = nn.Conv2d(4, 10 , kernel_size=3, stride = 1, dilation=2)
y_dilation = conv_dilation(x)
print(y_dilation.size())
num_params_regular = sum(p.numel() for p in conv_dilation.parameters())
print('the number of dilation conv params: {}'.format(num_params_regular))
# torch.Size([10, 1, 1])
# the number of dilation conv params: 370
dilation的作用一般是可以在相同参数下增大卷积的感受野。
dilatio卷积的感受野计算公式:
r e c e p t i v e f i l e d = ∑ i d i × ( k i − 1 ) receptive_{filed} = \sum_i{d_i\times(k_i-1)} receptivefiled=i∑di×(ki−1)
公式来源于:论文:EFFICIENT KEYWORD SPOTTING USING DILATED CONVOLUTIONS AND GATING
其中, d i , k i d_i,k_i di,ki分别表示第i层的dilation的值,和第i层的卷积核的值。