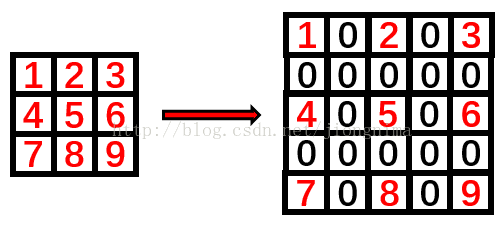最近工作要用到dilation conv，在此总结一下空洞卷积，并和deconv进行对比。

dilation conv

首先空洞卷积的目的是为了在扩大感受野的同时，不降低图片分辨率和不引入额外参数及计算量（一般在CNN中扩大感受野都需要使用s>1的conv或者pooling，导致分辨率降低，不利于segmentation。如果使用大卷积核，确实可以达到增大感受野，但是会引入额外的参数及计算量）。

知乎上关于空洞卷积的前两个回答比较不错，可以参考借鉴。 如何理解空洞卷积（dilated convolution）？

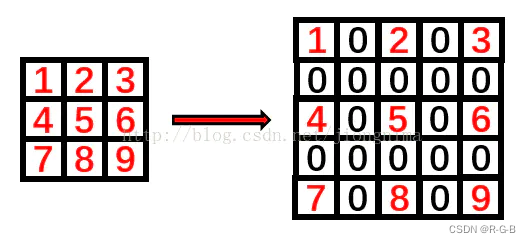
空洞卷积的feature map size计算：对于K*K的卷积核，rate =r，则扩充后的卷积核size = K+(K-1)*(r-1)。rate可以理解为K*K的卷积核上的一像素点旁边第rate个点是原K*K的卷积核邻近的点，也相当于K*K的卷积核中两个相邻的点中间插入了r-1个点。特别地，对于3*3的卷积核，如果pad = rate，则特征图尺寸大小不改变。

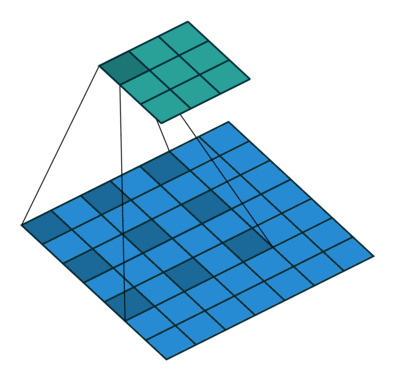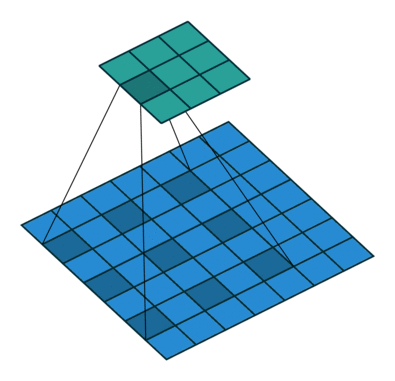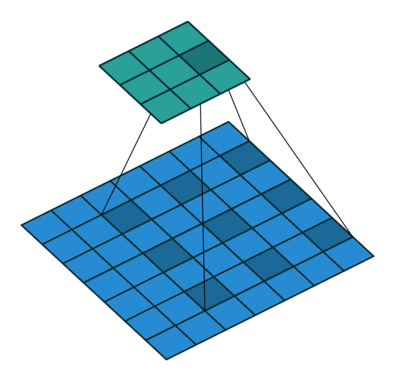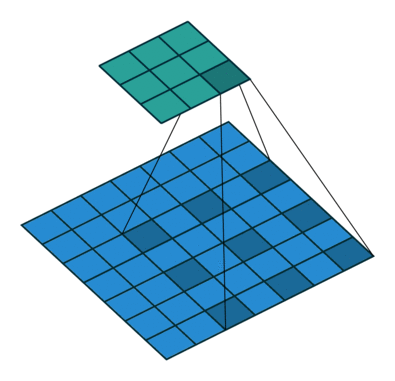
不同rate的空洞卷积组合，具体的感受野如何获得呢？例如rate =1的3*3卷积（就是普通卷积），后接rate=2的3*3卷积，感受野是7*7.一种理解方法是rate=2的3*3卷积其实相当于5*5卷积，3*3和5*5叠加自然是7*7卷积，总结一个一般性的结论， 对于s=1, a*a的常规卷积和b*b的常规卷积组合相当于（a+b-1）的卷积核（可以从平移的角度思考，参考下图）。从下图中也可以看出，最下面的表示原图，1*1卷积依次在原图上以s=1进行卷积（s一般为1，如果不为1，就会改变特征图尺寸，空洞卷积也就失去作用）得到不同颜色的块，如右边的一行块所示。在这上面进行rate=2的3*3卷积，可以看到每次卷积会用到红色，黄色，绿色三个块，对应到原图紫色区域，刚好是7*7.

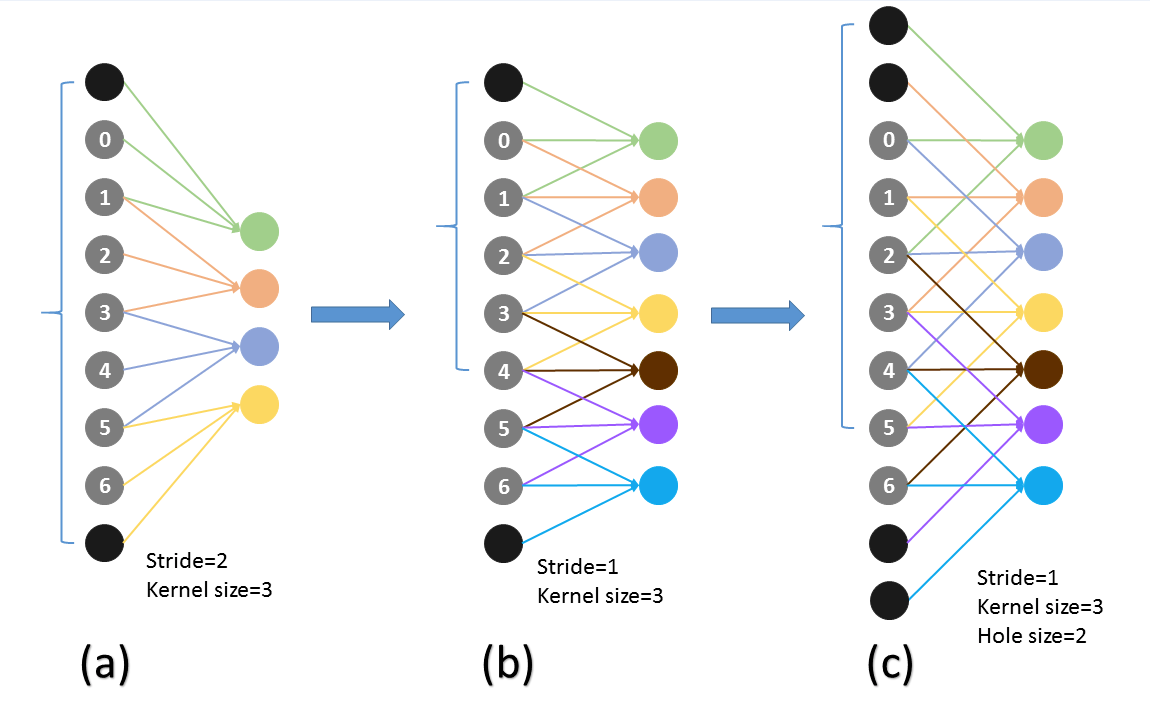
空洞卷积一般应用在segmentation，对于detection也有很大的用处，使用的时候，如果一直使用同一个rate的空洞卷积或者rate存在公约数就会出现 The Gridding Effect问题，简单来说就是一直使用了底层特征图的部分像素点，而忽略了很大一部分像素点。

如下图所示，最上面表示bottom层使用rate=2的空洞卷积，从下面三种情况可以看出，使用2+3或者2+5就不会出现白色的像素点没用上的情况。

这个问题在图森的文章里面提到过，Understanding Convolution for Semantic Segmentation

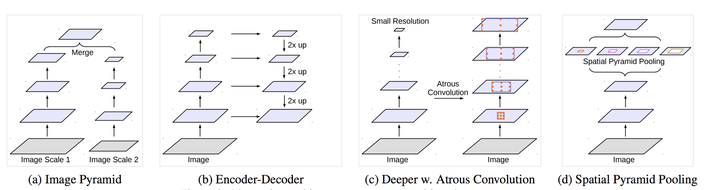
HDC把rate设成锯齿状。DUC用于上采样。这从侧面说明了ASPP的改进地方，ASPP用了平行的几个空洞卷积（rate=6,12,18,24等）。

deconv

转置卷积多数用于上采样。转置怎么理解呢？对于一个[3,3]的input，可以视为[1,9]，欲得到[2,2]的输出，视为[1,4]。则需要一个[4,9]的权重矩阵，反之，如果从[1,4]得到[1,9]，那么需要[9,4]的权重矩阵，也就是之前的转置。个人觉得这只是一个shape的转置，并不是说它的value就是原权重矩阵转置的对应value。 这篇博文关于相关概念的解释比较清楚：deconv

关于实现，参考github，图片不搬过来了，可以对照着打开看。直接看Transposed conv部分。

蓝色部分是输入，绿色部分是输出。

上面一行，s=1。第一个图其实就是标准卷积的逆过程，为什么说没有pading呢，我觉得是为了和标准卷积对应，因为4*4生成2*2不需要pad。后面的half padding其实就是希望输出和输入一样的特征图（关于conv的三种形式：full其实是放大，same是同等输出， valid是downsamping，参考链接），在普通卷积，这样的过程是需要进行pad的，所以此处也写了padding。其实把half padding就是普通卷积的same padding。Arbitrary padding是随机补充，还没太弄懂，有清楚的朋友还望赐教。full padding是希望输出比输入要小，相当于vaild conv，对应于普通卷积的full conv逆过程，所以有了full padding。

下面一行，有了stride. 对应于标准卷积的s<1.在map中间插入0像素点（不同于dilation conv是skip掉一些像素点），接下来就转化成了s=1的卷积。至于为什么第一张图实际上还是有padding，我是这么理解的：因为填充了0像素点后还不能达到输出，所以就和no stride一样的做法，2*2插完值后变成3*3.但是要想输出为5*5，在s=1的情况下，必须要进行p=2。对应于正向的5*5输出3*3不需要padding，所以此处对应也不用padding.最后一张图，加了个odd，其实这是一个填充，目的为了让所有的map上的点都能用到（图中对应蓝色最右边一列）。参考链接

总结起来，deconv中的padding是和conv的padding对应，并不是说deconv的padding=0，就真的没有填充；s<1时，先把map中的每个点插入部分0像素（和s有关），然后变成s=1的deconv. odd不是新概念，主要是为了充分利用map上的像素值。

总起来说，dilation conv是对卷积核进行upsample，deconv是对feature map进行upsample；或者说，dilation conv是skip掉map中的一些元素，而deconv是对map中的元素进行补0操作。